Розв'язування лінійних рівнянь з однією змінною
Тема. Розв'язування лінійних рівнянь з однією змінною
Мета: сформувати уявлення про зміст поняття «лінійне рівняння з однією змінною» та способи його розв'язування; відпрацювати навички розв'язування рівнянь, що зводяться до лінійних.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
- Проводимо вибірково, взявши в декількох учнів зошити для перевірки.
- Для діагностики рівня засвоєння властивостей (рівносильності) рівнянь проводимо невелику самостійну роботу, яку перевіряємо одразу по закінченні.
Самостійна робота
Розв'яжіть рівняння:
Варіант 1 [2]
а) 7х + 3 = 30 - 2х; б) ![]() х + 15 =
х + 15 = ![]() х + 10; в) 0,3(х - 2) = 0,2х + 2
х + 10; в) 0,3(х - 2) = 0,2х + 2
[а) 8х – 8 = 20 - 6х; б) ![]() х + 16 =
х + 16 = ![]() х + 9; в) 2,7 + 3y = 9(y – 2,1)]
х + 9; в) 2,7 + 3y = 9(y – 2,1)]
III. Відтворення знань
Під час перевірки правильності виконання самостійної роботи учні повторюють та відтворюють свої знання щодо:
а) властивостей рівнянь;
б) алгоритму розв'язування рівнянь;
в) правил виконання арифметичних дій з раціональними числами та
властивостями цих дій.
IV. Формування знань
По суті єдиним новим поняттям уроку є поняття лінійного рівняння з однією змінною; на інтуїтивному рівні учні це поняття вже засвоїли (згадаймо алгоритм розв'язування рівнянь, розглянутий на попередньому уроці). Тому просто повертаємось до розв'язаних прикладів і звертаємо увагу на те, що всі розв'язані досі рівняння приводили до вигляду ах = b, де а та b — деякі числа. Такі рівняння ми будемо називати лінійними рівняннями з однією змінною.
Зауважимо, що іноді лінійними рівняннями з однією змінною називають і такі рівняння, які можна привести до вигляду ах = b, виконавши спрощення виразів у правій та лівій частинах рівняння та зробивши перенесення доданків з однієї частини рівняння в іншу.
Також важливо наголосити на тому, що при а ≠ 0 лінійне рівняння обов'язково має раціональний корінь, тобто коренем є число, що може бути записане у вигляді ![]() . Тому під час розв'язування рівнянь вигляду ах = b, де а ≠ 0, краще х записати як
. Тому під час розв'язування рівнянь вигляду ах = b, де а ≠ 0, краще х записати як ![]() , а потім вже перетворювати цей вираз (а не ділити b на а «куточком», бо часто-густо матимемо нескінченний періодичний дріб).
, а потім вже перетворювати цей вираз (а не ділити b на а «куточком», бо часто-густо матимемо нескінченний періодичний дріб).
V. Закріплення знань. Відпрацювання навичок
Усні вправи
- Які з рівнянь є лінійними?
а) 3х = 6; б) -3х = 5; в) -3х = 0; г) -![]() = 0; д) -
= 0; д) -![]() = 0.
= 0.
- Розв'яжіть лінійне рівняння:
а) 3х = 6; б) -3х = 6; в) -![]() = 6; г) -
= 6; г) -![]() = 0; д) * + 0х = 6; е) * 0х = 0.
= 0; д) * + 0х = 6; е) * 0х = 0.
Оскільки схема розв'язування лінійного рівняння з однією змінною при будь-яких значеннях а та b дається в 7 класі, на цьому етапі ми розглядаємо в основному випадки, коли а ≠ 0, а інші можливі випадки лише на інтуїтивному рівні (для сильних, підготовлених класів).
Письмові вправи
- Розв'яжіть рівняння:
а) 0,5х + 3 = 0,2х; б) -0,4а – 14 = 0,3a; в) 2х - 6![]() =
= ![]() x + 7
x + 7![]() ;
;
г) 6,9 – 9a = -5a - 33,1; д) ![]() k - 12,5 =
k - 12,5 = ![]() k -
k - ![]() ; є) 4,7 – 8z = 4,9 – 10z;
; є) 4,7 – 8z = 4,9 – 10z;
ж) 7,3а = 1,6а; з) -19t = 11t; к) 3(4х – 8) = 3х - 6;
л) -3,2x + 4,8 = -2 · (1,2х + 2,4); м) -5 · (0,8z – 1,2) = z + 1,2;
н) ![]() ·
· = 4х + 2
= 4х + 2![]() .
.
-
Знайдіть значення виразу
 .
.
VI. Підсумок уроку
Яке рівняння називають лінійним з однією змінною? Наведіть приклад лінійного рівняння з однією змінною, корінь якого дорівнює:
а) 1; б) -2; в) 0; г) будь-якому числу.
VII. Домашнє завдання
- Розв'яжіть рівняння:
а) 4(х - 6) = х - 9; б) 6 - 3(х + 1) = 7 - х; в) (8х + 3) - (10х + 6) = 9;
г) 2,8 – х = 8(х + 2,8); д) 0,3(6 – 3y) = 4,5 - 0,8(y – 9);
є) ![]() ; ж)
; ж) ![]() x + 14 =
x + 14 = ![]() x + 9.
x + 9.
-
Знайдіть значення виразу
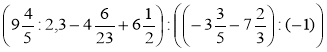 .
.


про публікацію авторської розробки
Додати розробку
