Розподільна властивість множення. Зведення подібних доданків.
Тема. Розподільна властивість множення. Зведення подібних доданків.
Мета: використовуючи знання про способи використання розподільної властивості множення, виробити вміння:
а) знаходити подібні доданки та визначати з алгебраїчної суми їх коефіцієнти;
б) виконувати зведення подібних доданків.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
Математичний диктант
Варіант 1 [2]
- Запишіть вираз та обчисліть його значення:
577 · 58 + 423 · 58 [76,8 · 9,5 - 66,8 · 9,5];
34,2 · 91,3 - 24,2 · 91,3 [718 · 34 + 282 · 34].
-
Запишіть вираз та обчисліть його значення: 6 ·
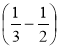
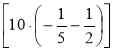 .
.
-
Подавши один з множників у вигляді суми розрядної одиниці та числа
±1, обчисліть усно значення добутку -999 · 17 [-12 · 9999].
II. Актуалізація опорних знань
Під час перевірки правильності розв'язання завдань математичного диктанту учні повторюють самі формулювання розподільної властивості та способи її застосування (для розкриття дужок та винесення спільного множника за дужки).
Звернувшись до конспекту, записаного на попередньому уроці, учні розуміють, що основнім матеріалом уроку є робота з буквеними виразами.
III. Доповнення знань
Щоб мати чіткі уявлення про зміст понять «подібні доданки» та «зведення подібних доданків», ми формулюємо відповідні означення та показуємо на прикладах їх зміст.
IV. Вироблення вмінь
Звернемо увагу на такі моменти:
а) щоб звести подібні доданки, треба правильно визначити їх коефіцієнти (а для цього згадуємо про алгебраїчну суму), а потім вже додавати ці коефіцієнти; під час зведення подібних доданків буквена частина не змінюється;
б) у виразі може бути не одна, а кілька груп подібних доданків. У цьому випадку спочатку окремо виділяємо кожну групу (традиційно підкреслюємо певною кількістю рисок кожну групу подібних доданків), а потім уже для кожної групи подібних доданків повторюємо п. а);
в) якщо даний вираз містить дужки, то перш ніж звести подібні доданки (тобто виконати додавання), треба розкрити дужки (тобто виконати множення, використовуючи або розподільну властивість, або правила), а потім уже дивись п. а) чи б);
г) якщо в алгебраїчній сумі є кілька (більше від одного) числових доданків, то їх також можна вважати подібними доданками (і не забуваймо їх додавати).
Усні вправи
Зведіть подібні доданки у виразі:
а) 5х - 4х; б) 4а – а; в) 5х - 7х; г) 4а – 5а + а.
Письмові вправи
- Зведіть подібні доданки:
а) 9a – 13a + 2a; б) 5a - 6a + 2a - 10a; в) -9х + 7х - 5х + 2х;
г) 2,8b – b + 2,8b - b; д) -4х – 7 – 5х + 10х; e) 5a + b – 7b + 3a;
ж) -7а + 5а – х – 6х; з) 12х – 11 + 4а – 7х; и) 8а – 9х + 4 – а + х.
Записи в зошитах можуть мати такий вигляд:
а) 9а – 13а + 2а = (9 – 13 + 2) а = -2а;
є) 5a + b - 7b + 3a = (5 + 3)a + (1 – 7)b = 8a + (-6)b = 8a - 6b i т. д.
- Розкрийте дужки:
а) (х – у) · 5; б) (а + b – с) · 4; в) (2х – у) · (-3); г) -2a(b + 2с – 3m);
д) -a(6b - 5c); е)(-а + 3b + с)(-2х).
- Спростіть вираз:
а) 3(-2х + 5) + 4(х – 2); б) -(2а – 3) - 2(3а – 1); в) -5(-3х + 2) - (9 - х);
г) (3b - 1) · (-5) + (4 + b) · (-2).
- Спростіть вираз:
а) 0,7х - 0,9х + ![]() х; б) -
х; б) -![]() b + 1
b + 1![]() b -
b - ![]() b; в)
b; в) ![]() а +
а + ![]() b – b + 0,4a;
b – b + 0,4a;
г) -7(а – 2b + 2) + (5а – 5) · (-2); д) а(3х - 2у + 5) – 2а(-2х - у);
є) -6![]() + 4а + 7b.
+ 4а + 7b.
Додаткові вправи
-
Один робітник може виконати замовлення за 6 днів, а другий — за
15 днів. Спочатку 2 дні над замовленням працював перший робітник,
а потім закінчив другий. Скільки днів працював другий робітник? - Знайдіть значення виразу:
а) (3х)2, якщо х = 2; -2; б) а3 – 12, якщо а = -2; 3.
IV. Підсумки уроку
Заповніть пропуски:
а) 5a – 3a = ...; б) 5a - 3a + b = …; в) 5a - 3a + b - 2b = ...;
г) 5(a + b) - 3a = ..; д) 5(a + b) - (a - b) = …
VI. Домашнє завдання
Усні вправи
- Назвіть подібні доданки у виразах:
а) х - 2у + 3х - у; б) 7b - a - 2ab + b - 3ab.
-
Зведіть подібні доданки: а) 5х - 4х; б) 4а - а; в) 5х - 7х; г) 4а - 5а + а.
Письмові вправи
-
Розкрийте дужки: а) 3(а - с); б) -6(2а + b); в) (-4а – 3b) · 5; г) а(3b - 4с);
д) (x + y - z) · (-a); e) -5a(-2b + 4c - d). - Зведіть подібні доданки:
а) 3с + 7с - 8с; б) 16а – 5а + 7а – 11а; в) -4t + 3t – 8 – 7t;
г) 8x – 8y + 2y - 6x; д) 4,5a - 7b - 1,5a + 1; e) –a + 3b - 4b + 1,5a.
- Спростіть вираз: а) (5х - 3) · 2 – 5(3 – 2х); б) -(3а – 2) + 5(а – 2).
- Один екскаватор може вирити траншею за 9 год, а другий цю ж траншею — за 6 год. Яку частину траншеї вириють екскаватори за 3 год спільної роботи?


про публікацію авторської розробки
Додати розробку
