Розподільна властивість множення. Зведення подібних доданків
Тема. Розподільна властивість множення. Зведення подібних доданків
Мета: завершити роботу з відпрацювання навичок використання розподільної властивості множення для: а) обчислень; б) розкриття дужок; в) зведення подібних доданків; г) винесення найбільшого спільного множника за дужки.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
Усні вправи
- Обчисліть, використовуючи розподільну властивість множення:
а) 4![]() · 5; б) 2
· 5; б) 2![]() · (-3); в) (-8) ·
· (-3); в) (-8) · ![]() ; г) -18,6 · 8
; г) -18,6 · 8![]() + 1
+ 1![]() · (-18,6);
· (-18,6);
д) 5,27 · (-15) - (-15) · (-4,73); є) 5![]() ·
· ![]() -
- ![]() ·
· ![]() .
.
-
Спростіть вираз: а) 31а + 14а; б) 34х + 15х; в) 29b – b; г) 45у – у;
д) х + 34х; е) а + 23а; ж) 2а – 3b + а.
II. Відтворення знань
Запитання до класу
- Які доданки називають подібними?
- Чим можуть відрізнятися один від одного подібні доданки?
- Що означає «звести подібні доданки»? Як звести подібні доданки?
-
Які властивості множення використовуємо, щоб спростити вираз
4(a + b) – 0,5(a – b)?
ІІІ. Відпрацювання навичок
На ньому, третьому в темі «Розподільна властивість множення» уроці, ми завершуємо роботу з відпрацювання навичок застосування розподільної властивості множення для спрощення обчислень значень числових виразів та спрощення буквених виразів та винесення спільного множника за дужки. Також у кінці уроку пропонуємо самостійну роботу.
- Розв'яжіть рівняння:
а) 3х + 2 – х = 6; б) 3(х – 1) – х = 0; в) 7 – 3у + 4у – 4 = -1.
- Винесіть за дужки спільний множник:
а) 7х + 7у; б) 15х – 10у; в) 10т - тk; г) 16a + 8ab;
д) 4ab + 6ac; є) 3та – 6тb – 6тс.
-
Винесіть за дужки спільний множник:
a) 54xy – 62xz; б) 10ab – 15bc – 25b; в) 42ах – 70ay – 84az. - Обчисліть найзручнішим способом:
а) -0,2 · 3,8 - 3, 7 · (-0,2); б) ![]() .
.
- Спростіть вираз, використовуючи розподільну властивість множення:
а) 2(х - 7у + 3z); б) -![]() х +
х + ![]() х -
х - ![]() х – х + с; в) 0,6(4х – 12) – 0,4(5х – 7).
х – х + с; в) 0,6(4х – 12) – 0,4(5х – 7).
IV. Діагностика рівня засвоєння навчального матеріалу Тестові завдання
Варіант 1
- Який результат дістанемо, застосувавши розподільний закон множення для обчислення виразу (0,03 + 2,5) · 0,4?
1) 1,12; 2) 10,12; 3) 1,012; 4) 2,12.
- Який вираз дістанемо, розкривши дужки в добутку -5р(-х + 2у – 3k)?
1) -5хр + 10ру - 15рк; 2) 5рх - 10ру +15рк;
3) 5рх - 10рх - 15рк; 4) 5рх -2ру + 15рк.
-
Який вираз дістанемо, спростивши вираз 4с(3а – 2) – 6а(2с + 1)?
1) 12aс – 8с + 12ас + 6a; 2) -8с - 6а; 3) -8с + 6a; 4) 8с - 6а. -
Обчисліть значення виразу 5·(5p – 4х) – 4·(х – 2p), якщо p = -2; х = 2.
1) -18; 2) -114; 3) -90; 4) 90. -
Укажіть корінь рівняння -5·(у – 2) + 3(2 – у) = 0:
1) 8; 2) -2; 3) 2; 4) -0,25.
Варіант 2
-
Яке з поданих чисел дістанемо, застосувавши розподільний закон
множення до виразу (12,5 + 0,1) · 0,8?
1) 100,8; 2) 18; 3) 10,8; 4) 10,08.
-
Який вираз дістанемо, розкривши дужки в добутку -2k(3а – 5b – 2с)?
1) 6ak - 10bk – 4ck; 2) 6ак +10bk + 4ck;
3) -6ak + 10bk + 4ck; 4) -3аk – 5bk – 4сk.
-
Який вираз дістанемо, спростивши вираз 5p · (-3 + k) – k · (5p – 1)?
1) -15p - k; 2) 15р – k; 3) -15р + k; 4) -15р + 5рk + 5рk – k. -
Обчисліть значення виразу (2х - 3у) – 2·(5х - 2у), якщо х = -1, у = 1?
1) -9; 2) 1; 3) 9; 4) -1. - Знайдіть корінь рівняння (х – 1) – 2(1 – х) = 12:
1) 3; 2) 9; 3) 5; 4) -3.
IV. Підбиваємо підсумки уроку, перевіряючи якість виконання завдань тестової роботи
V. Домашнє завдання
- Розв'яжіть рівняння: а) 7х – 3 – 6х + 3 = -5, б) 4(х – 5) – 3х + 6 = -2.
- Спростіть вираз і знайдіть його значення:
а) -5(с + 2) - (2с – 3), якщо с = 1,5;
б) 4х - 3а - 5х + 4а, якщо а = -0,27, х = 0,07.
-
Спростіть вираз: а) 1
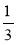 а -
а - 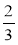 а – а; б)
а – а; б) 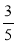 b +
b + 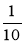 b -
b - 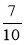 b;
b;
в) (2х – у – 3) · (-2) – 2(2х – у); г) 2x(-3b + 5c) – x(2a – 4b).
- Знайдіть добуток цілих розв'язків нерівності:
а) -7 ≤ х ≤ -1; б) -3 ≤ х < 2; в) -7![]() ≤ х < -1.
≤ х < -1.


про публікацію авторської розробки
Додати розробку
