розробка матеріалів щодо повторення навчального матеріалу в 11 класі

Пояснювальна записка

Основною метою створення даного календарно-тематичного повторення є узагальнення та систематизація навчального матеріалу, його теоретичної та практичної частини.

Також це є якісна та ґрунтовна підготовка учнів до складання зовнішнього незалежного оцінювання.

Дане календарне планування цілком відповідає чинній програмі зовнішнього незалежного оцінювання. Поділене на основні розділи.

Розділ 1. Числа і вирази.

Учні повинні знати: властивості дій з дійсними числами; правила порівняння дійсних чисел; ознаки подільності натуральних чисел на 2, 3, 5, 9, 10; правила округлення цілих чисел і десяткових дробів; означення кореня n-го степеня та арифметичного кореня n-го степеня; властивості коренів; означення степеня з натуральним, цілим та раціональним показниками, їхні властивості; числові проміжки; модуль дійсного числа та його властивості; відношення, пропорції; основна властивість пропорції; означення відсотка; правила виконання відсоткових розрахунків; означення області допустимих значень змінних виразу зі змінними; означення тотожно рівних виразів, тотожного перетворення виразу, тотожності; означення одночлена та многочлена; правила додавання, віднімання і множення одночленів та многочленів; формули скороченого множення; розклад многочлена на множники; означення алгебраїчного дробу; правило виконання дій з алгебраїчними дробами; означення та властивості логарифма, десятковий і натуральний логарифми; основна логарифмічна тотожність; означення синуса, косинуса, тангенса, котангенса, числового аргументу; основна тригонометрична тотожність та наслідки з неї; формули зведення; формули додавання та наслідки з них.

Під час повторення даного розділу учні сформують наступні предметні вміння та способи навчальної діяльності: розрізняти види чисел та числових проміжків; порівнювати дійсні числа; виконувати дії з дійсними числами; використовувати ознаки подільності; знаходити неповну часту та остачу від ділення одного числа на інше; округлювати цілі числа і десяткові дроби; використовувати властивості модуля до розв’язання задач; знаходити відношення чисел у вигляді відсотку, відсоток від числа, число за значенням його відсотка; виконувати тотожні перетворення раціональних, ірраціональних, степеневих, показникових, логарифмічних, тригонометричних виразів та знаходити їх числове значення при заданих значеннях змінних.

 

Розділ 2. Рівняння, нерівності та їх системи.

Учні повинні знати: рівняння з однією змінною, означення кореня рівняння з однією змінною; нерівність з однією змінною, означення розв’язку нерівності з однією змінною; означення розв’язку системи рівнянь з двома змінними та методи їх розв’язань; рівносильні рівняння,нерівності та їх системи; методи розв’язування раціональних, ірраціональних, показникових, логарифмічних, тригонометричних рівнянь.

Під час повторення даного розділу учні сформують наступні предметні вміння та способи навчальної діяльності: розв’язувати рівняння і нерівності першого та другого степенів, а також рівняння і нерівності, що зводяться до них; розв’язувати системи рівнянь і нерівностей першого і другого степенів, а також ті, що зводяться до них; розв’язувати рівняння і нерівності, що містять степеневі, показникові та тригонометричні вирази; розв’язувати ірраціональні рівняння; застосовувати загальні методи та прийоми у процесі розв’язування рівнянь, нерівностей та систем; користуватися графічним методом; застосовувати рівняння, нерівності та системи до розв’язування текстових задач; розв’язувати рівняння і нерівності, що містять змінну під знаком модуля, та з параметрами.

Розділ 3. Функції.

Учні повинні знати: означення функції, область визначення, область значень функції, графік функції; способи задання функцій, основні властивості та графіки функцій, указаних у назві теми; означення функції, оберненої до заданої; рівняння дотичної до графіка функції в точці; означення похідної функції в точці; фізичний та геометричний зміст похідної; таблиця похідних елементарних функцій; правила знаходження похідної суми, добутку, частки двох функцій; правило знаходження похідної складеної функції; достатня умова зростання(спадання) функції на проміжку; екстремуми функції; означення найбільшого і найменшого значень функції.

Під час повторення даного розділу учні сформують наступні предметні вміння та способи навчальної діяльності: знаходити область визначення, область значень функції; досліджувати на парність(непарність), періодичність функцію; будувати графіки елементарних функцій; встановлювати властивості числових функцій, заданих формулою або графіком; використовувати перетворення графіків функцій; знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в точці; знаходити похідні елементарних функцій; знаходити похідну складеної функції; розв’язувати задачі з використанням геометричного та фізичного змісту похідної; знаходити проміжки монотонності функції; знаходити екстремуми функції, найбільше та найменше значення функції; досліджувати функції за допомогою похідної та будувати їх графіки.

 

Розділ 4. Числові послідовності.

Учні повинні знати: означення арифметичної та геометричної прогресій; формули n-го члена арифметичної та геометричної прогресій; формули суми n перших членів арифметичної та геометричної прогресій; формули суми нескінченної геометричної прогресії зі знаменником |q| < 1.

Під час повторення даного розділу учні сформують наступні предметні вміння та способи навчальної діяльності: розв’язувати задачі на арифметичну та геометричну прогресії.

Розділ 5. Первісна та визначений інтеграл.

Учні повинні знати: означення, таблицю, правила знаходження первісних; формулу Ньютона-Лейбніца.

Під час повторення даного розділу учні сформують наступні предметні вміння та способи навчальної діяльності: знаходити первісну, використовуючи її основні властивості; застосовувати формулу Ньютона-Лейбніца для обчислення визначеного інтеграла; обчислювати площу криволінійної трапеції, розв’язувати найпростіші прикладні задачі, що зводяться до знаходження інтеграла.

Планування

№ з/п	Кількість годин	Назва теми
	21	Розділ 1. Числа і вирази
1	1	Дійсні числа(натуральні, цілі, раціональні та ірраціональні), їх порівняння та дії з ними
2	1	Числові множини та співвідношення між ними
3	1	Правило округлення цілих чисел і десяткових дробів
4	1	Означення кореня n-го степеня та арифметичного кореня n-го степеня
5	1	Властивості коренів
6	1	Означення степеня з натуральним, цілим та раціональним показником, їхні властивості
7	1	Модуль дійсного числа та його властивості
8	1	Відношення та пропорції
9	1	Основна властивість пропорції
10	1	Відсотки. Правила виконання відсоткових розрахунків
11	1	Основні задачі на відсотки
12	1	Раціональні вирази та їхні перетворення
13	1	Ірраціональні вирази та їхні перетворення
14	1	Степеневі вирази та їхні перетворення
15	1	Показникові вирази та їхні перетворення
16	1	Логарифмічні вирази та їхні перетворення
17	1	Тригонометричні вирази та їхні перетворення
18	1	Основна тригонометрична тотожність та наслідки з неї
19	1	Формули зведення
20	1	Формули додавання та наслідки з них
21	1	Формули подвійного аргументу
	24	Розділ 2. Рівняння, нерівності та їх системи
22	1	Лінійні рівняння
23	1	Квадратні рівняння
24	1	Раціональні рівняння
25	1	Ірраціональні рівняння
26	1	Показникові рівняння
27	1	Логарифмічні рівняння
28	1	Тригонометричні рівняння
29	1	Лінійні нерівності
30	1	Квадратні нерівності
31	1	Раціональні нерівності
32	1	Ірраціональні нерівності
33	1	Показникові нерівності
34	1	Логарифмічні нерівності
35	1	Тригонометричні нерівності
36	1	Лінійні системи
37	1	Квадратні системи
38	1	Раціональні системи
39	1	Ірраціональні системи
40	1	Показникові системи
41	1	Логарифмічні системи
42	1	Тригонометричні системи
43-45	3	Застосування рівнянь, нерівностей та їх систем до розв’язування текстових задач
	13	Розділ 3. Функції
46	1	Лінійні функції, їх основні властивості
47	1	Квадратичні функції, їх основні властивості
48	1	Квадратичні функції, їх основні властивості
49	1	Степеневі функції, їх основні властивості
50	1	Показникові функції, їх основні властивості
51	1	Логарифмічні функції, їх основні властивості
52	1	Тригонометричні функції, їх основні властивості
53	1	Похідна функції, її геометричний та фізичний зміст
54	1	Похідні елементарних функцій. Правила диференціювання
55	1	Похідна складеної функції, правило її знаходження
56-58	3	Дослідження функції за допомогою похідної. Побудова графіків функцій
	5	Розділ 4. Числові послідовності
59	1	Арифметична прогресія, формула n-го члена
60	1	Сума n перших членів арифметичної прогресії
61	1	Геометрична прогресія, формула n-го члена
62	1	Сума n перших членів геометричної прогресії
63	1	Сума нескінченної геометричної прогресії зі знаменником |q|<1
		Розділ 5. Первісна та визначений інтеграл
64	1	Означення первісної функції
65	1	Означення визначеного інтеграла, криволінійної трапеції
66	1	Таблиця первісних функцій
67	1	Правила знаходження первісних
68	1	Формула Ньютона-Лейбніца
69-71	3	Застосування визначеного інтеграла до обчислення площ криволінійних трапецій

 

Розділ 3. Функції (13год.)

Урок №1

Тема: «Лінійні функції, їх основні властивості».

I. Частина містить завдання та вправи в основному репродуктивного характеру на 1-2 логічних кроки і представлені у формі тестів з вибором однієї правильної відповіді .Для їх розв’зання учням достатньо знати правила, означення ,формули та ознаки , передбачені навчальними програмами.

Запропоновані завдання відповідають I-II рівням навчальних досягнень учнів.

1.Знайти значення функції в точці Х0 :

а) y= - , X0= -0,2.

A)-5;  Б)0,5; В)5; Г)9.

б) у=-,Х0=-0,2.

А)-1; Б); В)1; Г).

в) f(x)=x+3,Х0=-16.

А)7; Б)-1; В)-1; Г)5.

г) f(x)=x+6,X0=14.

A)8; Б)-1; В)13; Г)4.

2.При яких х визначена дана функція:

а) y=.

A(-∞;4) (4;+∞); Б)(-∞;-4);

В(-∞;-4)(4;+∞); Г)(-4;+∞).

б) у=.

А (-∞;-4)(-5;+ ∞); Б) (- ∞;5)(5;+ ∞)

В (-5;+ ∞); Г(-∞;-5)

в) у=

А(-∞;-3)(-3;+ ∞) Б)(- ∞;5)(3;+ ∞);

В(3;+ ∞); Г(-∞;-3).

г) у=

А(-∞;-7)(-7;+ ∞); Б(-∞;7)(7;+ ∞);

В)(-7;+ ∞); Г)(- ∞;7).

3.Яка з функцій є лінійною.

а) А)у=; Б)у=; В)у=+1; Г)у=5

б) А)у=-3х+1; Б)у=; В)у=; Г)у=.

4.Через яку з даних точок проходить графік функції.

а)у=3х-1

А)(2;7); Б)(2;5); В)(-2;5); Г(-2;-5)

б) у=2х+1.

А (2;3); Б)(-2;6); В)(-2;-3); Г)(2;6).

5.Яка з поданих функцій є зростаючою на всій своїй області визначення:

а) А)у=5х; Б)у=-5х; Г)у=5.

Б) А)у=7-х; Б)у=-7х; В)у=-7+х; Г)у=-7-х.

6.Яка з поданих функцій є спадною на всій своїй області визначення:

а) А)у=х+3; Б)у=3х; В)у=; Г)у=-3х.

б) А)у=0,3х-5; Б)у=5-х; В)у=5; Г)у=х.

7.Графік якої з наведених функцій проходить через початок координат:

а) А)у=; Б)у=5х; В)у=5-х; Г)=5+х.

б) А)у=; Б)у=; В)у=4-х; Г)у=4+х.

8.При якому значенні х невизначена функція:

а)у=.

А)-4; Б)-2; В)-2;4; Г)2.

б)у=.

А)4; Б)1;4; В)-1;-4; Г)-4.

9.Знайдіть точку перетину графіка функції з віссю Оу:

а)у=-3х-7.

А)(-3;-7); Б)(0;-7); В)(-;0); Г)(0;-).

б)у=4х-5.

А)(-5;4); Б)(0;15); В)(5;0); Г)(0;5).

10.Знайдіть точку перетину графіка функції з віссю Ох:

а)у=-3х+15

А)(15;0); Б)(0;15); В)(5;0); Г)(0;5).

б)=-12+6х.

А)(0;2); Б)(2;0); В)(12;0); Г)(-12;0).

11.Яка з функцій є оберненою пропорційністю:

а) А)у=2х; Б)у=2х-3; В)у=; Г)у=

б) А)у=-5х; Б)у=-; В)у=2х-2; Г)у=.

12.Яка з поданих прямих перетинає задану пряму:

а)у=2х+3?

А)у=х+5; Б)у=2х-3; В)у=2х-2; Г)у=2х+5

б)у=-3х+7?

А)у=3х+5; Б)у=-3х+4; В)у=-3х; Г)у=-3х-5

13.Графік якої функції зображено на малюнку:

а)                 у                         А)у=х-3;

                                               Б)у=х+3;

                                 3       х   В)у=-х+3;

                                                Г)у=-х-3

                         -3

 

б)                    у                            А)у=х+2;

                                                      Б)у=2х;                  

                         2                           В)у=х;

                               1                х   Г)у=-2х

 

 

II частина – це завдання III рівня навчальних досягнень учнів . Учень самостійно застосовує знання в стандартних ситуаціях,уміє виконувати математичні операції загальна методика і послідовність яких йому знайомі , але зміст та умови виконання змінені.

14.Побудуйте графік функції у=0,5х-3.Чи належить цьому графіку точка А(-18;-12)?Користуючись графіком знайдіть проміжки знакосталості.

15.Побудуйте графік функції у=1,5х+4. чи належить цьому графіку точка А(-18;23)? Користуючись графіком,знайдіть проміжки знакосталості.

16.Побудуйте графік функції у=2х-5 знайдіть за графіком:

А) значення у, при якому х=-1;1;4;5

б) значення х, якщо у=-1,6;

в) значення х, при яких у>0,y<0.

18. Функція задана формулою у=:

а) знайдіть значення функції,якщо х=-1;0;11;

б) при якому значенні х значення функції дорівнює 8;-2;5.

19.Функція задана формулою у=.

а) знайдіть значення функції,якщо х=-3,5∙х=1;х=13;

б)при якому значенні х значення функції дорівнює 20;0.

20. Побудуйте графіки функцій та знайдіть координати точок перетину графіків:

а) у=2х+4 і у=-2х;

б) у=-2х+4 і у=2х.

21.Побудуйте графік функції у=2х-1.Чи проходить графік функції через точку А(-25;-57)?

22.Побудуйте графік функції у=-2х+3 чи проходить графік функції через точку В(20;-37)?

23.Побудуйте графік функції

а) у=-х+1,5; б) у=х-2,5.

Вкажіть координати точок перетину графіка з осями координат.

III частина містить завдання IV рівня навчальних досягнень учнів та завдання поглибленого рівня  це задачі та вправи,розв’язання яких вимагає вміння орієнтуватися в нестандартних ситуаціях,застосовувати оригінальні строгості суджень.

24.Побудуйте графік функції.

а)

б) у=

в) у=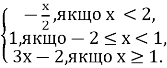

г) у=

25. Графік лінійної функції проходить через точки А і B. Задайте цю функцію формулою, якщо

а) А(0;2), В (3;-1); б) А(2;-5), В(0;1); в) А(-5; 32), В(3;-8); г) А(4;-5), В(-2; 18).

 

 

Урок №2 , №3
Тема: «Квадратичні функції, їх основні властивості»
| частина
Яка з функцій є квадратичною ?

1. А) y= 3x-4;                         Б) y= x+3;                        В) y=                                     Г)y=x²+3x-4;
2. A) y= ;                              Б) y=;                В) y=x²-9x+8;                                     Г)y= -x – 9;
3.Знайдіть значення функції  y=x² - 3x в точці x₀  = 2
    А)2;                                     Б)-2;                                 В)-4;                                                    Г)10;
4.Знайдіть значення функції  y=x² + 3x в точці x₀ = 2
    А)14;                                    Б)7;                                 В)10;                                                    Г)8;
5.Функція задана формулою f(x)=x² + 4x. Знайдіть f(-2).
    А)12;                                     Б)4;                                 В)-12;                                                   Г)-4;

6.Функція задана формулою f(x)= x²- 3x. Знайдіть f(1).

    А)-2;                                      Б)2;                                 В)-4;                                                     Г)4;

7.y=x²-3x-10;

    А)А(5;0);                               Б)В(-5;0);                       В)С(3;10);                                           Г)D(-3;10);

8.y=x²-x-12;

    А)А(3;0);                               Б)С(-3;0);                       В)D(4;2);                                             Г)В(0;12);

9.y=x²+1;

   А)А(-4;17);                            Б)К(-2;-3);                     В)Н(4;16);                                           Г)N(-4;-15);

10.y=-2x²+3;  

  А)F(2;5);                                Б)N(-1;5);                       В)A(-2;5);                                           Г)K(-1;1);

11.y=x²+a проходить через точку В(1;-1)?

  А)a=-3;                                  Б) a= 2;                           В) a= 3;                                               Г)a=-2; 

12.y=ax² проходить через точку D(2;-8)?

  А) a= 2;                                 Б)a=-2;                            В) a= 4;                                               Г)a=-4;

13.y=x²+2, В(-1;y).

  А)3;                                       Б)-1;                                 В)1;                                                     Г)-3;

14.y=1-x²,А)(x;-24)

  А)-5;5;                                  Б)5;                                  В)-5;                                                    Г)-;.

                                                                                                                                                                            15. y=-x²-6x-5;

  А) [4;+);                            Б)(-;4];                       В) (-;4);                                         Г) (4;+);

16.y=2(x-3)²+6;

  А)9;                                       Б)6;                                В)4;                                                   Г)10;

17. y=-2(x-3)²+6;

   А)7;                                      Б)-2;                               В)3;                                                  Г)-10;

18.y=;

   А)x(-;2)(2;3)(3;+);                                     Б)x(-;0)(0;+);

   В)x(-;-3)(-3;-2)(-2;+);                                Г)x(-;2)(3;+);

19.y=;

   А)x(-;0)(0;+);                                                 Б)x(-;-1)(1;+);

   В)x          Г)x       

20.y=3x²-24x+21;

    А)21;                                    Б)-1;-7;                          В)1;7;                             Г)функція нулів не має.

21.y=5x²+10x-15;

   А)-15;                                   Б)-1;3;                            В)1;-3;                           Г)функція нулів не має.

22.y=x²-10x-24;

   А)12;-2;                               Б)6;-4;                            В)-12;2;                         Г)-6;4;

23.y=x²-6x-40;

  А)-10;4;                                Б)-5;8;                            В)10;-4;                         Г)5;-8;

24. y=x²+5x+3;

  А)1;                                       Б)5;                                В)3;                                 Г)9;

25.y=x²-6x-7;

  А)-7;                                     Б)-6;                               В)1;                                 Г)-13;

26.y=x²-8x+12;

  А) (-4;-4);                            Б) (4;4);                         В) (4;-4);                         Г) (-4;4);

27.На осі ординат;

  А)y=-x²+3x;                      Б)y=-x²+3x+4;                В)y=-x²+3;                        Г) y=-(x-3)²+3;

28.На осі абсцис;

  А)y=x²+6x;                      Б)y=x²+6x+9;                  В) y=x²+6;                         Г)y=x²+6x-7;

29.y=x²+2x-3;

  А)y=-1;                           Б)y=-5;                             В)y=-4;                              Г)y=7;

30.y=-x²+2;

 А)y=-2;                            Б)y=2;                              В)y=1;                               Г)y=-1;

II частина

31.Побудуйте графік функції і знайдіть проміжки знакосталості y=x²-5x+6.

32.Побудуйте графік функції y=x²-2x-3. Знайдіть проміжок на якому функція зростає.

33.Побудуйте графік функції y=x²-2x-3. Знайдіть проміжок на якому y0.

34.Побудуйте графік функції y=x²+4x-5. Знайдіть проміжок на якому y0.

35.Побудуйте графік функції y=-x²+6x-5. Знайдіть найбільше значення функції.

36.Побудуйте графік функції y=x²-6x+5. Знайдіть найменше значення функції.

37.Побудуйте графік функції y=-x²+1.При яких значеннях х, функція приймає додатні значення?

38.Побудуйте графік функції y=-x²+1.При яких значеннях х, функція приймає додатні значення?

39.Побудуйте графік функції y=x²-2х+3 на проміжку [0;3]. Користуючись графіком знайдіть область значення функції.

40.При яких значеннях х невизначена функція y=?

41.Чому дорівнюють абсциси точок перетину даної параболи с віссю ОХ  y=x²-5х-24?

42.Знайдіть ординату точки перетину графіка функції з віссю ординат  y= x²+8x-1.

43.Які абсциси мають точки перетину графіків функції  y=3х-x² і y= x²-х.

44.Знайдіть координати точок перетину прямої і параболи 2х-у+2=0 і у=2x²+5х-7.

45.Графіку функції у=2x²+bx+3 належить точка А(-1;6). Знайдіть b.

46. Графіку функції у=-x²-3x+с  належить точка А(-2;5). Знайдіть с.

47. Графіку функції у=ax²+4x-3 належить точка А(1;2). Знайдіть a.

48.Побудувати графік функції у=x²-4х+3.

      За графіком визначити:

      А)значення у, якщо х=2;

      Б)значення х, якщо у=3;

      В)нулі функції.

III частина

49.Побудувати графік функції і за графіком визначити область значення функції,

      проміжки знакосталості, спадання і зростання у=.

50.Знайдіть допустимі значення змінної х функції  у=;

51.Знайдіть допустимі значення змінної х функції  у=;

52.Знайдіть область визначення функції у=+;

53.Побудуйте графік квадратної функції у= x²-4х+а,якщо її найменше значення дорівнює 1.

54.Знайти проміжок спадання функції:у=(х-6)(х+2);

55.Знайти точки параболи, у яких абсциси та ординати однакові:у=x²-6х+10;

56.Знайти точки графіка функції,у яких абсциса та ордината є протилежними числами:

      у=x²+2х-10;

57.Знайти значення с,при яких функція набуває тільки від’ємних значень:

     у=-x²-6х-с;

58.Знайти значення с,при яких усі точки графіка функції лежать вище від осі х:

      у=x²-10х+с;

59.Побудуйте графік даної функції f(x). За графіком визначити область значень функції,проміжки знакосталості,зростання і спадання: f(x)=-2x²-8x-6;

60.Графік квадратної функції з вершиною А(1;1) проходить через точку С(-1;5). Знайти коефіцієнт а,b і c у формулі функції.

61.Графік квадратичної функції належать точки А (3;-3), В (2; 3)і С (7;13). Записати формулу цієї функції.

Урок №4
Тема: «Степеневі функції, їх основні властивості»
| частина
 

1.Скільки коренів має рівняння?

             а ) х⁴+1=0;                                                                                б ) х³+1=0;

А) Жодного;             Б) тільки один;              В) два;                Г)безліч;                Д) визначити неможливо;

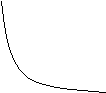
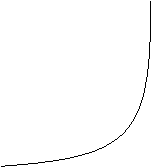
2.Установіть відповідність між функціями, заданими формулами (1-4)та їхніми графіками(А-Д).

а ) 1) y= ;                                                                               б ) 1) y=

     2) y=x^-2;                                                                                     2) y=x^-3;

     3) y=                                                                                     3) y=;

     4) y= ;                                                                                  4) y=;

 

А)                       у                                              Б)                       у

 

      

В)                          у                                                        Г)                           у

 

 

 

                                 0                                                 х                                           0                                                  х

 

 

 

Д)                                   у

                                                                                

 

 

 

 

0.                                                                                        х

 

3.Знайдіть область визначення функції:

    а ) у=;                                                б ) у=;

А) (-           Б) (-];            В) (1;+);           Г) [1;+);            Д) R;

4.Установіть відповідність між функціями, заданими формулами (1-4), та їхніми областями визначення:

     1) у=х^-6;                                     

     2) у=;

     3) у=;

     4) у=;

    А) (-          Б) [0;+);       В) (0;+);

    Г) (-;+);         Д) (-(0;+);

5.Зобразити схематично графіки функцій, записати їх область визначення та область значення:

    а ) f(x)=;                  б )  g(x)=;                   в )  u(x)=. 

6.Що більше:

   а )   або ;                             б )   або ;

7.Що менше:

   а )  або ;                              б )   або ;

8.Порівняйте числа:

   а ) і ;                             б ) і ;                        в ) і ;

9.Порівняти числа:

   а ) і 0;              б ) і 1;              в ) і ;                г ) і ;

10.При яких Х має зміст вираз:

      а ) ;           б);                в ) ;                   г);

11.Знайдіть область визначення функції:

      а ) у=х⁷;         б ) у=х^-3;           в ) у=;          г ) у=;       д ) у= ;

12.Побудуйте графік функції:

      а ) у=х⁴;                                   б ) у=х⁷.

II частина

13.Знайдіть область значень функції  f(x)=3-.

14.Порівняти числа:

      а ) і ;                      б ) і .

15.Порівняти числа:

      а ) і ;                      б ) і 5^0,4;

16.Порівняти числа:

     а ) і ;                              б ) і ;

17.Розв’яжіть рівняння:

     а ) х³=7;            б ) х⁸=3;           в ) х⁵=-5;           г ) х⁸=-13;             д ) х⁴=16;

18.Побудуйте графік функції :

    а ) у=х^-3;            б ) у=х^-4;          в ) у=;            г ) у=;

19.Знайдіть область визначення функції:

    а ) у=;                              б ) у=;

III частина

20.Побудуйте і порівняйте графіки функцій:

  а ) у= і у=;                          б ) у= і у=.

21.Побудуйте графік функції:

 а ) у=(х+1)⁴;                б ) у=-3;                 в ) у=;                 г ) у=;

22.Розв’яжіть  графічно рівняння:

 а ) =6-х;                  б ) =х²;                  в ) =2-х;                г ) =2х-1;

23.Знайдіть область визначення функції:

 а ) у=;                                   б ) у=;

24.Знайдіть область визначення функції:

 а ) у=;

 б ) у=.

 

 

 

25.Побудуйте графік функції:

      У=якщо х

26.Знайдіть проміжки знакосталості функції:

     а ) у=;                  б ) у=.

Урок № 5.

Показникові функції, їх основні властивості

1.          частина

1.Якщо графік функції y проходить через точку M(2;4 ), то а дорівнює:

А); Б) 1; В) 2;Г) -2; Д) 4

2.Порівняти m та n,якщо (^m˃()ⁿ

А)m˃n;Б ) m≥n;В) m˂n;Г) m≤n;Д)m=n

3. Порівняти числа та 1

А)2,5^-√2˂1;Б)2,5^-√2˃1;В) 2,5^-√2 =1

4. Областю визначення функції y= ()^xє проміжок:

А) (-;0);Б) (0;);В) (-;); Г) [0;)

5. Яка з функцій зростає:

А) y=0,018^x;Б) y=()^x; В) y=7^x; Г) y=^x

6. Яка с функцій спадає

А) y=2^x;Б)y=()^x; В) y=()^x; Г)y=