11 клас. Конспект уроку № 4

Тема:«Розв’язування показникових рівнянь»

 Мета : формування умінь та навичок розв’язувати показникові рівняння способом зведення до спільної основи; способом винесення за дужки спільного множника; способом зведення до спільного показника; графічним способом.

Тип уроку:формування умінь та навичок.

 

Хід уроку

І. Перевірка домашнього завдання.

          Поки клас усно перевіряє домашнє завдання, два учня біля дошки розв’язують №174 стор.208 (Шкіль)

І учень із А № 1; 3; 8:

1) 2^𝑥 = 64

2^𝑥 = 2⁶

𝑥 = 6

3) 2^−𝑥 = 16

2−𝑥 = 24

−𝑥 = 4

𝑥 = −4

8) 𝑎𝑥²−7𝑥+12 = 1𝑎𝑥²−7𝑥+12 = 𝑎0

𝑥² − 7𝑥 + 12 = 0

𝑥 = 3;        𝑥 = 4

II учень із А № 2; 5; 9:

2) 2^2𝑥 = 512

22𝑥 = 29

2𝑥 = 9

𝑥 = 4,55)32𝑥−1 = 81

32𝑥−1 = 34 2𝑥 − 1 = 4

2𝑥 = 5

𝑥 = 2,5

9) 𝑎(𝑥−1)(𝑥+2) = 1

𝑎(𝑥−1)(𝑥+2) = 𝑎0

(𝑥 − 1)(𝑥 + 2) = 0

𝑥 − 1 = 0;     𝑥 + 2 = 0𝑥 = 1;           𝑥 = −2

 

II. Набуття умінь розв’язувати показникові рівняння

          Ви вже вмієте розв’язувати найпростіші показникові рівняння.

 А зараз розглянемо І спосіб: приведення рівняння до спільної основи, тобто до рівняння виду 𝑎^𝑓(𝑥) = 𝑎^𝐺(𝑥).

Шкіль №174(10;11;23) стор.208

10)                       2^𝑥 ∗ 5^𝑥 = 0.01

(2  ∗ 5)^𝑥 = 0.1²

10^𝑥 = 0.1²

10^𝑥 = 10⁻²

𝑥 = −2

 

11)                       2^𝑥 ∗ 5^𝑥 = 0.1 ∗ (10^𝑥−1)⁵

(2  ∗ 5)𝑥 = 10−1 ∗ 105𝑥−5

10𝑥 = 105𝑥−6

𝑥 = 5𝑥 − 6

𝑥 − 5𝑥 = −6 −4𝑥 = −6

𝑥  

𝑥  

𝑥 = 1.5

 

        23)           

 

 

 

 

 

(²)2𝑥−3𝑥+3 = (²)1

                   3                         3

 

2𝑥 − 3𝑥 + 3 = 1

−𝑥 + 3 = 1

−𝑥 = 1 − 3

−𝑥 = −2

𝑥 = 2

Розглянемо II спосіб: винесення спільного множника за дужки.

Шкіль №174(13;12) стор.208

        13)          7^𝑥 − 7^𝑥−1 = 6

7^𝑥−1 ∗ (7 − 1) = 6

7^𝑥−1 ∗ 6 = 6

7𝑥−1 = 1

7𝑥−1 = 70

𝑥 − 1 = 0

𝑥 = 1

 

        12)           2^𝑥+2 − 2^𝑥 = 96

2^𝑥 ∗ (2² − 1) = 96

2^𝑥 ∗ (4 − 1) = 96

2^𝑥 ∗ 3 = 96

2^𝑥 = 96/3

2^𝑥 = 32

2^𝑥 = 2⁵

𝑥 = 5

 

3) 52𝑥−1 − 52𝑥 + 22𝑥 + 22𝑥+2 = 0

52𝑥

 

 

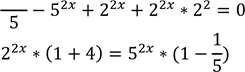
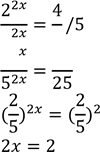                5           5

                2²             4

 

𝑥 = 1

Розглянемо IIІ спосіб: приведення рівняння до квадратного.

49^𝑥 − 8 ∗ 7^𝑥 + 7 = 0

7^2𝑥 − 8 ∗ 7^𝑥 + 7 = 0

Введемо нову змінну 7^𝑥 = 𝑡

𝑡² − 8𝑡 + 7 = 0

𝑡₁ = 7;         𝑡₂ = 1

Повернемось до минулої змінної

7^𝑥 = 7;         7^𝑥 = 1

7^𝑥 = 7¹;        7^𝑥 = 7⁰

𝑥 = 1;          𝑥 = 0

 

Розглянемо графічний спосіб розв’язування рівнянь. 1. Розв’язати графічно рівняння (^𝟏)^𝒙 = 𝒙 + 𝟏. 

𝟑

В одній і тій самій системі координат будуємо графіки функцій

 

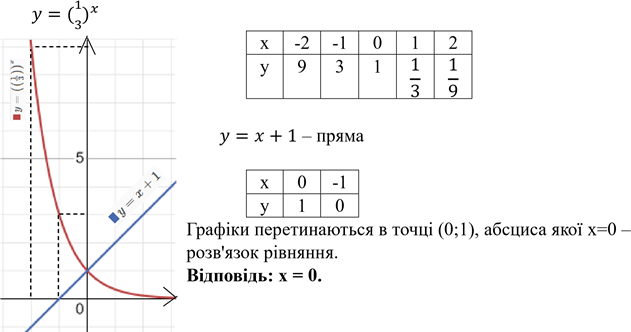
2. Розв’язати графічно рівняння 𝟑^𝒙 = 𝟒 − 𝒙

В одній і тій самій системі координат будуємо графік функцій

𝑦 = 3^𝑥

x	-2	-1	0	1	2
y			1	3	9

 

𝑦 = 4 − 𝑥– пряма

x	0	4
y	4	0

Графіки перетинаються в точці (1; 3), абсциса якої x=1 – розв'язок рівняння.

Відповідь: x=1  

ІІІ. Підсумок уроку.

ІV. Домашнє завдання: збірник, стор.78 №189 (1-7);  №190 (1); 191(1).