Розробка уроку геометрії у 7 класі «Вертикальні кути та їх властивості»

Розробка уроку геометрії у 7 класі

«Вертикальні кути та їх властивості»

Мета:

навчальна: сформувати поняття вертикальних кутів; домогтися засвоєння теореми про рівність вертикальних кутів; сформувати вміння застосовувати ці знання до розв’язування задач;

розвивальна: сприяти розвитку уваги, пізнавальних здібностей учнів; формувати вміння аналізувати, виділяти головне в інформації;

виховна: виховувати старанність, відповідальність, творче ставлення до справи

Тип уроку: засвоєння знань, умінь та навичок

Вид уроку: урок – казка

Обладнання:  підручник, картки із завданнями

Хід уроку

І. Організаційний етап

Учитель. Сашко повертався зі школи і розповідав своїм друзям, які пригоди з ним трапляються і як вони допомагають йому у навчанні. Повідомив їм також про те, що знову чекає чергової казкової подорожі. І тільки він промовив ці слова, зразу відчув знайомий дотик і вмить опинився перед брамою Кутинська. На брамі, як завжди, були вивішені завдання, які необхідно виконати, щоб потрапити до міста. Оскільки на цей раз, завдання були практичного змісту, то Сашко приступив до їх виконання. Пропоную і вам виконати ці завдання.

ІІ. Перевірка домашнього завдання, актуалізація опорних знань

1. Перевірка завдання, заданого за підручником

Учитель. Об’єднаємося у дві команди. Одна команда задає запитання іншій по темі «Суміжні кути та їх властивості». Потім міняємося ролями. (Запитання та відповіді учнів)

2. Математичний диктант

ІІІ. Актуалізація опорних знань

Виконання усних вправ

1) Знайдіть величину кута, суміжного з кутом 40° , 90° , 150°.

2) Величина одного з кутів, суміжного з даним кутом, дорівнює 70°. Чому дорівнює величина іншого кута, суміжного з даним кутом?

3) На наведених рисунках укажіть кути, суміжні з кутом 1.

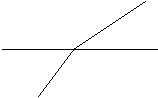
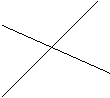а)                                              б)                                            в)

               2           1                              2               

          3       4                                3      4        1                6     1        2                                                

                                                                                         5     4              3       

ІV. Вивчення нового матеріалу

План вивчення теми

1.   Означення вертикальних кутів.
2.   Теорема про рівність вертикальних кутів.

Учитель. Сашко виконав усі завдання, які були перепусткою до казкового міста, а тому брама перед ним відчинилася і він, на своє здивування,  побачив зовсім нове місто. Кудись поділася вулиця, яка нагадувала розгорнутий кут, а перед Сашком з’явилися красиві котеджі. Їх було багато. Хлопець пройшовся вулицею і біля одного з котеджів зустрів знайомих кутів: Гострого, Прямого, Розгорнутого і Тупого.

•       А що сталося? – поспішив запитати Сашко. Місто якось змінилося, -продовжив він.
•       Не хвилюйся, ти потрапив до того самого міста Кутинська, що й був раніше, - заспокоїв його Тупий кут.
•       Просто, у міста є така особливість, що воно відкриває перед відвідувачами ту свою сторінку, яка їм ще невідома, - пояснив Прямий кут.
•       Сьогодні ти познайомишся з новими кутами, які живуть цілими родинами: деякі кути ти уже знаєш, а деякі тобі ще незнайомі, - повідомив хлопцеві Розгорнутий кут.

Учитель. Оскільки, ви також впоралися із поставленими завданнями, то я вам пропоную подорожувати разом із Сашком. Згода? Отож, вперед за новими знаннями!

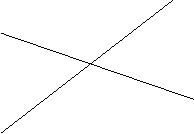 А Сашко разом із своїми знайомими кутами уже прямував до одного з котеджів. Прямий кут подзвонив у двері, які зразу відчинилися, і хлопець побачив аж чотири кути разом, які не могли існувати один без одного, тому що мали одну вершину і спільні сторони. Виглядали вони так:

                                                                   2      3

                                                       1          4

Розгорнутий кут пояснив мешканцям котеджу, що Сашко навчається у сьомому класі і дуже хоче дізнатися про кути все. А тому сьогодні настала черга поспілкуватися з ними.

•       Я хочу, щоб ви мені розповіли про себе, - сказав Сашко загадковим кутам.
•       А давай ти сам, дивлячись на нас будеш про нас говорити все, що ти знаєш. Адже, деякі кути тобі відомі, - запропонували кути.
•       Згода, - відповів Сашко – але якщо я щось скажу не так, то ви мене поправите.

Учитель. І хлопець, дивлячись на кути, розповідав про них, робив свої припущення і висновки. Давайте і ви спробуєте самостійно охарактеризувати кути і з’сувати їх назву. (Відповіді учнів)

Учитель. Отже, Сашко і ми з вами з’ясували, що кути 1 і 2, 2 і 3, 3 і 4, 4 і 1 – це суміжні кути. А кути 1 і 3, 2 і 4 – це вертикальні кути. Вони запропонували Сашку самому, дивлячись на них і користуючись своїми знаннями, зрозуміти, яку властивість вони мають. І я вам також це пропоную (доведення властивості вертикальних кутів учнями без користування підручником)

Учитель. Сашко був задоволений, що він впорався із завданням без допомоги. А я також задоволена, що ви самостійно здобули нові знання. Але послухаємо,  про що говорили кути і Сашко.

- Цікаво, - сказав Сашко, - суміжні кути в сумі дорівнюють 180° , а вертикальні кути – рівні.

•       Так, серед суміжних кутів старшим братом є той кут, у якого більша градусна міра, - сказав один із кутів.

-  Оскільки вертикальні кути – рівні, то вони є братами-близнюками, - продовжив інший кут.

•       Знання, які ти отримав сьогодні значно допоможуть тобі при розв’язуванні задач, навіть, у старших класах, - сказали хором кути.

Учитель. Ми також будемо зараз розв’язувати задачі для закріплення, отриманих знань

Фізкультхвилинка

«Естафета з варіаціями»

Написати слово або коротеньку фразу (кожному по одній букві) - який ряд швидше. При цьому дотримуватися  порядку - перший учень сів на місце, тільки тоді встав другий.

V. Засвоєння нових знань і вмінь

1. Робота з підручником

Усно: № 105, 106, 107

Письмово: № 109, 110, 117, 121, 122

2.     Додаткові завдання

1) За перетину двох прямих утворилося чотири кути. Знайдіть ці кути, якщо відомо, що градусні міри двох із них відносяться як 4 : 5.

2) За перетину двох прямих утворилося чотири кути. Знайдіть ці кути, якщо відомо, що один із них на 60  більший, ніж половина другого.

3) За перетину трьох прямих, які проходять через одну точку, утворилося 6 кутів. Доведіть, що сума кожних із трьох цих кутів, не прилеглих один до одного, дорівнює двом прямим кутам.

VІ. Підсумки уроку

Учитель. Ми сьогодні знову мандрували казковим містом Кутинськом і отримували нові знання. Отож, давайте підсумуємо їх. Я зачитую вірш, а ви  кажете назву кутів, які ми сьогодні розглядали.

Ці кути оригінальні,

Їхні сторони – промені доповняльні.

А вершина в них одна

Й рівна їх величина.

Тож, давайте пригадаєм,

Як ми їх називаєм.  (ВЕРТИКАЛЬНІ КУТИ)

Учитель. У вірші про кути згадується їх властивість. Сформулюйте її. (Відповіді учнів)

Рефлексія

Візьміть чистий аркуш паперу і складіть із нього літачок. На крилах літачка напишіть свої враження про урок.

VІІ. Домашнє завдання

1. Завдання за підручником  § 6,   № 118, 123