Розробка уроку "Кут між площинами"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Геометрія. 10- 11 класи.

 

Урок повторення.

 

 

 

 

 

 

 

 

Наталія Броніславівна Каштан - викладач математики

ДПТНЗ "Рівненський центр професійної технічної освіти сервісу та дизайну"

 

 

 

Тема: Кут між площинами

Мета:

Навчальна:

Систематизувати та узагальнити знання і вміння учнів по застосуванню методів: побудови лінійного кута двогранного кута і паралельних площин для вирішення завдань на знаходження кута між площинами.

Створити умови для відпрацювання учнями навичок, необхідних при вирішенні задач на знаходження кутів між площинами обчислювальними методами.

Розвиваюча:

Розвивати  у учнів творче самостійне мислення та інтелектуальні якості: здатність до «бачення» проблеми.

Розвивати вміння науково аргументувати, чітко і ясно викладати свої думки, підходити до вирішення завдань з дослідницької позиції.

Виховна:

Створити умови для становлення суб'єктної позиції учнів при підготовці до підсумкової атестації, підвищення їх мотивації.

Виховувати самостійність, акуратність і сумлінність при виконанні заданій.

Виховання волі і наполегливості в досягнення поставленої мети; завзятості і інтересу до вирішення завдання з позиції дослідника.

 

План уроку.

I. Організаційний момент.

II. Повторення: 1). Визначення двогранного кута.

                            2). Вимірювання двогранного кута.

                             3). Визначення кута між площинами.

                             4). Теорема про три перпендикуляри.

III. Завдання на готових кресленнях

IV. Розв'язання завдань на знаходження кута між площинами.

V. Демонстрація рішення задачі на знаходження кута між площинами рівня С.

VI. Підсумки уроку.

VII. Завдання до дому (3- рівневі).

 

 

 

 

Хід уроку.

I. Організаційний момент.

II. Повторення:

1). Визначення двогранного кута.

У геометрії двогранний, діедральний або торсійний кут — геометрична фігура, утворена двома півплощинами, обмеженими спільною прямою. Півплощини, які утворюють фігуру такого кута, називають гранями, а пряму, що їх обмежує, ребром. Для визначення його величини використовується кут, утворений двома напівпрямими, що виникають внаслідок перетину двох напівплощин третьою перпендикулярною до їх ребра площиною і називається лінійним кутом двогранного кута.

 

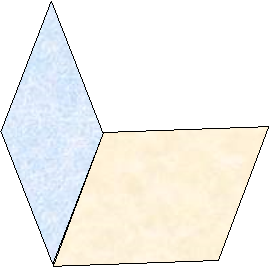
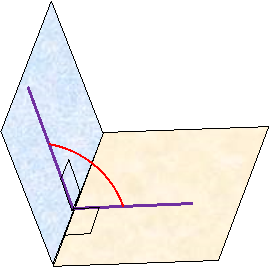
2). Вимірювання двогранного кута. Двогранний кут вимірюється лінійним кутом.

АОВ – лінійний кут двогранного кута ACDB.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0º<<180º.

 

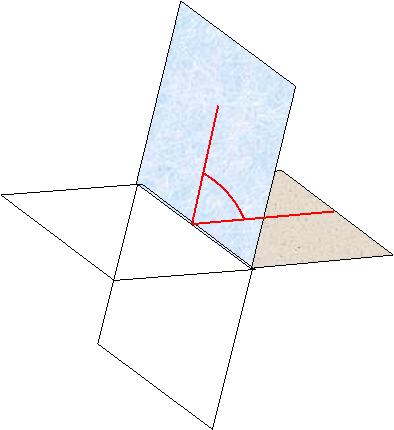
3). Визначення кута між площинами.

Дві пересічні площині  утворюють дві пари рівних  двогранних кута. Один з них кут є кутом між площинами 0º<<90º.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

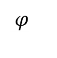
4) Теорема про три перпендикуляри.

 Якщо пряма, проведена на площині через основу похилої, перпендикулярна її проекції, то вона перпендикулярна й самій похилій. 

 

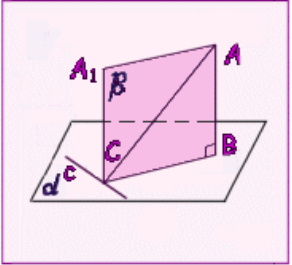
Якщо пряма на площині перпендикулярна похилій, то вона перпендикулярна і проекції похилої.

III. Завдання на готових кресленнях

Знайти кут між площинами α і β

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

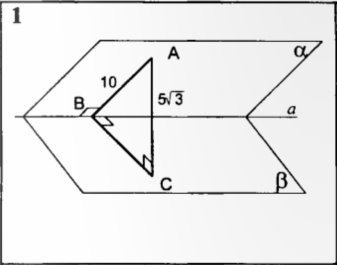
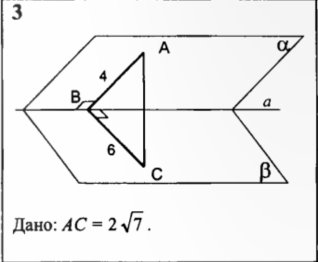
IV. Розв'язок задач

Задача 1. Сторона основи правильної трикутної призми АВСА₁В₁С1 дорівнює 2, а діагональ бокової грані дорівнює. Найти кут між площиною А₁ВС і площиною основи призми.

Розв'язок

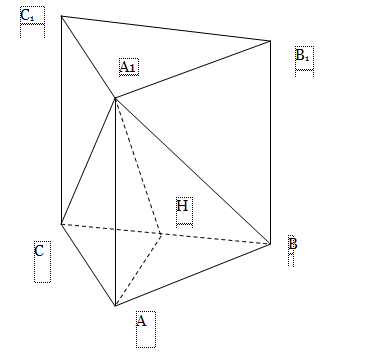
Позначимо Н як середину ребра ВС. Так як АВС рівносторонній, а А₁ВС – рівнобедрений, відрізки АН и А₁Н перпендикулярні ВС. Таким чином, А₁НА – лінійний кут двогранного кута с гранями ВСА і ВСА₁.  З АА₁В найдемо  АА₁=1.  З АНВ найдемо АН=. ЗНАА₁  найдемо tgА₁НА=. Тоді шукаємий кут рівний 30◦.

Відповідь: 30◦.

Задача 2. Основа піраміди МАВСD – прямокутник АВСD зі сторонами 3 и 4. Ребро МА перпендикулярно площині АВD, а кут між площинами МВD и АВD дорінює 45◦. Знайти об'єм піраміди.

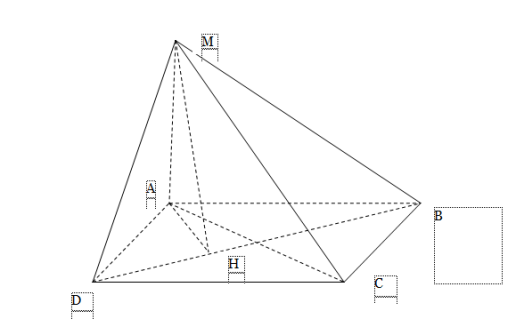
Розв'язок. Проведемо в площині основи перпендикуляр АH до прямої ВD. Тоді АН – проекція  похилої НМ на площину основи. По ТТП МН ВD и АНМ – лінійний кут двогранного кута АВDМ. За умовоюАНМ=45◦, о це означає, АН=АМ. З прямокутника АВD найдемо висоту АН, проведену до гіпотенузи: АН=.

Це означає, висота піраміди АМ=, и обєм піраміди дорівнює ∙3∙4∙=9,6.

Відповідь: 9,6

V. Демонстрація рішення задачі на знаходження кута між площинами рівня С

VI. Підсумки уроку.

VII. Домашнє завдання (3-рівні).

Рівень А

Ребро  CD тетраедра ABCD перпендикулярна площині АВС, АВ = ВС =АС =6, BD = 3. Найти двогранний кут DACВ.

Рівень В

Найти кут φ між площинами трикутника АВС і прямокутника АВМN, якщо АВ = 5 дм, ВС = 12 дм, АС = 13 дм, ВМ = 15 дм, МС = 9дм.

Рівень С

Основа піраміди DABC- рівнобедренний трикутник АВС, в якому АВ = ВС = 13, АС = 24. Ребро DB перпендикулярно площині основи і дорівнює 20. Знайти тангенс двогранного кута при ребре АС.