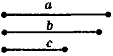Розробка уроку на тему "Геометричні побудови"
Тема. Геометричні побудови
Мета: Засвоєння учнями: поняття «геометрична побудова», розхил циркуля, задання умови задачі в геометричній формі; алгоритму побудови трикутника за даними трьома сторонами; алгоритму побудови кута, що дорівнює даному; алгоритму побудови бісектриси кута і алгоритму ділення відрізка навпіл. Вироблення вмінь відтворювати вивчені алгоритми і виконувати дії, описані в них; відпрацювання навичок володіння креслярськими інструментами (для вимірювання і побудови прямих, відрізків, кіл та дуг кіл) і навичок проведення аргументованих міркувань із посиланням на вивчені означення, властивості і ознаки рівних відрізків, кутів та трикутників (при доведенні правильності здійснених побудов).
Тип уроку: засвоєння знань, вироблення вмінь.
Обладнання: набір демонстраційного креслярського приладдя, таблиця № 22 «Геометричні побудови».
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Методичний коментар
Для перевірки виконання домашнього завдання можна провести самостійну роботу за готовими рисунками, що відтворюють типові ситуації, вивчені на попередньому уроці, або організувати взаємоперевірку робіт учнів за зразком (при недостатньо високому рівні підготовки учнів).
Самостійна робота за готовими рисунками
Знайдіть кут х за даними рисунка:
варіант 1 — рис. 133; варіант 2 — рис. 134.
Варіант 1.
На рис. 133: а) α = 21°; β = 49°; б) α = 12°; β = 64°; в) α = 18°; β = 34°.
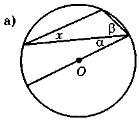
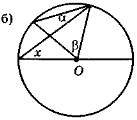
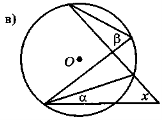
Рис. 133
Варіант 2.
На рис. 134: а) α = 19°; β = 47°; б) α = 18°; β = 46°; в) α = 18°; β = 34°.
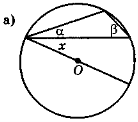
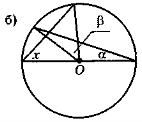
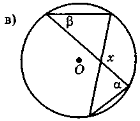
Рис. 134
III. Формулювання мети і завдань уроку
На цьому етапі уроку доречним буде слово вчителя про практичне застосування геометрії в професійній діяльності людини, наприклад для виконання креслень. Отже, цілком логічним буде зосередити увагу учнів на розв'язуванні задач, у яких треба не обчислювати значення невідомих величин із використанням вивчених властивостей фігур (зображення фігур при цьому не відтворюють точних значень довжин відрізків та градусних мір кутів), а відтворювати зображення фігури у точній відповідності із заданими значеннями величин її елементів, причому робити це у певній послідовності і аргументувати цю послідовність, посилаючись на вивчені властивості фігур. Зрозуміло, що вивчення матеріалу, пов'язаного з розв'язанням такого типу задач, буде основною метою поточного і наступних п'яти уроків.
IV. Актуалізація опорних знань і вмінь учнів
Учні вже знають з курсу математики п'ятого класу, як побудувати трикутник за трьома сторонами. Тому, перед вивченням матеріалу уроку, можна апелювати до знань і вмінь учнів, набутих у п'ятому класі, а саме: запропонувати до розв'язання таку задачу.
Задача
Скориставшись означенням трикутника, учень накреслив у зошиті довільний трикутник ABC. Які вимірювання він повинен виконати, щоб накреслити поряд із трикутником ABC інший трикутник МРК, рівний трикутнику ABC? Яким чином він має виконати ці вимірювання, щоб вони були найточнішими? Як скористатися цими вимірами для успішного розв'язання задачі?
Після обговорення можливих варіантів розв'язання окреслюємо коло питань, над вивченням яких працюватимемо і далі.
V. Засвоєння нових знань
План вивчення нового матеріалу
- Що означає «побудувати геометричну фігуру»? Які елементарні побудови можна виконувати за допомогою циркуля та лінійки? Що означає задати умову задачі в геометричному вигляді? Що таке «алгоритм»?
- Алгоритм побудови трикутника за трьома сторонами.
- Алгоритм побудови кута, що дорівнює даному.
- Алгоритм побудови середини відрізка.
- Алгоритм побудови бісектриси кута.
Методичний коментар
Вивчення нового матеріалу уроку можна провести у формі самостійної роботи учнів з підручником (при цьому варіанті учням слід пояснити зміст понять «розхил циркуля», радіус дуги, центр дуги і як описати дугу) або за наведеним вище планом під керівництвом учителя. В будь-якому разі основні акценти слід робити на таких моментах:
- побудови, які виконуються за допомогою циркуля і лінійки, мають певні обмеження;
- виконання навіть елементарних побудов потребує певної послідовності дій;
- послідовність дій при побудові зумовлена властивостями найпростіших геометричних фігур і пояснити її можна, посилаючись на означення, ознаки та властивості рівних фігур (найчастіше — трикутників).
Оскільки геометричні побудови в підручнику подано у вигляді опису розв'язання задач, необхідно після опрацювання кожної задачі узагальнити процес розв'язування, виокремлюючи послідовні його етапи, тобто скласти алгоритм.
Для більшої наочності і кращого засвоєння алгоритмів використовуємо таблицю № 22 «Геометричні побудови».
Таблиця № 22
Геометричні побудови
|
Дано |
Побудова (крок за кроком) |
|
|
1. Побудова трикутника за трьома (даними) сторонами |
||
|
|
Крок 1. АВ = а |
|
|
Крок 2. K1(A; b) і К2(В; с) перетинаються в точці С
|
||
|
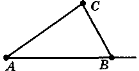
Крок 3. Відрізки АС і ВС. ∆АВС — шуканий
|
||
|
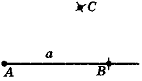
2. Побудова кута, що дорівнює даному |
||
|
|
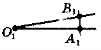
Крок 1. Промінь О1А1
|
|
|
Крок 2. Дуга К(О; R = OA); дуга К(О1; R = OA)
|
||
|
Крок 3. К(А1; R = АВ) — точка В1.
|
||
|
3. Побудова бісектриси кута |
||
|
|
Крок 1. Коло (О; R)
|
|
|
|
Крок 2. Дуги кола (A; R) і кола (В; R) перетинаються в точці С
|
|
|
|
Крок 3. Промінь ОС — бісектриса кута АОВ
|
|
|
4. Ділення відрізка навпіл (побудова середини, серединного перпендикуляра до відрізка) |
||
|
|
Крок 1. Дуги кола (A; R = AB) і кола (В; R = AB) перетинаються в точці С і D |
|
|
|
Крок 2. Пряма CD перетинає АВ в точці О АО = ВО (О — середина АВ) і CD |
|
VI. Первинне усвідомлення матеріалу
Усні вправи
- Опишіть, як поділити відрізок на чотири рівних відрізки.
- Опишіть, як поділити відрізок у відношенні 1 : 3.
- Опишіть, як поділити кут на чотири рівних частини.
- Опишіть, як поділити кут у відношенні 3 : 1.
Графічні вправи
За підручником задачі № 590, 591 (для розв'язання задачі побудувати бісектрису кута 180°), 594, 596, 599, 601.
Методичний коментар
Учні, ще до виконання побудов, мають попередньо скласти план своїх дій із посиланням на певний алгоритм, а під час побудови супроводжувати їх відповідним коментарем.
VII. Підсумки уроку
Який з вивчених на уроці алгоритмів слід використати, щоб побудувати прямокутний трикутник за двома катетами, а потім провести в ньому медіану до гіпотенузи?
VIII. Домашнє завдання
- § 20 — записати задачі № 1 – 4 у вигляді алгоритмів і вивчити ці алгоритми.
- Використовуючи вивчені алгоритми, розв'язати на окремому нерозлінованому аркуші задачі № 602, 604, 593 (це практична робота).
- На повторення: властивість медіани рівнобедреного трикутника, проведеної до основи; ознаки паралельності прямих (через співвідношення кутів, утворених при перетині даних прямих січною) № 7(б), с. 70.


про публікацію авторської розробки
Додати розробку