Розробка уроку на тему "Прямокутний трикутник"

Тема. Прямокутний трикутник

Мета: домогтися засвоєння учнями: означення прямокутного трикутника, назв його елементів, змісту властивості гострих кутів прямокутного трикутника і властивості сторін прямокутного трикутника, змісту ознак рівності прямокутних трикутників; сформувати вміння: викону­вати зображення прямокутного трикутника за даними задачі, за готовими зображенням або позначенням прямого кута прямокутного трикутника називати еле­менти прямокутного трикутника, відтворювати ознаки рівності прямокутних трикутників і застосовувати їх для розв'язування задач.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 15 «Прямокутний трикутник».

Хід уроку

І. Організаційний етап 

ІІ. Перевірка домашнього завдання 

Математичний   диктант   №   10

Варіант 1

1. У трикутниках ВОС і МАЕ сторони ВО і ОС рівні відповідно сторонам МА і АЕ. Чи обов'язково рівні ці трикутники?
2. Закінчіть речення: «Третя ознака рівності трикутни­ків — це ознака рівності за...»
3. У трикутниках ABC і РОТ сторони АВ і ВС дорівнюють відповідно сторонам РО і ОТ. Яка ще умова має бути виконаною, щоб ці трикутники були різними за третьою ознакою?
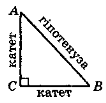
4. Доведіть рівність трикутників ABC і АМС за даними, позначеними на рис.  101.

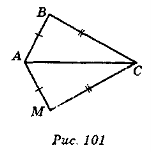
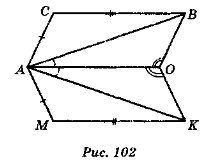
5. Доведіть рівність трикутників ABC і АМК за даними, позначеними на рис.  102.

Варіант 2

1. У трикутниках АСМ і ВЕК сторони АС і CM відповідно рівні сторонам BE і ЕК. Чи обов'язково ці трикутники рівні?
2. У трикутниках ABC і МКЕ сторони АВ і ВС дорівнюють відповідно сторонам МК і КЕ. Яка ще умова має бути виконаною, щоб ці трикутники були рівними за третьою ознакою?
3. Скільки пар рівних кутів треба знайти, щоб довести рівність двох трикутників:

а) за означенням;

б) за першою ознакою;

в) за другою ознакою;

г) за третьою ознакою?

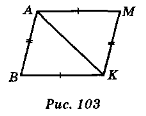
4. За даними рис. 103 доведіть рівність трикутників АМК і АВК.

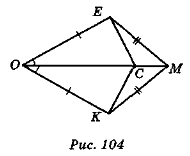
5. За даними рис. 104 доведіть рівність трикутників ЕСМ і КСМ.

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів 

Задача

Знайдіть невідомі кути трикутників на рис. 105. Які спільні риси мають ці трикутники?

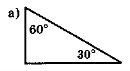
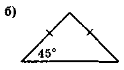
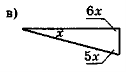
Рис. 105

Перелік спільних рис трикутників на рис. 105 приводить учнів до усвідомлення необхідності узагальнення відомостей про трикутники такого виду та вивчення їх особливостей. Ре­алізація цього завдання і є основною метою уроку.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

Обґрунтуйте рівність кожної пари трикутників (рис. 106).

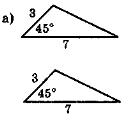
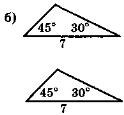
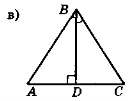
Рис. 106

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Означення прямокутного трикутника; елементи прямо­кутного трикутника.
2. Властивість сторін прямокутного трикутника.
3. Властивість гострих кутів прямокутного трикутника (та бісектрис прямокутного трикутника, проведених з вершин цих кутів).
4. Ознаки рівності прямокутних трикутників.

Методичний   коментар

Вивчення нового матеріалу здійснюється за традиційною схемою і супроводжується демонстрацією таблиці № 15 «Пря­мокутний трикутник».

Таблиця № 15

Прямокутний трикутник

VI. Первинне усвідомлення матеріалу

Усні   вправи

1. Назвіть прямокутні трикутники, зображені на рис. 107. У кожному трикутнику назвіть катети і гіпотенузу.

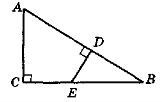
Рис. 107

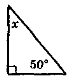
2. Знайдіть величину х і градусну міру кутів у кожному трикутнику (рис.  108).

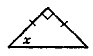
Рис. 108

VII. Вироблення ВМІНЬ

Письмові   вправи

Задачі на закріплення матеріалу уроку можна умовно поді­лити на такі групи:

а) задачі на застосування властивості гострих кутів трикутника (№ 442, 443, 445);

б) задачі на застосування властивості бісектрис гострих кутів прямокутного трикутника (№ 449 — опорна задача, № 462 —
на застосування властивості бісектрис гострих кутів прямокутного трикутника).

Методичний   коментар

При роботі над виробленням умінь застосовувати влас­тивість гострих кутів прямокутного трикутника слід одразу попереджати традиційні помилки учнів: при обчисленні градусних мір гострих кутів прямокутних трикутників не треба використовувати теорему про суму кутів трикутника в загальному вигляді, а слід спиратися саме на твердження про те, що сума гострих кутів прямокутного трикутника дорівнює 90°.

Щодо властивості бісектрис гострих кутів прямокутно­го трикутника, то це твердження можна вивчити на етапі формування знань, або ж розглядати як опорну задачу (як це і робиться в підручнику), або як особливий випадок (для прямокутного трикутника) загального співвідношення між кутом трикутника і кутом між бісектрисами двох інших кутів трикутника (рис. 109).

АА₁ і СС₁  — бісектриси кутів А і С трикутника ABC ;

В = β, AOC = α, α = 90° + α' = 90°  – .

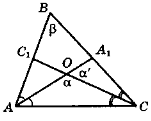
Рис. 109

VIII. Підсумки уроку

Запитання до класу

1. Чи може в прямокутному трикутнику бути дві гіпотену­зи?
2. Чи   може  прямокутний  трикутник  бути рівностороннім?
3. Чи може прямокутний трикутник бути рівнобедреним?
4. Визначте  вид  трикутника,   якщо  відомо,   що  дві  його сторони пристають до висот.
5. Визначте вид трикутника, якщо відомо, що тільки одна його висота проходить усередині цього трикутника.

IX. Домашнє завдання

1. § 15 — вивчити означення, властивості та ознаки рів­ності прямокутних трикутників.
2. Письмово: № 448, 463, 456.
3. На повторення: № 4 (б), с. 100 (задачі за готовими ри­сунками).