Розробка уроку «Розв'язування найпростіших тригонометричних рівнянь»

Тема урока: Решение простейших тригонометрических уравнений

Цели урока:

- ознакомить с выведением  общих формул решения уравнений вида cos x=a, sin x=a, tg x=a,ctg x=a;

- сформировать умение использовать их при решении уравнений;

- создать условия для развития критического мышления;

- развивать коммуникативные способности учащихся, навыки сотрудничества.

Тип урока: Урок «открытия» нового знания

Оборудование: Проектор, компьютер, раздаточный материал

Форма работы: Фронтальная, групповая, индивидуальная

Девиз урока: Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду. Л. Толстой

 

Ход урока

1. Мотивационный этап

Задумывались ли вы ребята, с какой целью пришли сегодня на урок? Я постараюсь вам помочь в выборе. На партах вы видите список личностных целей. Выберите из этого списка 1-2 цели. Напишите на полях в тетради их номер. Постарайтесь поработать на эти цели в течение всего урока.

 

Личностные цели:

2) научиться легко выполнять математические операции;

3) научиться точно и грамотно излагать свои мысли;

4) научиться ничего не принимать на веру, анализировать, делать выводы;

5) научиться применять формулы корней тригонометрических уравнений при их решении;

6) активно работать на уроке;

7) получить удовольствие от урока;

8) получить хорошую отметку.

 

Ребята, в современной жизни очень важно уметь вступать в диалог и, уважая мнение другого, высказать собственное «иное» мнение с аргументацией, а также уметь делать самооценку. Поэтому сегодня вы сами будете оценивать результаты своей деятельности. За каждый правильный ответ и результативное выступление у доски вы на полях тетради ставите себе 1 балл, а в конце урока с помощью специальной шкалы переведете их в отметку.

 

2. Актуализация знаний

 

1. Вычислите:

arccos + arcsin

arcsin (-) + arccos (-)

arctg (-1)+arcctg(-1)

 

2. Вычислите
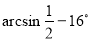
3. Найдите значение
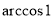
4. Выполните действия:

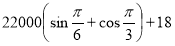
Учитель пишет ответы на доске в строку 14022018

Посмотрите, что получилось?

Тема нашего урока –  решение простейших тригонометрических уравнений.

Мы с вами на прошлом уроке учились решать уравнения с помощью единичной окружности и графическим способом.

3. Выявление места и причины затруднения

Первый ряд, у вас на карточке уравнение и график функции .

Второй ряд, у вас на карточке уравнение и eдиничная окружность.

Третий ряд, у вас на карточке уравнение и график функции , и единичная окружность.

Решите эти уравнения, у вас есть три  минуты.

Почему не вышло ни одним из способов решить уравнение третьему ряду? (Не знаем, как решить уравнения, используя числовую окружность или график)

4. Построение проекта выхода из затруднения

Чем это задание отличается от предыдущих?

(Чтобы решить уравнение cosx = , нам нужно найти на числовой окружности точки с абсциссой  и записать, каким числам  t они соответствуют. Абсциссу  имеют точки М и Р, но каким значениям  t они соответствуют, мы не знаем .В уравнениях  cos t = ;  sin t = - такие числа мы знали. Поэтому решить данные уравнения мы не можем.)

 

-Какая же цель урока?

 (вывести общие формулы решения уравнений).

5. Реализация построенного проекта. ( «Открытие»  нового знания)

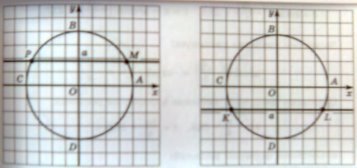
-Что нам может помочь при решении уравнений вида cos t =а, sin t =а? (единичная числовая окружность)                

- Рассмотрим уравнение вида cos t =а и отметим на числовой окружности точки, абсциссы которых равны а .

- Сколько таких точек имеем? (две)           

- Пусть это точки М и N. Что про эти точки можно сказать?

(Они симметричны относительно оси абсцисс)

- Равны ли величины дуг АМ и АN?

(Они равны по модулю, но противоположны по знаку)

 

          

 

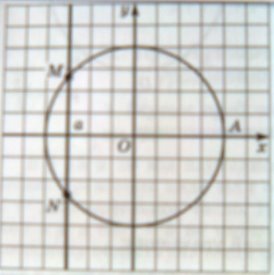
- Какому числу соответствует точка М ?

Если учащиеся затрудняются с ответом, предлагаю подсказку.

- Верно ли, что точка М соответствует числу, косинус которого равен а. Как называется такое число? (arccos а)

-А еще каким числам соответствует  точка М?  (всем числам вида

 arccos а+2к)

- Какому числу соответствует точка N ? ( числу  -arccos а и всем числам вида  -arccos а+2к)

- Следовательно, как можно записать решения уравнения  cos t =а, где ?

 

t = arccos а+2k; kZ.

 

Общая формула решения уравнений вида cos t =а , где  .

- Самостоятельно выведите формулу для решения уравнения sin t =а, 

 где  (работа в группах).

- Составьте план действий.

  1. Отметить на числовой окружности точки, ординаты которых равны а.

  2. Определить, каким числам соответствуют данные точки.

  3. Попытаться записать решения уравнения sin t =а в виде формулы. 

 

- Какие правила надо помнить при работе в группах, чтобы работа была результативной?

( Каждый может высказать свое мнение, остальные должны выслушать, каждый должен сделать свой вклад в работу группы, обсуждать надо тихо, не мешая всем остальным)

 

По окончании работы группы представляют свои результаты, одна из групп объясняет вывод формулы, остальные – дополняют, уточняют.

 

 

t = arcsin а +2k,     t = - arcsin а +2k;  kZ.

 

Общая формула решения уравнений вида sin t =а  , где  .

- Формулы  t = arcsin а +2k,     t = - arcsin а +2k;  kZ можно объединить общей формулой вида

t =(-1)п arcsin а +п ,  пZ

 

t = arcsin а +2k, 

t = - arcsin а +2k;  kZ.

Эти формулы можно записать в следующем виде:

 

t = arcsin а +2k, 

t = - arcsin а +(2k+1);  kZ.

 

Если перед arcsin а стоит знак «+», то у числа множителем является четное число 2k, если же перед arcsin а стоит знак «-», то у числа множителем является нечетное число 2k +1.      Следовательно, 

t =(-1)^п arcsin а +п ,  пZ.

При четном  п ( п=2к) имеем   t = arcsin а +2k ,

при  нечетном   п ( п=2к+1) имеем  t = - arcsin а +2k;  kZ.

 

 

Аналогично рассуждая можно вывести формулы и для остальных уравнений

 

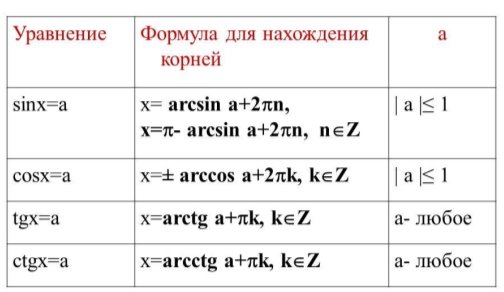
Мы достигли поставленной цели? (да, вывели формулы решения уравнений)

- Можем ли мы теперь при решении уравнений обходиться без числовой окружности? (да, достаточно знать формулы)

6. Первичное закрепление во внешней речи

Решаем у доски №353(1), 364(6), 371(1.3)

Обратите внимание, что иногда уравнение необходимо привести к простейшему виду.

- Какой следующий этап работы? Что необходимо сделать, чтобы понять, усвоили вы тему или нет?

(выполнить самостоятельную работу)

 

 

7. Самостоятельная работа с самопроверкой по эталону.

Задание на карточках

cos х = ;

 tg х = -1;

sin х =.

После завершения работы учащиеся сравнивают свои решения с эталоном.

 

cos х = ,    х= arccos +2k;    kZ

tg х = -1 x= arctg (-1) +k;  kZ x=-arctg 1+k;   kZ x= +k;   kZ

sin х =,   решений нет,  т.к.          1

 

- Кто решал данные уравнения?

- У кого они вызвали затруднение?

- Где и почему допустили ошибку?

- Какие формулы использовали при решении уравнений?

- Кто решил все уравнения верно? Молодцы!

8. Рефлексия деятельности на уроке

-Какая цель стояла перед вами?

- Удалось достичь цели урока?

- Какие знания помогали нам в достижении цели?

- Для чего нам нужно новое знание?

- Проанализируйте и оцените свою работу на уроке.

 

9. Домашнее задание

 §25, 26, 27

№354(4), 365(1), 371(2.4) на 9 баллов

№354(4), 365(1),373(1,7) на 11баллов

* вывести формулы корней уравнений через графики тригонометрических функций

 

Шкала

10б – 10

9б– 9  

8б – 8

7б – 7

6б – 6

5б – 5

4б – 4

3б – 3