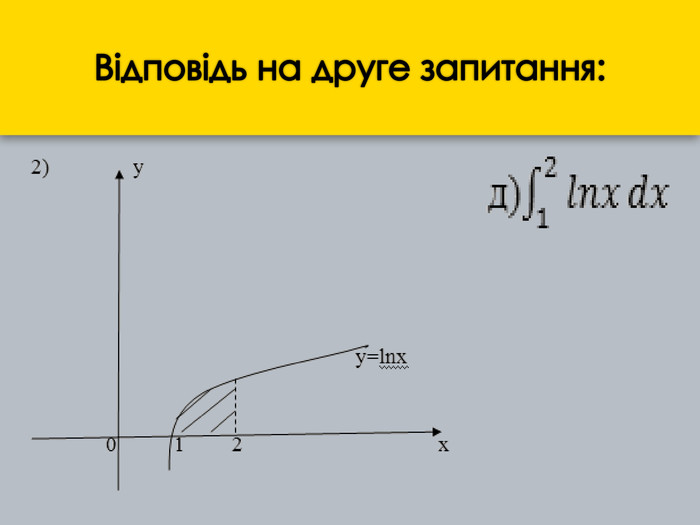
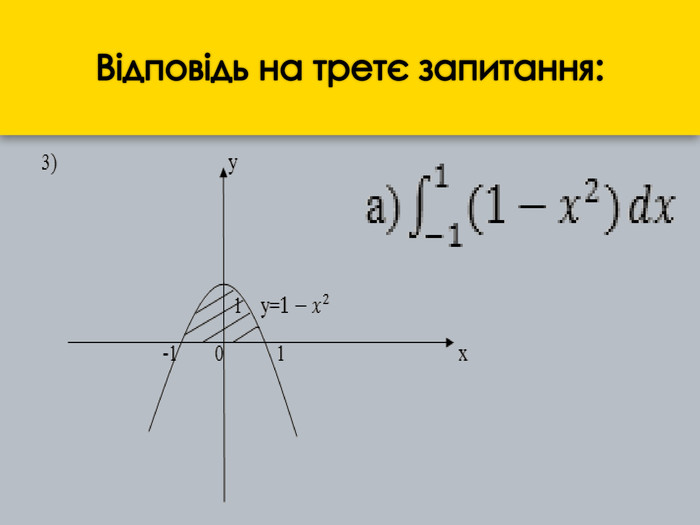
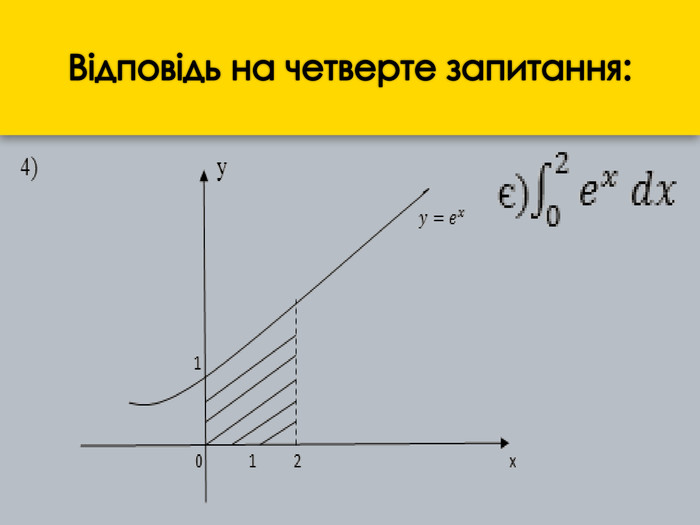
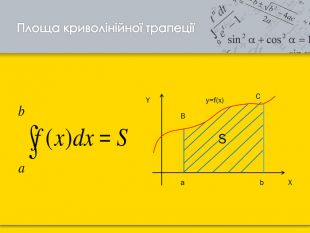
Розробка уроку та наукові матеріали виступів учнів на тему: " Застосування визначеного інтегралу."
У цій розробці Ви зможете ознайомитися з гарно підібраними для виступу вчителя матеріалів та дуже цікаві та науково-глибокі матеріали груп учнів з підібраними домашніми завданнями.
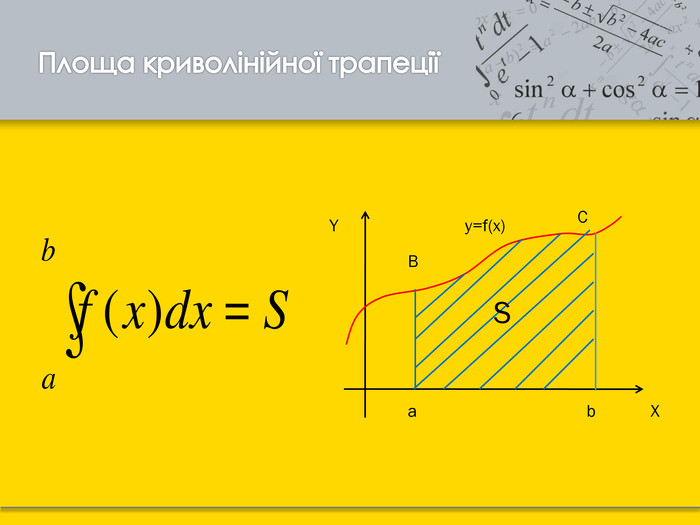
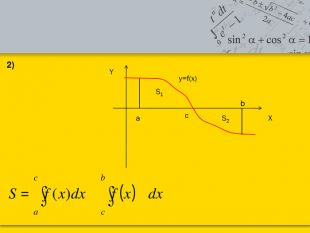
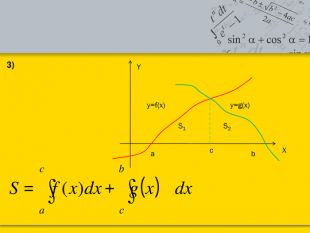
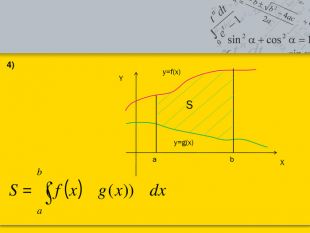
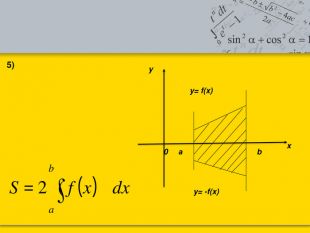
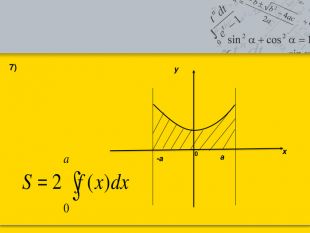
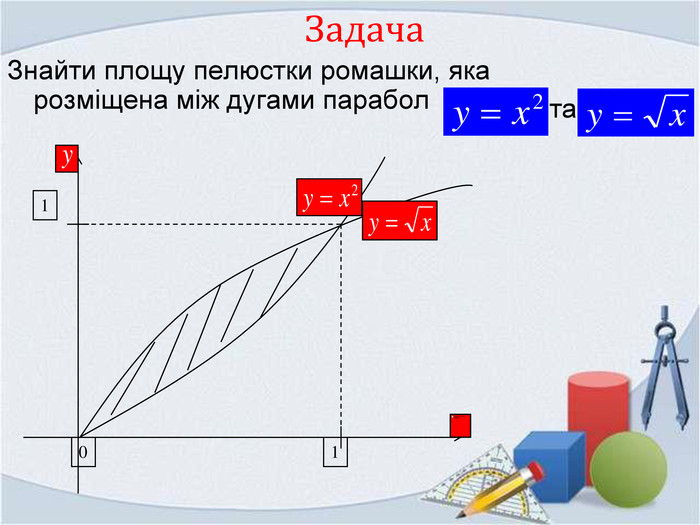
Тема: «Застосування визначеного інтеграла до знаходження площі криволінійної трапеції.»
Мета: поглибити і розширити знання учнів про визначений інтеграл, продовжити формування навичок знаходити визначений інтеграл. Сприяти розвитку творчих здібностей учнів, формувати їх пізнавальний досвід, вміння виступати перед аудиторією. Розвивати логічне мислення, інтелектуальні здібності учнів.
Тип уроку: застосування знань, умінь та навичок.
Обладнання : мультимедійний проектор.
Хід уроку
І. Організаційний момент
Уявіть, що у ваших долоньках - дрібка гарного настрою. Поділіться ним, щоб
зробити день приємнішим для всіх, хто зараз поряд з вами.Почнімо наш урок. Девіз нашого уроку(хором) : «Вигадуй, пробуй, твори! Розум, фантазію прояви!»
Розпочинаємо урок, який проводимо між представниками різних творчих груп «науковцями» , «фізиками», «практиками» та «істориками».
ІІ. Мотивація навчальної діяльності, повідомлення теми й мети уроку
ІІІ. Актуалізація й систематизація опорних знань , умінь та навичок
- Перевірка й повторення базових знань
|
Функція |
хⁿ |
k |
sinx |
cosx |
|
|
|
Загальний вигляд первісної |
|
|
|
|
|
|
- Продовжи речення:
- що таке первісна?
- чому дорівнює значення визначеного інтеграла на відрізку [a;b]?
- Розв’язужи завдання. Знайти визначений інтеграл.
|
|
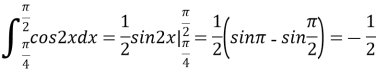
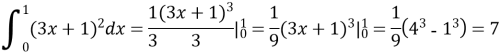
IV. Поглиблення і розширення знань та їх застосування
А зараз давайте з ясуємо як саме ми можемо застосувати визначений інтеграл у геометрії при знаходженні площ фігур; у фізиці в задачах на рух, на роботу на знаходження маси тіла.
Слово надаю творчій групі «Науковців».
(Творча група підготувала презентацію, роздатковий матеріал, та домашнє завдання згідно з розглянутих задач)
Слова надається групі «Фізики».
(Творча група підготувала презентацію, роздатковий матеріал, та домашнє завдання згідно з розглянутих задач)
Слово надається групі «Практики».
(Творча група підготувала презентацію та домашнє завдання згідно з розглянутих задач)
Слово надається групі «Історики».
(Творча група підготувала презентацію та домашнє завдання згідно з розглянутих задач)
Самостійна робота(роздається кожній групі)
Хто швидше?
Обчислити інтеграли:
1) 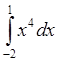 ; 2)
; 2) 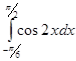 ; 3)
; 3) ![]() ;
;
4) 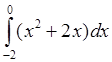 ; 5)
; 5)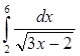 ; 6)
; 6) 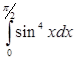 ;
;
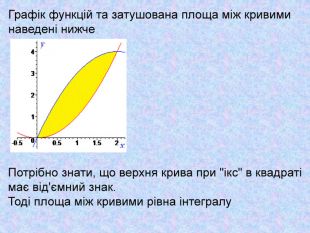
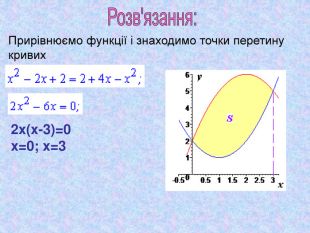
Обчисліть площу фігури, обмеженої лініями:
а) у = x2 - 2х + 3, x + у = 5;
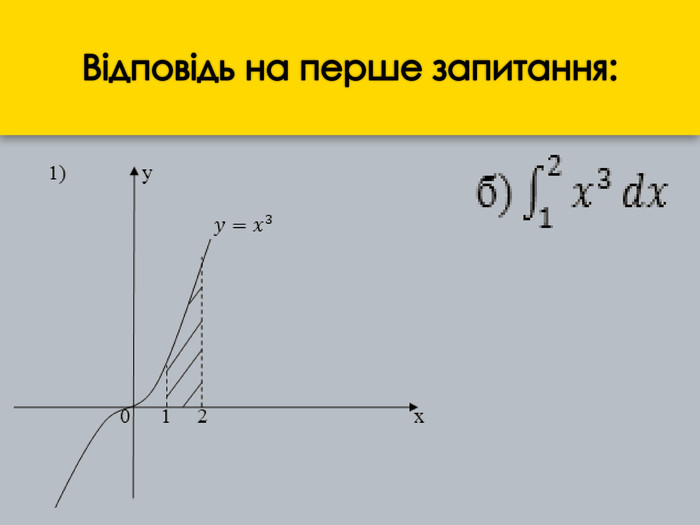
б) у =![]() , у = 2 - x2, x = -1, у = 0;
, у = 2 - x2, x = -1, у = 0;
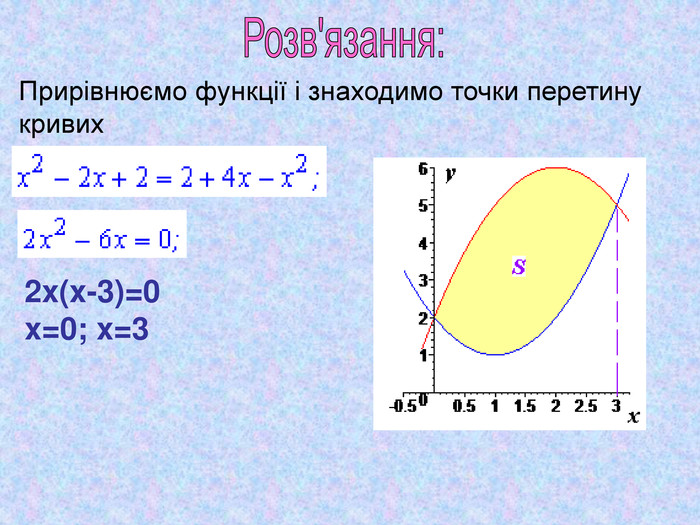
в) у = -х2 + 6х – 2; y = х2 - 2х + 4.
V. Підсумок уроку.
VI. Домашнє завдання.
Виконати домашні завдання кожної групи.
1. Знайти площу фігури, обмеженою лініями
a) f( x ) = 2 х – х 2 і віссю абсцисс
Розв’язання: Графік функції f(x) = 2x - х2 парабола. Вершина: (1; 1).
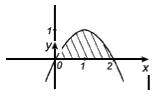
![]()
Відповідь:![]()
б) ![]()
Розв’язання: Графік функції ![]() – пряма.
– пряма.
2.
|
x |
0 |
4 |
|
y |
0 |
2 |
Функція ![]() є оберненою функції y = х 2 на проміжку [0; +∞).
є оберненою функції y = х 2 на проміжку [0; +∞).
|
x |
0 |
1 |
4 |
|
y |
0 |
1 |
2 |
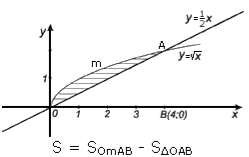
Межі інтегрування вказані в таблицях значень функцій.
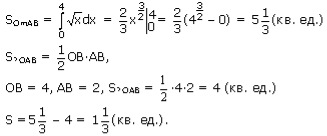
Відповідь:![]() ( кв . од .).
( кв . од .).
УРОК 30
Тема уроку. Інтеграл у фізиці та техніці.
Мета уроку. Познайомити учнів із застосуванням інтеграла у фізиці, техніці.
І. Перевірка домашнього завдання.
1. Перевірте правильність виконання домашніх вправ.
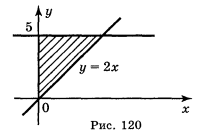 № 12 (розділ ІХ). 1) Рис. 120.
№ 12 (розділ ІХ). 1) Рис. 120.
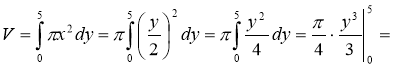
![]() .
.
 Відповідь: 10
Відповідь: 10 ![]() π.
π.
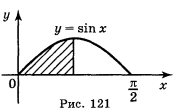
2) Рис. 121.
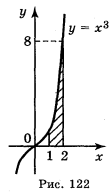
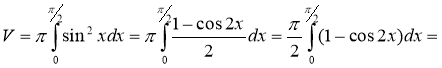
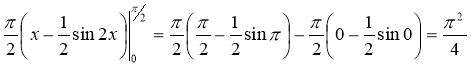 .
.
Відповідь: ![]() .
.
3) Рис. 122.
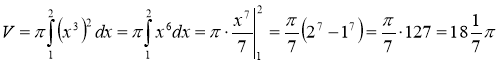 Відповідь: 18
Відповідь: 18![]() π.
π.
2. Фронтальна бесіда за запитаннями № 16—17 із «Запитання і завдання для повторення» із розділу IX.
II. Сприймання і усвідомлення матеріалу про застосування інтеграла у фізиці.
Інтеграл широко використовується у фізиці. Розглянемо таблицю 11.
Коментарі до таблиці
1. Припустимо, що точка рухається по прямій (по осі ОХ) і нам відома швидкість цієї точки. Як знайти переміщення точки за проміжок часу [t1; t2]?
Розглянемо відрізок часу [t; t + Δt] і будемо вважати швидкість на цьому відрізку постійною. Тоді одержимо Δs(t) = v(t)·Δt, звідси
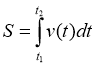
2. Нехай тіло рухається по осі ОХ, в кожній точці якої прикладена деяка сила F = F(x). Обчислимо роботу, яку треба виконати при переміщенні із точки х1 в точку x2. На маленькому відрізку шляху від точки x до точки x + Δx можна вважати силу постійною, яка дорівнює F(x). Тоді ΔА(x) = F(x)Δx. Звідси одержуємо, що всю роботу на відрізку [x1; x2] можна записати у вигляді інтеграла:
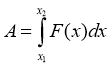
3. Розглянемо задачу обчислення маси неоднорідного стержня, якщо нам відомо, як змінюється його лінійна густина р(х). Візьмемо відрізок [x; x+Δx]. Вважаючи, що на цьому відрізку густина постійна, матимемо Δm(x) = р(x)Δx; звідси
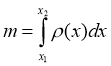
4. Поставимо задачу обчислити заряд q, що переноситься за проміжок часу [t1; t2] через переріз провідника. Нехай задано закон зміни струму І = I(t) в залежності від часу. Тоді на малому проміжку часу [t; t + Δt] можна вважати силу струму постійною, яка дорівнює I(t), a Δq(x) = I(t) · Δt і, отже
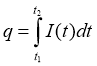
Виконання вправ № 13 (1; 3), № 15, 18, 19, 5, 7 із Вправ до розділу IX.
III. Підведення підсумків уроку.
IV. Домашнє завдання.
Розділ IX § 4 (6); Запитання і завдання для повторення розділу IX № 13.
Вправи № 13 (2; 4), 17, 6.

1
Роганін Алгебра 11 клас, урок 30
1.Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = – х2 + 2х + 3 навколо вісі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м3. Яка масу каменя використали на виготовлення цього жертовника стародавні майстри?
2.Хто запропонував термін ,,Інтеграл,, і в якому році ?


про публікацію авторської розробки
Додати розробку

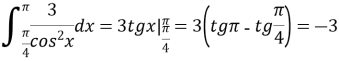

![Криволінійною трапецією називається фігура, обмежена графіком невід'ємної і неперервної на відрізку [a;b] функції, віссю Ох і прямими x=а та x=b. Криволінійна трапеція та її площа Криволінійною трапецією називається фігура, обмежена графіком невід'ємної і неперервної на відрізку [a;b] функції, віссю Ох і прямими x=а та x=b. Криволінійна трапеція та її площа](/uploads/files/236342/80453/85995_images/2.jpg)