Розділ 5. Елементи теорії ймовірності та математичної статистики.

Т.5.1. Елементи комбінаторики. Комбінаторні правила суми та добутку. Перестановки, розміщення, комбінації.

Мета заняття: ознайомити студентів з тим, що вивчає комбінаторика, і комбінаторними правилами суми та добутку, ознайомити студентів з формулами для обчислення числа перестановок, розміщень і комбінацій; учити використовувати ці формули під час розв’язування задач; дати схему розв’язування комбінаторних задач; розвивати логічне мислення, пам’ять, увагу; виховувати математичну грамотність, наполегливість, акуратність.

Тип заняття: засвоєння нових знань.

Обладнання:  роздатковий матеріал

Хід заняття І. Організаційний етап.

ІІ. Формулювання теми, мети й завдань уроку, мотивація навчальної діяльності.

У житті часто доводиться що-небудь обирати з великої кількості всіляких варіантів. Наприклад, 

ü    скількома способами можна розташовувати в турнірній таблиці 10 футбольних команд, якщо жодні дві з них не набрали порівну очок?

ü    скількома способами можна скласти розклад на день із 4 навчальних предметів для однієї групи, якщо в групі вивчається 9 предметів?

ü    Скільки п’ятицифрових чисел можна скласти із цифр 1,2,3,4,5, якщо цифри в числі не повторюються?

Для таких задач існують загальні методи розв’язування, що вивчає комбінаторика як розділ математики.

ІІІ. Сприйняття та усвідомлення нового матеріалу.

Шкільна лекція:

1. Елементи комбінаторики. Комбінаторні правила суми й добутку.

(Згадати поняття множини, елементів множини)

Скінченна упорядкована множина – така множина, для якої визначений порядок розміщення її елементів.

Комбінаторика – розділ математики присвячений розв’язанню задач про вибір і розміщення елементів скінченої множини, відповідно до заданих правил.

Ці правила визначають спосіб побудови деякої конструкції – комбінаторної сполуки.

В основі класичної комбінаторики лежать комбінаторні правила суми та добутку.

Наприклад (правило суми) – на тарілці лежать 5 яблук і 9 груш. Один плід можна обрати 5+9=14 (способами).

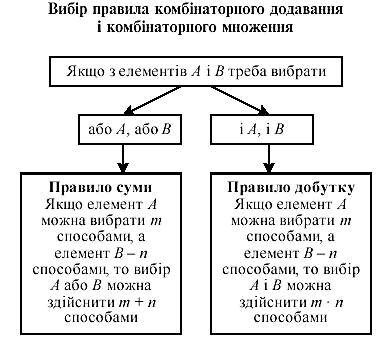
Наприклад (правило добутку) – із 6 видів конвертів без марок і 5 марок один конверт і одну марку можна вибрати 6(способами).

Вправа 1.У групі 15 хлопців і 12 дівчат. Скількома способами можна вибрати : 1) хлопця;

2)      дівчину;

3)      одного студента цієї групи; 4) двох студентів – хлопця й дівчину.

Розв’язання

1)                  Хлопця можна вибрати 15 способами;

2)                  дівчину можна вибрати 12 способами;

3)                  за правилом суми або дівчину або хлопця можна вибрати 15+12 =27 способами;

4)                  за правилом добутку вибрати двох студентів  - хлопця й дівчину – можна 15·12=180 способами. Відповідь: 1)15; 2)12; 3) 27;4) 180 способами.

Вправа 2. Скількома способами можна пошити триколірний прапор, якщо є тканини 5 різних кольорів?

Розв’язання

Перший колір можна вибрати п’ятьма способами, другий – чотирма, третій – трьома. За правилом добутку триколірний прапор можна зшити 5·4·3=60 способами. Відповідь: 60.

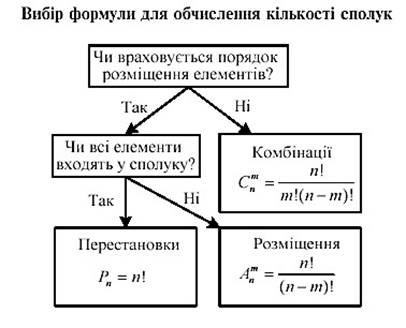
2. Перестановки, розміщення ,комбінації.

Означення. Факторіалом називають добуток n послідовних натуральних чисел (n – факторіал). 0!=1, 1!=1.

Наприклад, 5!=1·2·3·4·5=120,  2!=1·2=2, 4!=1·2·3·4=24.

Означення. Перестановкою з n елементів називають будь-яку впорядковану множину з n елементів.

В даній формулі кожен елемент, що входить у комбінацію поданий у єдиному екземплярі.

Повернемося до задачі, яку ми розглядали на початку заняття. 

ü Скільки п’ятицифрових чисел можна скласти із цифр 1,2,3,4,5, якщо цифри в числі не повторюються?

Отже, кількість таких чисел дорівнює  

Означення. Розміщенням з n елементів по k називають будь-яку впорядковану множину з  елементів n- елементної множини.

Розглянемо задачу. Скільки трицифрових чисел можна скласти з цифр 1,2,3,4,5 за умови, що цифри не повторюються. 

Отже, маємо розміщення з 5 по 3 елементи:  

Означення. Комбінацією без повторень з n елементів по k називають будь-яку k- елементну підмножину  n – елементної множини.

Розглянемо задачу. Скількома способами  можна вибрати дві різні цифри із цифр 1,2,3,4,5?

У цій задачі не має значення порядок розміщення двох цифр, які вибираємо із даних п’яти цифр, тобто способів вибору цифр буде .

Під час розв’язування комбінаторних задач зручно користуватися схемою:

 ІV. Осмислення нового матеріалу. 

Колективне розв’язування вправ.

Вправа 1.  Скількома способами можна скласти список із 6 учнів?

Оскільки порядок розміщення елементів враховується і всі елементи входять до сполуки, то

.

Відповідь: 720 способами.

Вправа 2.   Скількома способами можна розмістити 8 осіб за столом, біля якого стоїть 8 стільців?

Розв’язання

Оскільки порядок розміщення елементів враховується і всі елементи входять до сполуки, то  (способами) 

Відповідь: способами.

Вправа 3.   Скільки існує трицифрових чисел, у яких всі цифри непарні й різні.

Розв’язання

Усього непарних цифр 5. Оскільки порядок враховується й до сполуки входять не всі цифри, а тільки три, то таких чисел буде. .

Відповідь: 60.

Вправа 4.   Скільки існує трицифрових чисел, у яких всі цифри парні й різні.

Розв’язання

Усього парних цифр 5. Тоді можна скласти трицифрових чисел усього  , але серед них будуть і ті ,що мають нуль на першому місці. Таких «неправильних чисел» буде . Отже, чисел, що нас

цікавлять, буде  

Відповідь: 48.

Вправа 5.   Із 3 яблук і 7 бананів треба приготувати десерт із 5 фруктів, у який входило б хоча б  одне яблуко. Скількома способами це можна зробити?

Розв’язання

1)  Скількома способами можна приготувати десерт із 1 яблука і 4 бананів? Яке правило слід застосувати? (Правило добутку)

2)  Скількома способами можна приготувати десерт із 2 яблук і 3 бананів?

.

3)  Скількома способами можна приготувати десерт із 3 яблук і 2 бананів?

4)  Скількома способами можна приготувати даний десерт? Яке правило при цьому слід застосувати?

105+105+21=231 (сп.) Відповідь: 231 спосіб.

V. Підбиття підсумків заняття

VІ. Домашнє завдання.

Опрацювати конспект, вивчити означення та формули.

Виконати вправи:

1.            У підрозділі 60 солдат і 5 офіцерів. Скількома способами можна виділити наряд, який складається із трьох солдат і одного офіцера?

2.            4. Із 10 троянд і 8 жоржин треба скласти букет так, щоб в ньому були 2 троянди і 3 жоржини. Скількома способами можна скласти букет?

3.            5. Із семи бігунів і трьох стрибунів треба скласти команду із 5 чоловік, в яку б входив хоч би один стрибун. Скількома способами це можна зробити?

4.            До складу експедиції входять 5 юнаків і 3 дівчини. Для участі у розкопках прийшло три запрошення. Скількома способами можна розподілити ці запрошення, щоб туди потрапила хоча б 1 дівчина?