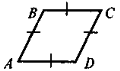Розробка уроку з геометрії "Прямокутник"

Тема. Прямокутник

Мета: сформувати в учнів уявлення про прямокутник як один із видів паралелограма; розглянути властивості та ознаки прямокутника; сформувати вміння й навички застосовувати властивості та ознаки прямокутника під час розв'язування задач.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект «Прямокутник».

Хід уроку

I. Організаційний етап

 

II. Перевірка домашнього завдання

Учитель збирає зошити учнів із виконаною домашньою самостій­ною роботою на перевірку. У разі потреби на цьому етапі проводиться стислий аналіз виконаних завдань, та учні, які припустилися великої кількості помилок, отримують завдання для корекційної роботи.

 

III. Формулювання мети і завдань уроку

З метою створення умов для усвідомленого сприйняття учнями ма­теріалу уроку пропонуємо їм розв'язати логічну вправу.

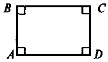
Порівняйте фігури на рисунку 1 (за різними критеріями). Яка із фігур «зайва»?

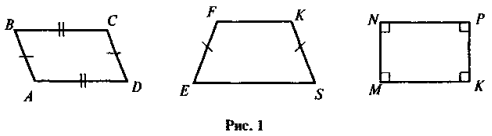
Після успішного виконання завдань (зрозуміло, що «зайвим» є чо­тирикутник EFKS, у якого на відміну від двох інших чотирикутників є лише дві паралельні сторони) учитель звертає увагу учнів на той факт, що паралелограм MNPK є особливим випадком паралелограма, бо, крім паралельності протилежних сторін, має прямі кути. Таким чи­ном, виділяється новий об'єкт, вивчення якого за загальною схемою і становить основну дидактичну мету.

 

IV. Актуалізація опорних знань та вмінь

 

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення прямокутника.
2. Властивості прямокутника.
3. Ознаки прямокутника.

 

 

 

 

 

 

 

с	Прямокутник Означення. Паралелограм, усі кути якого прямі, називається прямокутником
	Властивості	Ознаки
	1. Усі властивості паралелограма 2. Якщо ABCD - прямокутник, то АС = BD. (Діагоналі прямокутника рівні)	1. Якщо ABCD — парале­лограм і А = 90°, то ABCD — прямокутник Якщо ABCD — паралело­грам і АС = BD, то ABCD — прямокутник. (Якщо діагоналі паралело­грама рівні, то цей пара­лелограм — прямокутник)
	3. Якщо ABCD — прямокутник, (AD > CD), AC і BD — діагоналі, то AOB = 2ACB
	4. Якщо ABCD — прямокутник і точ­ка М — середина ВС, то ОМВС. ОМ = АВ.
	(Відрізок, що з'єд­нує середину сто­рони прямокутника з точкою перетину діагоналей, перпен­дикулярний до цієї сторони і дорівнює половині суміжної сторони)

 

VII. Формування первинних умінь

З метою закріплення знань учнів щодо означення, властивостей та ознак прямокутника спочатку доцільно розв'язати усні задачі.

Виконання усних вправ

1. У прямокутнику ABCD А В = 8 см, ВС = 5 см. Знайдіть:

а) відстань від точки С до сторони AD;

б) відстань між прямими АВ і CD.

2. Чи може діагональ прямокутника до­рівнювати   його   стороні?   Чи   може діагональ ромба дорівнювати його сто­роні?
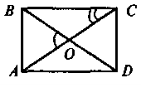
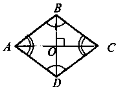
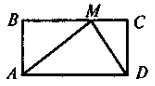
3. а) Укажіть (див. рис. 2) відрізки, кути,
   трикутники.

б) AOD = 142°. Знайдіть OCD і OBC.

в) Р_ВОС = 16 см, АС · BD = 100. Знайдіть AD.

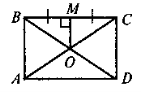
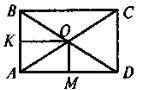
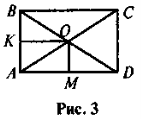4. За рисунком 3 розв'яжіть задачі:

а) КО = 4 см, ОМ = 2 см. Знайдіть P_ABCD.

б) AOD = 120°, BD = 2 см. Знайдіть Р_ОВС.

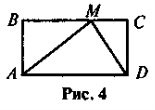
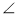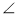5. У прямокутнику ABCD (рис. 4) BAM =DAM, 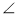MDC = 30°, АВ = 1, ВС = 3. Знайдіть P_ABМD.

Після закріплення знань означення, властивостей та ознак прямо­кутника доцільно розв'язати типові задачі на застосування цих знань.

Виконання письмових вправ

1. Знайдіть периметр прямокутника ABCD, якщо АС =15 см, а пери­метр трикутника ABC дорівнює 36 см.
2. У прямокутнику ABCD 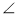BAC = 65°. Знайдіть кут між діагоналями прямокутника.
3. Діагоналі прямокутника ABCD перетинаються в точці О, причому 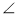COD = 60°, CD = 8 см. Знайдіть довжину діагоналі.
4. Точка перетину діагоналей прямокутника віддалена від двох його сторін на 3 см і 4 см. Знайдіть периметр прямокутника.

 

VII. Підсумки уроку

VIII. Домашнє завдання

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №                                                        Тема. Прямокутник

Дата:

Клас: 8-А, 8-Б

Предмет: геометрія

Мета: сформувати в учнів уявлення про прямокутник як один із видів паралелограма; розглянути властивості та ознаки прямокутника; сформувати вміння й навички застосовувати властивості та ознаки прямокутника під час розв'язування задач.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

III. Формулювання мети і завдань уроку

З метою створення умов для усвідомленого сприйняття учнями ма­теріалу уроку пропонуємо їм розв'язати логічну вправу.

Порівняйте фігури на рисунку (за різними критеріями). Яка із фігур «зайва»?

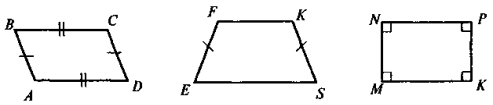
IV. Актуалізація опорних знань та вмінь

Для свідомого розуміння та подальшого засвоєння учнями змісту означення, властивостей та ознак прямокутника слід активізувати знання і вміння учнів щодо означення, властивостей та ознак парале­лограма; означення прямокутного трикутника та ознак рівності пря­мокутних трикутників; означення, властивостей кутів та ознак рівнобедреного трикутника.

V. Засвоєння знань

План вивчення нового матеріалу

4.               Означення прямокутника.
5.               Властивості прямокутника.
6.               Ознаки прямокутника.

Повний перелік тверджень, що стосуються прямокутника, які ба­жано вивчити з восьмикласниками, міститься в конспекті «Прямо­кутник».

с	Прямокутник Означення. Паралелограм, усі кути якого прямі, називається прямокутником
	Властивості	Ознаки
	1. Усі властивості паралелограма 2. Якщо ABCD - прямокутник, то АС = BD. (Діагоналі прямокутника рівні)	1. Якщо ABCD — парале­лограм і А = 90°, то ABCD — прямокутник Якщо ABCD — паралело­грам і АС = BD, то ABCD — прямокутник. (Якщо діагоналі паралело­грама рівні, то цей пара­лелограм — прямокутник)
	3. Якщо ABCD — прямокутник, (AD > CD), AC і BD — діагоналі, то AOB = 2ACB
	4. Якщо ABCD — прямокутник і точ­ка М — середина ВС, то ОМВС. ОМ = АВ.
	(Відрізок, що з'єд­нує середину сто­рони прямокутника з точкою перетину діагоналей, перпен­дикулярний до цієї сторони і дорівнює половині суміжної сторони)

 

VII. Формування первинних умінь

З метою закріплення знань учнів щодо означення, властивостей та ознак прямокутника спочатку доцільно розв'язати усні задачі.

Виконання усних вправ

1. У прямокутнику ABCD АВ = 8 см, ВС = 5 см. Знайдіть:

а) відстань від точки С до сторони AD;

б) відстань між прямими АВ і CD.

2. Чи може діагональ прямокутника до­рівнювати   його   стороні?  

3.За рисунком розв'яжіть задачі:

а) КО = 4 см, ОМ = 2 см. Знайдіть P_ABCD.

б) AOD = 120°, BD = 2 см. Знайдіть Р_ОВС.

4.У прямокутнику ABCD BAM =DAM, MDC = 30°, АВ = 1,

ВС = 3. Знайдіть P_ABМD.

Виконання письмових вправ

1. Знайдіть периметр прямокутника ABCD, якщо АС =15 см, а пери­метр трикутника ABC дорівнює 36 см.

2. У прямокутнику ABCD BAC = 65°. Знайдіть кут між діагоналями прямокутника.

3. Діагоналі прямокутника ABCD перетинаються в точці О, причому COD = 60°, CD = 8 см. Знайдіть довжину діагоналі.

4. Точка перетину діагоналей прямокутника віддалена від двох його сторін на 3 см і 4 см. Знайдіть периметр прямокутника.

VII. Підсумки уроку

Який з чотирикутників не є прямокутником?

1) Чотирикутник, у якого протилежні сторони паралельні і один кут прямій.

2) Паралелограм, який має прямий кут.

3) Паралелограм, у якого діагоналі рівні.

4) Чотирикутник, у якого діагоналі перпендикулярні і діляться у точках перетину навпіл.

VIII. Домашнє завдання: §4, ст. 30-32, № 148, 149.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок №                                                   Тема. Ромб

 

Дата:

Клас: 8-А, 8-Б

Предмет: геометрія

 

Мета: працювати над засвоєнням учнями змісту означень, власти­востей та ознак ромба. Формувати вміння:

• відтворювати вивчені твердження;
• застосовувати властивості, ознаки ромба до розв'язування типових задач;
• застосовувати властивості, ознаки ромба разом із раніше вивченими твердженнями в темі «Чотирикутники» до розв'язування задач підвищеного рівня складності.

Тип уроку: засвоєння вмінь та навичок.

 

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Перевірку засвоєння учнями теоретичного матеріалу попереднього уроку можна провести або у формі математичного диктанту, або у формі бесіди за тими самими питаннями, що включені в математичний диктант.

Математичний диктант

Варіант 1

1. Чи є прямокутником паралелограм, один із кутів якого прямий?
2. Чи правильно, що кожен прямокутник є паралелограмом?
3. Діагоналі прямокутника АЕКМ перетинаються в точці О. Відрізок АО дорівнює 3 дм. Знайдіть довжину діагоналі ЕМ.
4. Діагоналі чотирикутника рівні. Чи обов'язково цей чотирикутник є прямокутником?

Варіант 2

1. Чи обов'язково чотирикутник з прямим кутом є прямокутником?
2. Чи правильно, що кожен паралелограм є прямокутником?
3. Діагоналі паралелограма мають довжину 3 дм і 5 дм. Чи цей парале­лограм є прямокутником?
4. Сума довжин діагоналей прямокутника дорівнює 13 м. Знайдіть довжину кожної діагоналі.

III. Формулювання мети і завдань уроку

IV. Актуалізація опорних знань та вмінь

З метою свідомого розуміння та подальшого засвоєння змісту означень, властивостей, ознак ромба слід активізувати знан­ня і вміння учнів щодо означення, властивостей та ознак паралелогра­ма, прямокутника; означення, властивостей та ознак рівнобедреного трикутника.

V. Засвоєння знань

План вивчення нового матеріалу

1. Означення ромба.
2. Властивості ромба.
3. Ознаки ромба.

Інша річ, «додаткові» властивості та ознаки ромба.

1. Якщо всі сторони чотирикутника рівні, то цей чотирикутник — ромб.
2. Якщо сусідні сторони паралелограма рівні, то цей паралелограм — ромб.
3. Паралелограм із перпендикулярними діагоналями є ромбом.
4. Якщо діагональ паралелограма є бісектрисою його протилежних кутів, то цей паралелограм — ромб.

Оскільки вони є специфічними (тобто виконуються тільки для ромба), то необхідно їх довести (доведення можна провести за підруч­ником або запропонувати учням виконати його самостійно, або запро­понувати в якості індивідуального завдання для сильних учнів).

	Ромб Означення. Паралелограм, усі сторони якого рівні, називається ромбом
	Властивості	Ознаки
	1. Має всі властивості паралелограма, тобто: 1) А = С, В = D; 2) АО = ОС, ВО = OD	1. Якщо ABCD — чоти­рикутник і AB = BC= CD = AD, то ABCD — ромб
	2. Якщо ABCD — ромб, АС і BD — діагоналі, то: 1) ACBD, 2) OAD = OAB. ODA = ODC	2. Якщо ABCD — пара­лелограм і АВ = ВС, то ABCD — ромб 3. Якщо ABCD — пара­лелограм і AC1BD, то ABCD – ромб 4. Якщо ABCD — пара­лелограм і АС — бісек­триса кутів А і С, то ABCD - ромб

 

VI. Формування первинних умінь

Виконання усних вправ

1. Назвіть види паралелограмів, у яких: а) усі кути рівні; б) усі сторони рівні; в) діагоналі рівні; г) діагоналі перпендикулярні.
2. Діагоналі ромба ABCD перетинаються в точці О. 5). Назвіть: а) бісектрису три­кутника ABD; б) висоту трикутника ABC;

в) медіану трикутника BCD.

3. Діагоналі квадрата ABCD перетинаються в точ­ці О. Назвіть усі рівні трикутники, які утворю­ються при перетині діагоналей. Визначте їх вид.

Виконання графічних вправ

1. Накресліть дві перпендикулярні прямі, які перетинаються в точці О. На одній з прямих відкладіть по різні боки від точки О рівні відрізки ОА і ОС, а на другій прямій — рівні відрізки ОВ і OD. Сполучіть точки A, B, C і D.

а) Виміряйте сторони чотирикутника ABCD і визначте його вид.

б) Виміряйте кут А чотирикутника ABCD. Користуючись власти­востями цього чотирикутника, знайдіть градусні міри інших його кутів. Перевірте результати вимірюванням.

в) Виміряйте кути ADB і CDB. Виділіть кольором усі пари рівних кутів між діагоналями і сторонами чотирикутника.

2. Накресліть прямокутний трикутник ABD з гіпотенузою BD. Про­ведіть через вершини В і D прямі, паралельні сторонам AD і АВ відповідно. Позначте точку С — точку перетину цих прямих.

а) Виміряйте сторони чотирикутника ABCD і визначте його вид.

б) Проведіть діагональ АС. Виміряйте і порівняйте довжини діаго­налей чотирикутника.

в) Позначте на прямих ВС і AD точки С₁ і D₁ так, щоб чотирикутник ABC₁D₁ був квадратом.

Виконання письмових вправ

1. Знайдіть кути ромба, якщо:

а) один із них на 120° більший за інший;

б) одна з його діагоналей дорівнює стороні.

2. Знайдіть кути ромба, якщо кути, утворені його стороною з діагоналями, відносяться як 1 : 4.
3. № 184, 185, 186, 187, 189 (1), 193 (1), 195 (1).

VII. Підсумки уроку

VIII. Домашнє завдання: §5, ст. 37, 38; № 189 (2), 193 (2), 195 (2).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант (закінчи речення)

(на дошці заздалегідь зображено рисунки (ДОДАТОК 1) або слайди демонструються за допомогою проектора)

1. Діагоналі прямокутника… рівні і точкою перетину діляться пополам.
2. Якщо у чотирикутника три кута прямі, то цей чотирикутник – … прямокутник .
3. Прямокутник – це паралелограм, у якого … всі кути прямі.
4.   Якщо у паралелограма один кут прямий, то цей паралелограм – … прямокутник.
5.  У паралелограма протилежні сторони – … паралельні і рівні.
6.  Формула периметра прямокутника має вигляд …

 

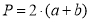
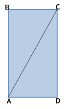
 Задача 1.     Доведіть, що діагональ прямокутника ділить його на два рівні трикутники.

                               Доведення:

 

Розглянемо ∆АВС  і ∆СDА.

  1.∆ АВС і ∆ СDА прямокутні за умовою ( В =  D = 90°),  

   2. ∆АВС = ∆СDА за двома катетами (АВ = СD; ВС = АD).     (або за катетом і гіпотенузою).

 

 

 Задача 2. Доведіть, що кожна сторона прямокутника менша за його діагональ.

Доведення:

 

 Провівши у прямокутнику АВСD діагональ АС утворилося два прямокутних трикутники АВС і   СDА . Так як діагональ лежить проти прямого кута, а (сторони) катети проти гострих кутів, то діагональ завжди більша за катети (проти більшого кута лежить більша сторона).