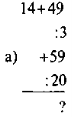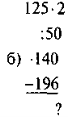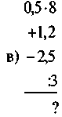Розробка уроку з математики у 6 класі на тему "Взаємно обернені числа"
Тема. Взаємно обернені числа
Мета: ознайомити учнів із поняттям «взаємно обернені числа» і домогтися його засвоєння; виробляти вміння перевіряти чи, є дані два числа взаємно оберненими, знаходити число, обернене до даного.
Тип уроку: засвоєння вмінь та навичок.
Хід уроку
І. Перевірка домашнього завдання
Зібрати зошити, розглянувши (і оцінивши, якщо учні виконали її) додаткову задачу.
ІІ. Актуалізація опорних знань
Усні вправи
- Обчисліть:
|
|
|
|
|
-
Знайдіть такі дроби
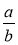 , щоб правильними були рівності:
, щоб правильними були рівності: 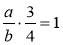 ;
; 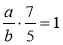 ;
; 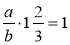 ;
; 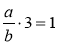 ;
; 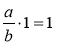 .
.
-
Дано число 10. Знайдіть: а)
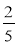 його; б)
його; б) 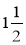 його; в) 20 % його; г) збільште його на 3 %.
його; в) 20 % його; г) збільште його на 3 %.
III. Формування знань учнів
Поняття «взаємно обернені числа» є одним з основних у темі. Тому найголовніше на цьому уроці, незалежно від способу викладання матеріалу, розв'яжіть якомога більше задач, що передбачають закріплення знань про зміст поняття «взаємно обернені числа» та вироблення вмінь знаходити число, обернене до даного.
|
|
Конспект 18 |
|
Взаємно обернені числа |
|
|
тому
тому а і |
Приклади 1) 2) Знайдіть число, обернене до:
а)
Відповідь, а) |
IV. Вироблення вмінь
І рівень
Усні вправи
- Яке число обернене до 1?
-
Назвіть числа, обернені до:
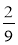 ;
; 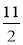 ;
;  ; 2; 0,1.
; 2; 0,1.
- Чи існує число, обернене нулю?
ІІ рівень
Письмові вправи
-
Доведіть, що число 1,6 і 0,625 та числа
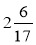 і 0,425 є взаємно оберненим.
і 0,425 є взаємно оберненим.
-
Знайдіть числа, обернені до: 100;
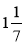 ;
; 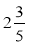 ;
; 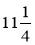 ;
; 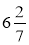 ; 0,6; 0,17; 3,6; 7,35.
; 0,6; 0,17; 3,6; 7,35.
-
Знайдіть значення виразу: а)
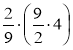 ; б)
; б) 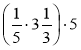 ; в)
; в) 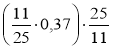 ;
;
г) ![]() ; д) 0,2 · (2,71 · 5); є)
; д) 0,2 · (2,71 · 5); є) 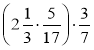 .
.
-
Розв'яжіть рівняння: а)
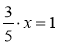 ; б)
; б) 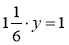 ; в) 0,3 · х = 1; г)
; в) 0,3 · х = 1; г) 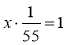 .
.
-
Спростіть вираз: а)
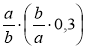 ; б)
; б) 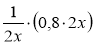 ; в)
; в) 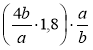 .
.
Додаткові задачі
Задача 1. Добуток трьох чисел дорівнює ![]() . Знайдіть перше з цих чисел, якщо два інших є взаємно оберненими.
. Знайдіть перше з цих чисел, якщо два інших є взаємно оберненими.
Задача 2. Одного разу Петрик Тяпляпкін увесь вечір намагався відшукати два правильних дроби, які були б взаємно оберненими, але все марно. Чому?
Задача 3. Петрик Тяпляпкін записував два будь-які числа, потім знаходив для них взаємно обернені. Потім перемножував усі чотири числа. І, дивна річ, у добутку завжди діставав 1. Чому?
Ігровий момент. Учитель записує на дошці вираз: ![]() і говорить: «Ви можете назвати будь-яке значення х і я одразу ж назву значення всього виразу. Хто може зробити так само?»
і говорить: «Ви можете назвати будь-яке значення х і я одразу ж назву значення всього виразу. Хто може зробити так само?»
V. Підсумки уроку
Повторити основні поняття і способи дій, розглянуті на уроці (взаємно обернені числа, як знайти число, обернене до:
а) звичайного дробу;
б) натурального числа;
в) мішаного числа;
г) десяткового дробу?
Задача. Петрик Тяпляпкін записав у зошит два натуральні числа. Поділив перше на друге — дістав 0,7.
Поділив друге на перше — дістав 0,13. Чи не помилився він?
VI. Домашнє завдання
-
Знайдіть числа, обернені до: 12;
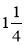 ;
; 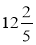 ;
; 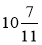 ; 0,3; 0,07; 4,5; 1,23.
; 0,3; 0,07; 4,5; 1,23.
-
Знайдіть значення виразу: а)
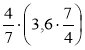 ; б)
; б) 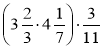 ; в)
; в) 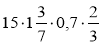 .
.
-
Розв'яжіть рівняння: а)
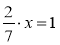 ; б)
; б) 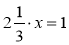 ; в) 0,7 · у = 1; г)
; в) 0,7 · у = 1; г) 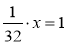 .
.
-
Сума двох взаємно обернених чисел завжди не менша від 2. Перевірте
це, взявши числа: 3 і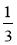 ;
; 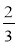 і
і 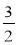 ;
; 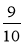 і
і 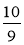 ; 1 і 1.
; 1 і 1.
-
Різниця двох чисел дорівнює 128. Одне з них у 5 разів більше за друге.
Знайдіть ці числа.


про публікацію авторської розробки
Додати розробку