Розробка уроку з презентацією алгебра та початки аналізу 11 клас "Логарифмічна функція"
План – конспект
уроку з алгебри та початків аналізу
урок проводиться в 11–х класах
учитель Чуйко С.В.
Тема уроку: Логарифмічна функція
Мета уроку:
- Розширити знання учнів про логарифмічну функцію, застосування її властивостей в нестандартних ситуаціях.
- Формувати інформаційну компетентність : уміння здобувати, опрацьовувати та використовувати інформацію з різних джерел.
- Вдосконалити уміння учнів перетворювати вирази, що містять логарифми, розв’язувати логарифмічні рівняння і нерівності,
- Формувати навички правильного планування власної діяльності з врахуванням біологічних ритмів, уміння зняти напругу і втому.
Форма проведення уроку: урок-семінар.
Обладнання: логарифмічна лінійка, портрет Дж. Непера, схеми, таблиці.
Підготовка учнів до роботи на уроці.
Учні заздалегідь отримують перелік питань і завдань, які будуть розглядатися на семінарі:
1. Повторити:
а) логарифмічна функція і її властивості;
б) розв‘язання логарифмічних рівнянь та нерівностей
2. Підготувати повідомлення за темами:
а) «Зірки, шум і логарифми»;
б) «Логарифмічна спіраль»;
в) «Логарифми і відчуття»
г) Логарифмічна «комедія: 2>3»;
д) Будь-яке число – трьома двійками;
е ) Логарифмічні чудасії.
Схема проведення уроку-семінару полягає у тому, що учні заслуховують повідомлення, у відповідності з планом підготовки до уроку, розв’язують прикладні задачі на задані теми, беруть участь в обговоренні, підводять підсумки роботи.
Хід уроку
I. Повідомлення теми, мети і завдань уроку
Учитель: «Багато понять курсу алгебри та початків аналізу 10-11 класів носять абстрактний характер, і ми задаємось питанням: «А де ж застосовуються ті знання, які ми отримуємо на уроках математики?». Тема цього семінару не випадкова, ви отримали завдання дізнатися, в яких областях науки, техніки знайшли застосування логарифми, логарифмічна функція. Опрацювавши необхідний матеріал, ви провели велику дослідницьку роботу і виявили, що логарифми, логарифмічна функція має широке застосування у фізиці, хімії, біології, географії, астрономії , а також в економіці банківської справи і виробництва.
– Заповніть колонки таблиці «Застосування логарифмів, логарифмічної функції» (таблиця заздалегідь побудована на дошці)
|
№ з/п |
Предмет |
Застосування логарифмів та логарифмічної функції |
|
1 |
Фізика |
|
|
2 |
Хімія |
|
|
3 |
Біологія |
|
|
4 |
Астрономія |
|
|
5 |
Психологія |
|
|
6 |
Музика |
|
II. Повідомлення учнів за заданими темами, розв‘язування задач:
Учитель: «Ода експоненті».
Потому-то, словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Б.Слуцький
Воістину безмежні застосування показникової і логарифмічної функцій в самих різних галузях науки і техніки, адже логарифми створили для полегшення обчислень. Майже чотири століття минуло з того дня, як у 1614 році були опубліковані перші логарифмічні таблиці, складені Джоном Непером. Вони допомагали астрономам і інженерам, скорочувати час на обчислення, і тим самим, як сказав знаменитий французький вчений Лаплас: “Подовжували життя обчислювачам”.
Ще донедавна важко було уявити інженера без логарифмічної лінійки в кишені. Винайдена через десяток років після появи логарифмів Непера англійським математиком Гунтером вона дозволяла швидко отримувати відповідь, з інженерного ужитку витіснив мікрокалькулятор, але без логарифмічної лінійки не були б побудовані ні перші комп'ютери, ні калькулятори.
Різноманітність застосування показникової (або як ще її називають експоненціальної) функції надихнули англійського поета Ельмера Брілла, він написав «оду експоненті».
Були поети, які не присвячували од експоненті і логарифмам, але згадували їх у своїх віршах. Наприклад, у своєму вірші “Фізики і лірики” поет Борис Слуцький написав ті рядки, які винесені в епіграф до уроку (записані на дошці).
Розпочнемо роботу з прикладів, де логарифми виконують свою безпосередню функцію – полегшення обчислень»
1. Порівняти числа ![]() і
і ![]() .
.
Неважко здогадатись, що використати калькулятор чи комп’ютер для їх порівняння не можна. Оскільки такі числа до них просто «не влізуть». Тому знайдіть десяткові логарифми цих чисел.
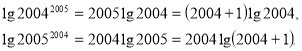
Оскільки 2004 > 3, то можна застосувати нерівність ![]() яка дозволить записати вірну числову рівність
яка дозволить записати вірну числову рівність ![]() , звідки
, звідки ![]() . Оскільки функція
. Оскільки функція ![]() зростаюча, отримаємо:
зростаюча, отримаємо: ![]()
Учитель: «Розв‘язуючи приклад на порівняння чисел, ми говорили про те, що числа ![]() і
і ![]() дуже великі. Цікаво, а як взагалі можна встановити, скільки цифр міститься у десятковому записі числа, представленого подібним чином? Ну, наприклад, скільки цифр міститься у десятковому записі числа
дуже великі. Цікаво, а як взагалі можна встановити, скільки цифр міститься у десятковому записі числа, представленого подібним чином? Ну, наприклад, скільки цифр міститься у десятковому записі числа ![]() ?
?
– Визначити, скільки цифр міститься у десятковому записі числа ![]() ?
?
Спочатку зрозуміємо, що від нас вимагається. Як відомо, запис числа в десятковій системі є порозрядним, тобто нам потрібно знайти число розрядів. А ось тепер найголовніше: число розрядів, наприклад, у чисел 543, 176 ,899 однакове, також воно буде однаковим і у всіх чотиризначних чисел, і у всіх п‘ятизначних і т.д. Значить, можна шукати кількість цифр не в числі ![]() , а в якому-небудь іншому, більш зручному, аби тільки кількість розрядних одиниць співпадала. У даній ситуації найбільш зручним є число – степінь десяти. Адже ці числа завжди розпочинають розрядну групу і до того ж легко записуються:
, а в якому-небудь іншому, більш зручному, аби тільки кількість розрядних одиниць співпадала. У даній ситуації найбільш зручним є число – степінь десяти. Адже ці числа завжди розпочинають розрядну групу і до того ж легко записуються: ![]() .
.
Так, двозначні числа розпочинаються з 10, тризначні з ![]() … Єдине, що нам не подобається , це неспівпадання розряда зі степенем n, адже двозначному числу відповідає n=2 і т.д. Тому замінимо його на число виду
… Єдине, що нам не подобається , це неспівпадання розряда зі степенем n, адже двозначному числу відповідає n=2 і т.д. Тому замінимо його на число виду ![]()
Таким чином, задача зводиться до знаходження найбільшого натурального значення n, при якому вірна нерівність ![]() .
.
– Розв‘яжіть дану нерівність
![]()
Використовуючи калькулятор , отримуємо ![]() Отже, найбільшим натуральним значенням n є число 45, а відповідно число
Отже, найбільшим натуральним значенням n є число 45, а відповідно число ![]() – сорокап‘ятизначне.
– сорокап‘ятизначне.
2. Учитель «А зараз, використовуючи знання основних властивостей логарифмів та логарифмічної функції, розв‘яжемо декілька прикладів та знайдемо помилку в доведенні»
а) Логарифмічна “комедія: 2>3”.
Учень: “Комедія” починається з нерівності ![]() >
>![]() , безперечно правильної. Потім слідує перетворення
, безперечно правильної. Потім слідує перетворення
![]() >
>![]() , теж не викликає сумніву. Більшому числу відповідає більший логарифм, значить:
, теж не викликає сумніву. Більшому числу відповідає більший логарифм, значить:
lg![]() > lg
> lg![]() , 2lg
, 2lg ![]() >3lg
>3lg![]() .
.
Після скорочення на lg![]() маємо 2>3.
маємо 2>3.
– У чому помилка цього доведення?
Розв’язання: Помилка була допущена при скороченні на lg![]() ; оскільки lg
; оскільки lg![]() < 0, то при скороченні на lg
< 0, то при скороченні на lg![]() необхідно було змінити знак нерівності, тобто 2<3. (Якби ми логарифмували не за основою 10, а за іншим додатним числом меншим за 1, то lоgа
необхідно було змінити знак нерівності, тобто 2<3. (Якби ми логарифмували не за основою 10, а за іншим додатним числом меншим за 1, то lоgа![]() > 0, і тоді ми не мали б права стверджувати, що більшому числу відповідає більший логарифм).
> 0, і тоді ми не мали б права стверджувати, що більшому числу відповідає більший логарифм).
б) Будь-яке число – трьома двійками.
Учень : Продовжимо урок дотепною головоломкою алгебри. Пропонується завдання: будь-яке дане число, ціле і додатнє, зобразити за допомогою трьох двійок і математичних символів.
Наприклад: Нехай дане число 3.
Розв’язання:
![]() ,
,
Оскільки . ![]()
![]()
![]()
Аналогічно: 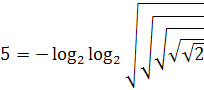 .
.
- записати в загальному вигляді будь-яке ціле додатнє число у вигляді трьох двійок і математичних символів
в)Логарифмічні чудасії.
Розв’яжемо декілька прикладів:
– Обчислити ![]()
![]()
Розв’язанння: Так як ![]() , то
, то ![]() .
.
Висновок: ![]() при 0 < x
при 0 < x![]() , 0 < y
, 0 < y![]() .
.
- Довести, що якщо а і b – довжини катетів,с – довжина гіпотенузи прямокутного трикутника, то:
![]()
Розв‘язання: приведемо всі логарифми до основи b+c:
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Повторюючи логарифмічні викладки у зворотному порядку, доведемо вихідну рівність. Потім, що вона вірна при додаткових обмеженнях ![]() ,
, ![]() .
.
3. Повідомлення учня:
«Зірки, шум і логарифми»
Цей заголовок зв'язує настільки, здавалося б, несумісні речі. Шум і зірки об'єднуються тут тому, що гучність шуму і яскравість зірок оцінюється однаковим чином – за логарифмічною шкалою.
Астрономи ділять зірки за ступенем яскравості на видимі і абсолютні зоряні величини – зірки першої величини, другої, третьої і так далі. Послідовність видимих зоряних величин, що сприймаються оком, є арифметичною прогресією. Але фізична сутність виражається за іншим законом: яскравості зірок складають геометричну прогресію із знаменником 2,5. Легко зрозуміти, що “величина” зірки є логарифмом її фізичної яскравості. Коротше кажучи, оцінюючи яскравість зірок, астроном оперує таблицею логарифмів, складеною за основою 2,5.
Аналогічно оцінюється і гучність шуму. Шкідливий вплив промислових шумів на здоров'я працівників і на продуктивність їхньої праці спонукало виробити прийоми точної числової оцінки гучності шуму. Одиницею гучності звуку служить “бел”, але практично використовується одиниця гучності, рівна його десятій долі, - так званий “децибел”. Послідовні міри гучності 1 бел, 2 бели, 3 бели, і так далі складають арифметичну прогресію. Фізичні ж величини, що характеризують шуми (енергія, інтенсивність звуку і ін.), складають геометричну прогресію із знаменником 10. Гучність, виражена в белах, дорівнює десятковому логарифму відповідної фізичної величини.
– Збільшення діаметра об‘єктива телескопу дозволяє бачити усе більшу кількість зірок, невидимих неозброєним оком. При цьому максимальна «зіркова величина» k зірки, видимої через телескоп, наближено обчислюється за формулою
k = 7,5 + ![]() , де D – діаметр об‘єктива телескопа в сантиметрах. Наприклад, при D = 8 см k = 7,5 +
, де D – діаметр об‘єктива телескопа в сантиметрах. Наприклад, при D = 8 см k = 7,5 + ![]()
![]() 12. Отже, через телескоп можна побачити зірки до 12-ї величини.
12. Отже, через телескоп можна побачити зірки до 12-ї величини.
– Обчислити k, якщо D = 16 см.
Підставимо дане значення діаметра у формулу. Отримаємо:
k = 7,5 + ![]()
![]() 13,5.
13,5.
Відповідь: ![]() .
.
4. Повідомлення учня: “Логарифми і відчуття”.
Відчуття, що сприймаються органами чуття людини, можуть викликатися роздратуваннями, що відрізняються один від одного в багато мільйонів і навіть мільярдів разів. Удари молота об слизьку плиту в сто разів голосніші, ніж тихий шелест листя, а яскравість дуги вольта в трильйони разів перевищує яскравість якої-небудь слабкої зірки, ледве видимої на нічному небосхилі. Але жодні фізіологічні процеси не дозволяють дати такого діапазону відчуттів. Досліди показали, що організм як би “логарифмує” отримані ним роздратування, тобто величина відчуття наближено пропорційна десятковому логарифму величини роздратування.
Як бачимо, логарифми проникли і в область психології.
5. Повідомлення учня «Логарифмічна спіраль».
Літак, що вилетів з якої-небудь точки земної кулі на північ, через деякий час виявиться над Північним полюсом. Якщо ж він полетить на схід, то, облетівши паралель, повернеться в той же пункт, з якого вилетів. Передбачимо тепер, що літак летітиме перетинаючи всі меридіани під одним і тим же кутом, відмінним від прямого, тобто тримаючись весь час одного і того ж курсу. Коли він облетить земну кулю, то потрапляє в точку, що має ту ж довготу, що і точка вильоту, але розташовану ближче до Північного полюса. Після наступного обльоту він виявиться ще ближчим до полюса і, продовжуючи летіти вказаним чином, описуватиме довкола полюса спіраль, що звужується.
Рівняння цієї спіралі:
r = aek? ,
де r – відстань від довільної точки М на спіралі до вибраної точки О, ? – кут між променем ОМ і вибраним променем Ох , a і k – постійні.
Розв’язуючи його, отримаємо:
ln ek? = ln ![]() , k? = ln
, k? = ln ![]() , ? =
, ? = ![]() ln
ln ![]() .
.
Оскільки це рівняння пов'язане з логарифмічною функцією, то обчислену за цією формулою спіраль називають логарифмічною.
Живі істоти зазвичай виростаючи, зберігають загальний контур своєї форми. При цьому вони зростають у всіх напрямках – доросла істота і вища і товща за дитинча. Але раковини морських тварин можуть зростати лише в одному напрямі. Аби не дуже витягуватися в довжину, їм доводиться скручуватися, причому кожен наступний виток подібний до попереднього. А таке зростання може здійснювати лише по логарифмічній спіралі або її деяким просторовим аналогам. Тому раковини багатьох молюсків, равликів, а також роги таких ссавців, як архари (гірський козел), закручені по логарифмічній спіралі. Можна сказати, що ця спіраль є математичним символом співвідношення форм зростання. Великий німецький поет Йоганн Вольфганг Гете вважав її навіть математичним символом життя і духовного розвитку.
Контури, виражені логарифмічною спіраллю, мають не лише раковини в нитці довкола центру по логарифмічній спіралі. По логарифмічних спіралях закручено і багато галактик, зокрема, Галактика, якій належить Сонячна система.
6. Логарифми в електроосвітленні.
Учитель: «Причиною того, що наповнені газом лампочки дають більш яскраве світло, ніж не заповнені газом, з металевою ниткою розжарювання з того ж матеріалу, криється в різній температурі розжарювання. За правилом, установленому в фізиці, загальна кількість світла, що випромінюється при накалюванні, зростає пропорційно 12 степеню абсолютної температури. Знаючи це, визначіть у скільки разів лампа, температура нитки розжарювання якої 2.5000 абсолютної шкали, випромінює більше світла, ніж пустотна розжарена до 2.2000.»
Розв‘язання.
![]()
![]() Позначимо шукане відношення через Х, маємо рівняння:
Позначимо шукане відношення через Х, маємо рівняння:
![]()
![]() 2 5000 12 25 12
2 5000 12 25 12
Х = 2 2000 = 22 , звідки: lgx=12(lg25 – lg22); х=4,6
Розжарена газом лампа випромінює світла в 4,6 разів більше, ніж пустотна.
7. Логарифми у хімії
– Розв‘яжіть задачу.
На скільки градусів потрібно підвищити температуру для пришвидшення хімічної реакції в 59000 разів, якщо швидкість реакції зростає в геометричній прогресії із знаменником 3 при підвищенні температури на кожні 10°?
Розв‘язання.
3x=59000; lg 3x = lg 59000; x lg3 = 59000;
![]()
10° · x = 100°
Відповідь: потрібно підвищити температуру на 100° для пришвидшення хімічної реакції в 59000 разів.
ІІІ. Підсумок уроку
Учитель : «Ще раз звернемось до таблиці, яку ми заповнювали протягом уроку і назвемо , в яких областях науки і техніки мають застосування логарифми і логарифмічна функція.
На завершення роботи можна сказати, що ми , звичайно, не вичерпали всіх прикладів застосування логарифмів, але ті задачі, що ми розв’язали на цьому уроці дали нам розуміння того, яка широка сфера застосування логарифмів. Логарифми знаходять широке застосування при обробці результатів тестування в психології і соціології, при складанні прогнозу погоди і ,навіть, в музиці , а також в інших областях науки і техніки.
Сподіваюсь, що отримані на уроці знання і вміння , додаткова освітня інформація дозволить у майбутньому плідно використати її в життєвих ситуаціях».
Домашнє завдання
1. Зробіть розрахунок: яке підвищення абсолютної температури ( у %) необхідно для подвоєння яскравості лампочки?
Розв‘язання. Складемо рівняння :
(1+![]() ) = 2, звідки: lg (1+
) = 2, звідки: lg (1+![]() ) =
) = ![]() і x = 6 %.
і x = 6 %.
2. Чисельність популяції деякого виду тварин складає 5 тисяч. За останній час з різних причин ( браконьєрство, скорочення ареалу проживання ) вона щорічно скорочувалася на 8%. Через скільки років (якщо не будуть вжиті заходи з врятування даного виду і збережуться темпи його скорочення) чисельність тварин досягне межі – 2 тис. , за яким розпочнеться вимирання цього виду? ( при розв‘язанні використати формулу складних відсотків 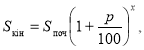
Розв‘язання. Застосуємо для обчислення часу формулу складних відсотків 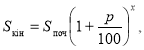
![]() 2 тис. тварин ;
2 тис. тварин ;
![]() 5 тисяч тварин;
5 тисяч тварин;
p = 8 - % скорочення чисельності тварин.
Попередньо розділивши обидві частини рівняння на 1000, отримаємо:
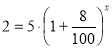
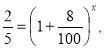
![]()
![]() років.
років.
3. Завдання творчого характеру
Підготувати повідомлення : «Логарифми і музика»

про публікацію авторської розробки
Додати розробку
