Розв'язання системи рівнянь та нерівностей з параметрами.

При яких значеннях параметра а  має розв’язки  система :

         ?

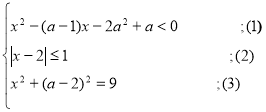Розв’язок.

Побудуємо графік нерівностей (1) і (2) та рівняння (3) в системі хоа. Знайдемо множину точок координатної площини, координати яких є розв’язками даної системи.

Знайдемо корені тричлена в лівій частині нерівності  (1)

х₁=2а-1; х₂=-а.

Прямі,задані рівнянням   х=2а-1 та х=-а ( а=0.5х+0.5;   а=-х)

розбивають координатну площину хоа на чотири області, в кожній з яких квадратний тричлен

зберігає постійний знак.

Розв’язком нерівності будуть виділені області площини.

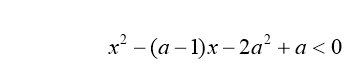
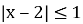2. Ця нерівність задає множину точок координатної площини хоа, розташованих між прямими х=-1 та х=1.

визначає такі області координатної площини:

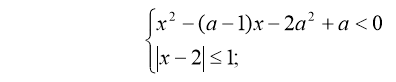
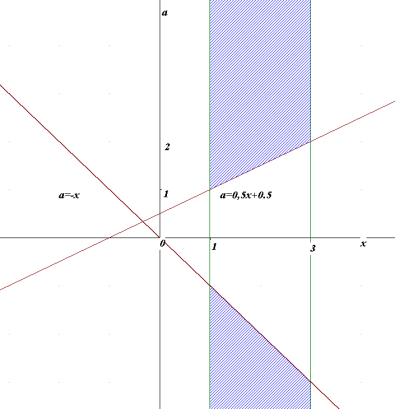
3. х²+(а-2)²=9 це рівняння кола з центром в точці (0;2) та R=3.

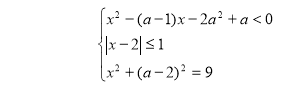
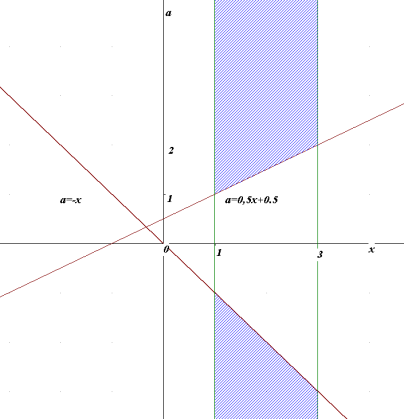
Знайдемо координати точки А(х;а) з системи:   ; А(1;2+.

Точки   В(х;а): 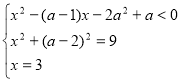;   В(3;2).

Точка  С(1;-1) не належить колу   х²+(а-2)²=9:     1²+(-1-2)²9.

Аналізуючи отриманий графік даної системи, робимо висновок, що її розв’язками є абсциси точок площини, які належать дузі АВ  кола (3).

Отже система має розв’язки при а Є.

Відповідь: система має розв’язки при  а Є.