Розв'язок графічних параметрів на НМТ.
Питання 1. При яких значеннях параметра a рівняння |x2 − 2x − 3| = a має рівно три корені?
Розв’язок:
Для початку розпишемо |x2 −2x−3| =2a , як дві функції y = |x2 −2x−3| і y = a. Тобто, нам потрібно побудувати y = |x − 2x − 3|, щоб дізнатися, чому може дорівнювати a, щоб було рівно три корені.
Почнемо побудову з квадратичної функції y = x2 − 2x − 3.
Щоб побудувати квадратичну функцію y = ax2 + bx + c, необхідно знати:
• Напрям віток параболи: чи вона прямує вгору або вниз: (a > 0,a < 0).
• Перетин з Oy: (c).
• Координати вершини параболи:![]() .
.
У нашому випадку![]() .
.
Починаємо малювати рисунок, тобто будуємо параболу, в якій напрям віток вгору, перетин з Oy в точці −3 і початок параболи в точці (1,−4).
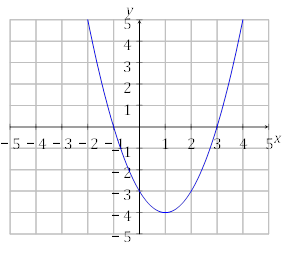
Рис. 1: Графік функції y = x2 − 2x − 3.
Тепер час будувати y = |x2 − 2x − 3|, щоб побудувати графік функції y = |f(x)|, частину графіка y = f(x), що лежить над віссю OX, зберігаємо, а частина його, що лежить під віссю OX, відбивається симетрично щодо осі OX.
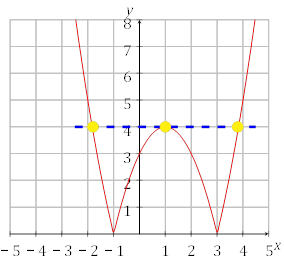
Рис. 2: Графік функції y = |x2 − 2x − 3| та пряма y = 4.
Час будувати пряму y = a, дивлячись на графік ми будемо мати рівно три корені тільки коли y = 4. Отже ми маємо рівно три корені, коли a = 4. Відповідь: a = 4.
Питання 2. При яких значеннях параметра a рівняння |x2 − |x|| = a має чотири корені?

Розв’язок:
Для початку розпишемо |x2 − |x|| = a , як дві функції2 y = |x2 − |x|| і y = a. Тобто, нам потрібно побудувати y = |x − |x||, щоб дізнатися, чому може дорівнювати a, щоб було рівно чотири корені.
Для початку побудуємо графік функції y = x22− x, потім за допомогою2 перетворень цього графіка, враховуючи, що2 2 x = |x| , отримаємо графік функції y = ||x| − |x|| = |x − |x||. 2
Щоб побудувати квадратичну функцію y = ax + bx + c, необхідно знати:
• Напрям віток параболи: чи вона прямує вгору або вниз: (a > 0,a < 0).
• Перетин з Oy: (c).
• Координати вершини параболи:![]() .
.
У нашому випадку![]() .
.
Починаємо малювати рисунок, тобто будуємо параболу, в якій напрям віток вгору, перетин з Oy в точці 0 і початок параболи в точці (0,5;−0,25).
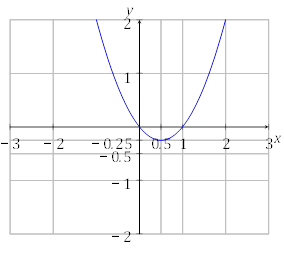
Рис. 3: Графік параболи y = x2 − x.
Тепер побудуємо графік функції y = x2 − |x|.
Графік функції y = f(|x|) маємо із графіка функції y = f(x) у такий спосіб: при x≥0 графік y = f(x) зберігається, а при x < 0 дана частина видаляється і частина, де x≥0 відбивається симетрично відносно осі Oy.
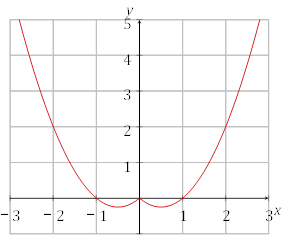
−1
Рис. 4: Графік функції y = x2 − |x|
Залишилось побудувати y = |x2 − |x||, щоб побудувати графік функції y = |f(x)|, частину графіка y = f(x), що лежить над віссю OX, зберігаємо, а частина його, що лежить під віссю OX, відбивається симетрично щодо осі OX.
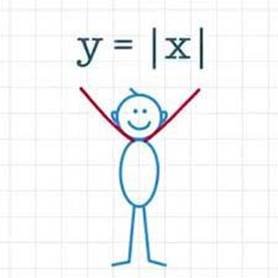
y y 5 5
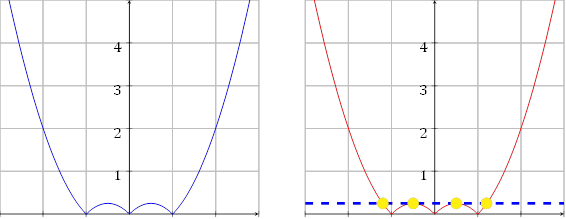
−3 −2 −1 1 2 3x −3 −2 −1 1 2 3x
Рис. 5: Графік функції y = |x2 − |x|| Рис. 6: Графік функції y = |x2 − |x|| та пряма y = 0.25
Час будувати пряму y = a, дивлячись на графік ми будемо мати рівно чотири корені тільки коли y = 0.25. Отже ми маємо рівно чотири корені, коли a = 0.25. Відповідь: a = 0.25.
Питання 3. При яких значеннях параметра a рівняння |x + 1| − |x − a| = 3 має безліч коренів?
Давайте проведемо деякі перетворення та визначимо дві окремі функції:
• Перетворили рівняння: |x + 1| − 3 = |x − a|.
• Розглянемо функцію: y = |x + 1| − 3.
• Розглянемо функцію: y = |x − a|.
Спочатку розглянемо функцію y = |x + 1| − 3. Потім ми побудуємо графік для функції y = |x − a|. Аналізуючи ці графіки, ми знайдемо відповідь.
• Будуємо графік y = x. Починаємо з побудови графіка простої функції y = x. Це лінія, яка проходить через всі точки з координатами (x,y).
• Виконуємо перетворення та будуємо y = x+1. Застосовуючи перетворення до оригінальної функції y = x, додаємо одиницю до значень x, щоб отримати нову функцію y = x + 1. Це зміщує графік вгору на одиницю вздовж вісі y.
• Використовуємо модульне перетворення та будуємо y = |x+1|. Застосовуючи модульне перетворення до функції y = x + 1, ми використовуємо модуль для забезпечення того, щоб графік був позитивний у всіх точках. Це означає, що будь-які від’ємні значення x + 1 будуть перетворені у від’ємні значення y.
• Знову виконуємо перетворення та будуємо y = |x + 1| − 3. Знову застосовуючи перетворення до функції y = |x + 1|, ми віднімаємо три від кожного значення y, щоб отримати нову функцію y = |x + 1| − 3. Це зміщує графік вниз на три одиниці вздовж вісі y.
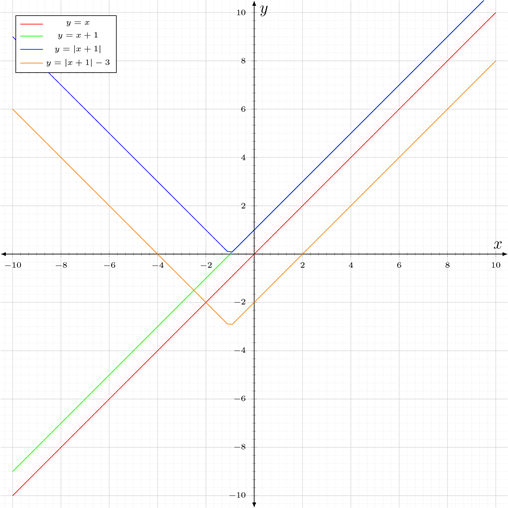
Якщо почати будувати функцію y = |x − a|, то ця функція може зсуватися вліво або вправо в залежності від значення параметра a. Наприклад:
• Якщо a = 0, то графік не має коренів, оскільки абсолютне значення від будь-якого числа буде завжди додатнім.
• Якщо a = −4 або a = 2, то функція матиме безліч коренів, оскільки в цих випадках графік буде перетинатися з віссю x у декількох точках.
• Якщо a = −4.5 або a = 2.5, то функція матиме один корінь, оскільки графік буде торкатися вісі x в одній точці.
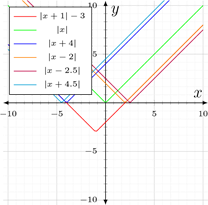
Отже, щоб дане рівняння мало безліч коренів, потрібно, щоб a = −4 або a = 2.
Відповідь: a = −4, a = 2.
Питання 4. При яких значеннях параметра a рівняння |x − 2| = a має рівно один корінь?
Для початку розпишемо |x − 2| = a як систему рівнянь y = |x − 2| і y = a. Тепер потрібно побудувати графік функції y = |x − 2| та пряму y = a і подивитися, де вони перетинаються. І обрати перетин, де рівняння |x − 2| = a має один корінь.
Спочатку розглянемо функцію y = |x − 2|. Потім ми побудуємо графік для функції y = a. Аналізуючи ці графіки, ми знайдемо відповідь.
• Виконуємо перетворення та будуємо y = |x−2|. Застосовуючи перетворення до оригінальної функції y = |x|, віднімаємо 2 від значень x, щоб отримати нову функцію y = |x − 2|. Це зміщує графік вправо на дві одиниці вздовж вісі x.
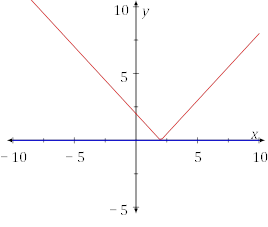
![]()
Отже, щоб дане рівняння мало один корінь, потрібно, щоб a = 0.
Відповідь: a = 0.


про публікацію авторської розробки
Додати розробку
