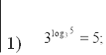Тема уроку: «Логарифми та їх властивості»

 Навчальні цілі заняття:

Знати:

1Означення логарифма

2Властивості логарифмів

3Використання логарифмів при моделюванні реальних процесів і явищ Вміти:

1Обчислювати логарифми.

2Знаходити невідоме за його логарифмом.

3Логарифмувати та потенціювати вирази.

4Застосовувати логарифм для опису реальних процесів.

Виховні цілі:

1Формувати навички раціонального використання кожної робочої хвилини.

2Розвивати математичну мову студентів, кмітливість, увагу, логічне мислення.

3 Сприяти розвитку інтересу до математики.

4Процес логарифмування і потенціювання сприяє розвитку таких розумових операцій, як аналіз, узагальнення, підвищує математичну культуру студентів.

5 Виховувати спостережливість, акуратність,точність виконання дій, розуміння значимості алгебри серед інших наук.

 

Тип уроку: засвоєння нових знань і вмінь.

 

Структурно-логічна схема взаємозв’язків основних понять і способів діяльності які розглядаються в темі:  «Логарифми»

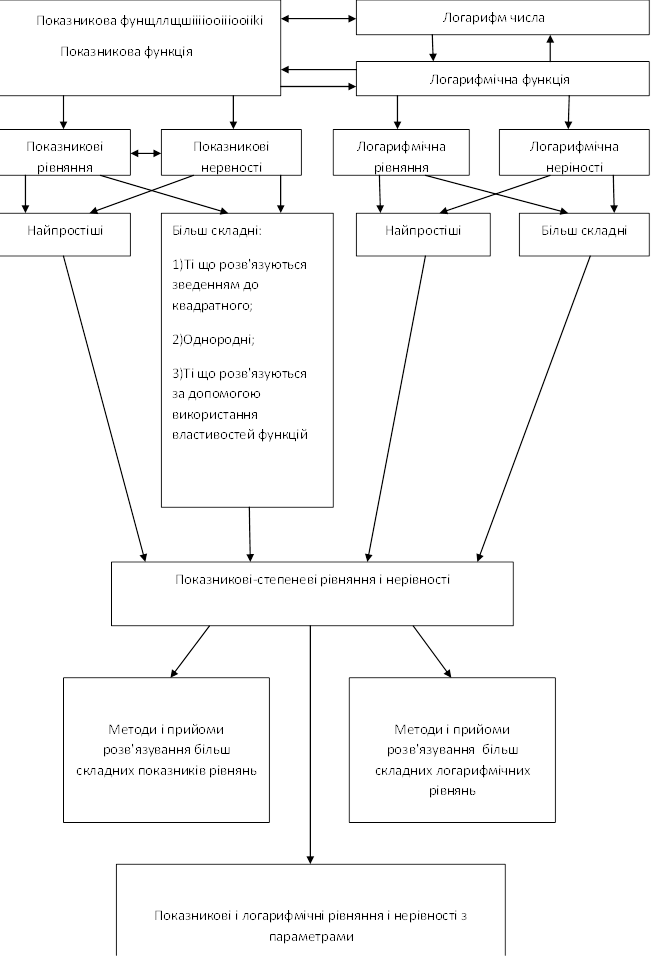
 І. Підготовчий етап

1.     Організаційна частина.

   Формування мети і завдань уроку.

2.     Мотивація навчальної діяльності.

Математика – це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково – технічний прогрес. Одним із понять математики, яке розкриває красу природи, її загадки, досягнення науки і техніки, мистецтва є логарифмічна функція.

 

3.     Інформація для здобувачів освіти :

-         Орієнтовний план вивчення теми;

-         Кількість навчальних годин;

-         Приблизний зміст матеріалу;

-         Основні вимоги до знань і вмінь здобувачів освіти;

-         Терміни проведення контрольної роботи;

-         Орієнтовний зміст завдань, що будуть внесені на контрольну роботу.

4. Актуалізація опорних знань.

 

Почнемо із завдання на увагу

Прочитайте вислів М.Амосова: «У більшості хвороб винна не природа, не суспільство, а сама людина. Найчастіше вона хворіє через лінощі й жадобу. Щоб бути здоровим, потрібні власні зусилля, постійні й значні».

Полічіть частоту використання у цьому вислові літери «і».

Виконання усних вправ («вільний мікрофон»)

1)   Подайте у вигляді степеня з основою 2:

4; 32; 128; ;; 2;³ 4;⁵ 8; ¹ ; ¹ ;1. 2 ³ 16

                                                                                                1         2        3           1

Відповідь:2²;2⁵;2⁷ ;2^1;2^2;2² ;2³ ;2⁵ ;2^2 ;2^;2⁰.

4

2)   Обчисліть: 2⁶;3⁴;^_^1_ ;16^ ; 11⁴; 7^2;0,4³;0,1^3. 5

Відповідь:64;81;625;;121;;0,064;1000.

3)   До якого степеня потрібно піднести : а) число 2, щоб дістати 8; б) число  , щоб дістати ; в) число 1000, щоб дістати 0,1; г) число 3, щоб дістати .

д) число 7, щоб дістати 49; е) число 32, щоб дістати 2?

Відповідь:a)3;б)2;в);г)-2;д)4;е).

ІІ. Основний етап

1. Вивчення нового матеріалу.

                 План вивчення нового матеріалу:

Відеоурок «Логарифми та їх властивості»

     1.Означення логарифма

     2.Десятковий та натуральний логарифм

3.   Властивості логарифмів

4.   Формула переходу до іншої основи

Презентація «Застосування логарифма»

Відеоуроки «Розв’язання вправ»

Відеоуроки «Підготовка до ЗНО» (посилання в дистанційному курсі - тема 1)

 

        

                            Слово вчителя 

А зараз повернімось до теми сьогоднішнього уроку: «Логарифм числа та його властивості». Я сподіваюся, що цей урок пройде цікаво, з великою користю для всіх. Дуже хочу, щоб ті, хто ще байдужий до цариці всіх наук, з нашого уроку пішов із глибоким переконанням: Математика - цікавий і дуже потрібний предмет.

Алгебру називають теорією розв’язування рівнянь. На сьогоднішньому уроці  ми  введемо нове поняття – логарифм числа, яке допоможе розв’язувати задачі, що передбачають використання властивостей логарифмів. 

Для успішного розв’язування вправ на уроці ми повинні знати:

•      Означення логарифма числа.

•      Означення десяткового і натурального логарифма.

•      Основну логарифмічну тотожність.

•      Властивості логарифмів.

 

 Розглянемо рівняння a^х  N , де а і N – деякі числа, причому a 0і a 1 . Якщо N  0, то це рівняння не має коренів, бо значення показникової функції ya^хдодатні при будь-якому х.

 Для N  0 рівняння має корінь, і до того ж єдиний. Справді, областю значень показникової функції ya^хпри a 1є множина додатних чисел. Крім того, кожне своє значення показникова функція набуває лише при одному значенні аргументу( отже, цей корінь єдиний).

Означення: Логарифмом числа N за основою a ( a 0;a1)

називається показник степеня х, до якого треба піднести a , щоб дістати число N .

 

Наприклад:  

1)    5³ 125  log₅125  3;

2)    6^2   log₆ ¹ 2;

36

3)    7⁰ 1 log₇1 0.

 Слово «логарифм» у математичних записах замінюють символом log . Запис log_a N  хозначає, що а^х  N . Запис log₂16читають так: логарифм числа 16 зо основою 2.

 Вирази log₂ 0та log₂16не мають смислу, бо рівняння 2^х 16і 2^х  0 не мають розв’язків.

Вираз log_a N , де a 0і a 1, має смисл лише при N  0.

Логарифмічна рівність     log_a N  bі показниковa рівність a^b  Nвиражають одне й те саме співвідношення між числами a,b, N . 

За цими рівностями можна знайти одне з трьох чисел, що входять до них, якщо задано два інші.

Відповідно до цього можна розв’язати три задачі:

1)  Знайти число N за даним його логарифмом b і його оновою а.

2)  Знайти основу а за даним числом N і його логарифмом b.

3)  Знайти логарифм b даного числа N за даною основою а. 

 У математиці широко використовують десяткові логарифми, це логарифми за основою 10. Для запису таких логарифмів застосовують символ lg ,замість log₁₀ Nпишуть lg N .

                     Наприклад:  1) lg100  2 ;

2)   lg1000  3; 

3)   lg0,01 2.

 Натуральні логарифми. В математичних дослідженнях використовують логарифми за основою, вираженою ірраціональним числом, наближене значення якого дорівнює 2,718281828459045…або ≈ 2,718. Леонард Ейлер запропонував позначити це число літерою е. Його називають неперовим числом на честь шотландського математика Джона Непера(15501617).

 Логарифми з основою е називають натуральними, або неперовими, і позначають ln х . Тут основу е не пишуть, а лише мають на увазі. Отже,

ln х log_e х

 

                       Наприклад: 1) ln e1;

2)    ln1 _ 0;

3)    ln 2  0,693.

 Натуральний логарифм приблизно в 2,3 рази більший за десятковий логарифм того самого числа.

 

Основна логарифмічна тотожність. Розглянемо показникову рівність 

                                                           a^х _ N.                                                (1)

За означенням логарифма,

                                                       х  log_a N.                                               (2)

Підставимо цей вираз у показникову рівність (1). Дістанемо:

                                        

alog_a N N

                                                              

Ця рівність називається основна логарифмічна тотожність. Вона є коротким записом означення логарифма.

Наприклад: 1) 5^log5125 125;                 2) 10^lg1000 1000;

log₁ 9

                                                3) ^_^1_ ³ _ 9.

3

Приклад 1. Записати у вигляді логарифмічних рівностей:

                                                    а) 2⁷ 128;            б) 5^3 _ ¹ ;      в) 216 6. 125

Розв’язання. Застосовуючи означення логарифма даного числа за даною основою, маємо:

а) log₂128  7;         б) log₅ ¹ 3;       в) log₂₁₆ 6  . 125

Приклад 2. За означенням логарифма, визначити, яке число має логарифм 3 за основою 7.

Розв’язання.За умовою log₇ х  3,звідси х 7³  343.

Приклад 3. Знайти основу х, якщо log_х ¹ 2.

49

                     Розв’язання. Маємо: х^2  49^{1 ,} х¹₂  ₄₉¹ ;х²  49;х 7.

            Приклад 4. Знайти логарифм числа  за основою     3.

                       Розв’язання. Маємо: log _{3 9}1 х^; ³^х  ¹₉;3^2х  3^2;х4.

Операцію знаходження логарифмів чисел називають логарифмуванням. Операція логарифмування обернена операції піднесення до степеня при фіксованій основі. 

                    Широкі застосування логарифмів ґрунтуються на їхніх властивостях.

Проблема:А чи можна без таблиці логарифмів швидко і точно обчислити значення виразів :  log₃ 54 - log₃ 6;         log₆ 3 + log₆ 2?

    

Основні властивості логарифмів

 Властивості виражаються в ряді теорем, на яких ґрунтується практичне застосування логарифмів.

Теорема 1. Логарифм добутку двох додатних чисел дорівнює сумі  логарифмів цих чисел, тобто

log_aх у  log_a х  log_a у, де х 0, y 0.

Доведення. Візьмемо два додатні числа х і у у вигляді степеня з основою а (a 0;a 1). За основною логарифмічною тотожністю, маємо:

х_аlog_a ^х і у_аlog^{a y} .

 Знайдемо добуток цих чисел за правилом множення степенів з однаковими основами й запишемо результат за означенням логарифма:

                      х у  аlog_a х аlog_a y;х у  аlog_a хlog_a y.

Маємо: log_aх у  log_a х  log_a у,х  0, y  0,a  0,a 1

Аналогічно можна довести й інші властивості логарифмів для чисел

х 0, y 0,a 0,a1..

Теорема 2. Логарифм частки двох додатних чисел дорівнює різниці  логарифмів цих чисел, тобто

 logaху loga х loga y. 

Теорема 3. Логарифм степеня додатного числа дорівнює показнику степеня, помноженому на логарифм основи цього степеня, тобто

log_a х^т mlog_a х

Теорема 4. Логарифм кореня з додатного числа дорівнює логарифму підкореневого виразу, поділеному на показник кореня, тобто

1 loga n х  loga х n

Теорема 5. Якщо логарифми двох додатних чисел за тією самою основою рівні, то й самі числа рівні. І навпаки, якщо два додатні числа рівні, то і їх логарифми за тією самою основою рівні, тобто

log_a b  log_a c  b  c,a  0,a 1,b  0,c  0.

До основних властивостей логарифмів належать ще й такі.

6.    log_a1 0

7.    log_a a1

Основні властивості логарифмів широко використовуються під час перетворення виразів, що містять логарифми. Окремим видом таких перетворень є логарифмування виразів.

    

Прологарифмуватиодночлен означає виразити його логарифм через логарифми додатних чисел (позначених цифрами і літерами), що входять до його складу.

 Користуючись теоремами про логарифм добутку, частки, степеня і кореня, можна прологарифмувати будь-який одночлен. Під час логарифмування основою будемо вважати число 10.

Приклад 5. Прологарифмувати вирази:

 а)х 5ас(а 0,c 0);       б)х 11а²b³ (a  0,b  0).

Розв’язання. а) даний вираз є добутком, а тому, за теоремою 1:

lg х lg5  lg a lgc.

б) за теоремами 1 і 3: lg х lg11 2lga 3lgb.

    

Потенціювання. Перетворення, за допомогою якого за даним логарифмом числа (виразу) визначають саме число (вираз), називають потенціюванням. Це перетворення є оберненим до логарифмування.

 

Приклад 6. Пропотенціювати вираз, тобто знайти х за його логарифмом.

                       lg х 7lgb 2lgc(b 0;c 0).

Розв’язання.Скористаємося теоремами 3 і 2:

lg х lgb⁷ lgc²,lg х lg bc₂7 ;хbc27 .

Формула переходу від однієї основи логарифма до іншої

(a 0,a1,b 0,b1, х 0) :

log loga х b х logb a

log²10; Наприклад: 1) log₅10  log₂ 5

2)    log₅10 _ ^log310;  log₃ 5

3)    log₅10 _ ^loga10. log_a 5

 

Деякі важливі тотожності, що містять логарифми

1 logb a    ; (a 0,a1,b 0,b1) loga b

1) 

2) log_a b ^log_ak b^k;(a 0,a1,b 0)

logan bm  mn loga b;(a 0,a1).

3) 

Наприклад: 

1)   Спростити вираз log ₂₅ 36.

                      Розв’язання: log₂₅ 36  log₅2 6²  log₅ 6.

2)   Знайти значення виразу log₈ 4.

                    Розв’язання: log₈ 4  log₂3 2²  ²₃.

3)   Подати log₃ 7у вигляді логарифма з основою 7.

                    Розв’язання: log₃ 7  ¹ .

log₇ 3

 

 

Опорний конспект

 

1. Логарифм числа
Означення					Приклади
Логарифмом додатного числа b (b > 0) за основою а (а >0, a ≠1) називається показник с, до якого треба піднести а,  щоб одержати b. Позначення: loga b;    loga b=с, ас =b Дія знаходження логарифма – логарифмування.					1.                log4 16 = 2, оскільки 42 = 16 2.                log7          , оскільки
Десятковий логарифм – це логарифм за основою 10. Позначення: log10b = lg b					lg 1000 = 3, оскільки                                  103 = 1000
Натуральний логарифм – це логарифм за основою е (е ≈ 2,7182818). Позначення: logеb = ln b					ln =-2, оскільки е-2 = .
2. Основна логарифмічна тотожність
, а > 0, a ≠ 1, b > 0                                   2)
3. Властивості логарифмів і формули логарифмування
1) loga 1 = 0,  а > 0, a ≠ 1		Логарифм одиниці за будь-якою основою дорівнює нулю.				log7 1 = 0  , 70 = 1
2) loga а = 1, а > 0, a ≠ 1		Логарифм будь-якого числа за такою ж  основою дорівнює одиниці.				log8 8 = 1, 81 = 8
3.       loga (ху)= loga х + loga у  (а > 0, a ≠ 1,  x > 0, y > 0)		Логарифм добутку додатних чисел дорівнює сумі логарифмів множників.				log3 2 + log3 4,5 = log3 (2·4,5)= = log39 = 2, 32 = 9
4)  , (а > 0, a ≠ 1,  x > 0, y > 0)		Логарифм частки при діленні  додатних чисел дорівнює різниці логарифмів діленого і дільника.
5) , (а > 0, a ≠ 1,  x > 0)		Логарифм степені додатного числа дорівнює добутку показника степеню на логарифм основи.
4. Формула переходу до іншої основи
,  a, b, c – додатні, a ≠ 1, c ≠1			1)         2)
	Наслідки
(а > 0, a ≠ 1,  b > 0, b ≠ 1)	(а > 0, a ≠ 1,  b > 0)			(а > 0, a ≠ 1,  b > 0)			(а > 0, a ≠ 1)

 

 

2. Осмислення нового матеріалу.

Параграф 4 на стор. 32 – 38.  (Істер О. Математика 11 клас 2019р.) 

№ 4.8,  4.16,  4.31, 4.48 (парні приклади).

 

 

 

 

 

 

Гра «Влучні стрільці».

 

Гра «Вставляйка»

       

                                    

ІІІ. Заключний етап

 

Самостійна робота

 

 

                                                                                                                

    

 

 

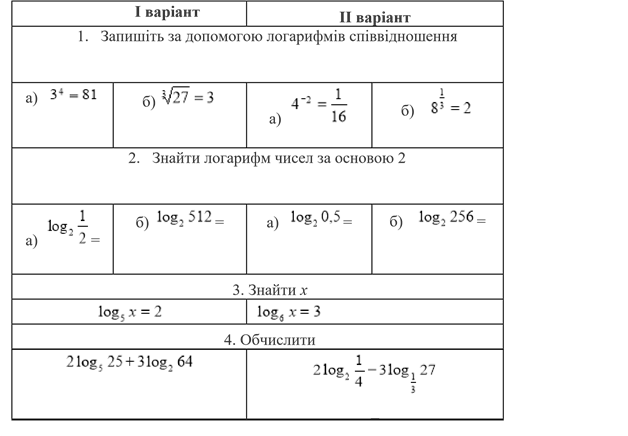
Завдання на повторення шкільного курсу математики

Задача 1

 

Відстань від Бердичева до Солотвина 22 км. Автобус подолав цю відстань за 25 хв. З якою швидкістю рухався автобус? Розв’язання.

Щоб знайти швидкість, треба відстань поділити на час. Залежність між швидкістю V, відстанню S і часом руху t у математиці виражають формулою:

V = S : t

                                25                   5

           25 хв =     год =     год

                                60                 12

5

           22 км :     год = 52,8 км/год

12

 

Відповідь: 52,8 км/год.

 

 

 

 

 

 

                             

 

 

 Підведення підсумків заняття

  На сьогоднішньому уроці ви    ще раз переконались , що математика – всеосяжна наука , без знання якої неможливо пізнати оточуючий нас світ, ні забезпечити науково-технічний   прогрес. Як казав великий   Ейнштейн: «Природа- це реалізація найпростіших математичних ідей».                                    

 

 

                                      Домашнє завдання

Параграф 4 (вивчити правила і означення, спираючись також і на опорний конспект цього уроку) №4.9, 4.23, 4.34, 4.51 (непарні приклади) вислати розв’язки вправ.

Пройти тести і виконати інтерактивні вправи (посилання в дистанційному курсі) – вислати скріншоти результатів.

 

 

Якщо є проблеми при виконанні вправ, можна продивитися відеоуроки

https://www.youtube.com/watch?v=UQH6YFlzyXE https://www.youtube.com/watch?v=3w9gKFSpFKs https://www.youtube.com/watch?v=EJYWkE9ehOU

 

Хто детально хоче розібратися в даній теми і підготуватися до успішної здачі ЗНО, рекомендую такі відеоуроки:

https://www.youtube.com/watch?v=lLYaA_9QQys&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=27

https://www.youtube.com/watch?v=giwIKUxp3Tg&list=PLk91qesJngSK8tu025oH-

3OMaRBXwOmes&index=28&t=4s https://www.youtube.com/user/MathTutor777 https://www.youtube.com/watch?v=m6azW9b0sf4&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=30 https://www.youtube.com/watch?v=WzgsuwQlChM&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=31 https://www.youtube.com/watch?v=7xUjCFcYRvs&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=32 https://www.youtube.com/watch?v=mWwNEWnB9n0&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=33 https://www.youtube.com/watch?v=D93VDRxSoR0&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=34