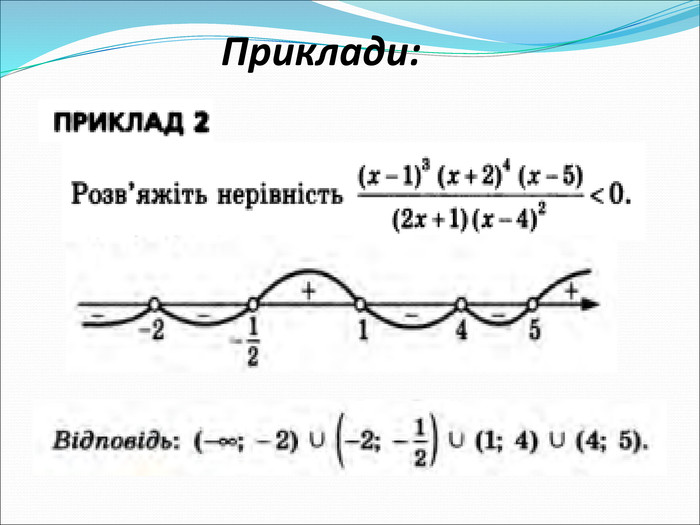
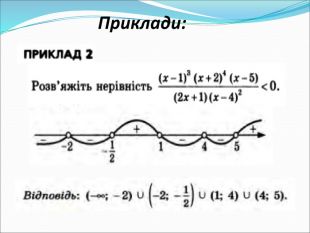
Розв'язування нерівностей методом інтервалів
Про матеріал
Спрощений спосіб розв'язування цілих та дробово-раціональних нерівностей методом інтервалів Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку