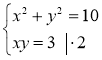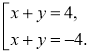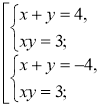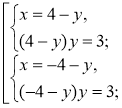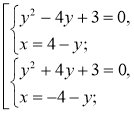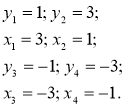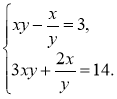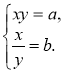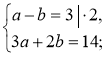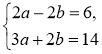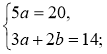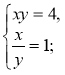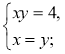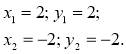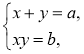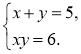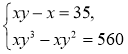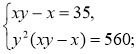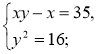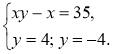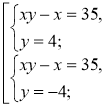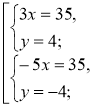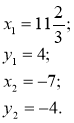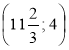Розв'язування систем рівнянь з двома змінними.
Тема уроку. Розв'язування систем рівнянь з двома змінними.
Мета уроку: сформувати в учнів уміння розв'язувати системи нелінійних рівнянь з двома змінними способами: алгебраїчного додавання, заміни змінних, почленного ділення*, а також із застосуванням теореми, оберненої до теореми Вієта*; продовжити роботу із формування вмінь розв'язувати системи, у яких одне з рівнянь є рівнянням першого степеня, способом підстановки. Повторити способи розкладання многочленів на множники та способи розв'язування квадратних та дробово-раціональних рівнянь.
Тип уроку: формування вмінь та навичок.
Наочність та обладнання: опорний конспект № 20 (закінчення).
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Для урізноманітнення роботи з навчальним матеріалом перевірку домашнього завдання можна провести у формі гри «Знайди помилку».
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Необхідність вивчення питання про способи розв'язування нелінійних систем рівнянь стає очевидною, якщо запропонувати учням на цьому етапі уроку виконати два завдання: описати дії при розв'язуванні системи рівнянь, одне з яких є рівнянням першого степеня; після цього запропонувати повторити ті самі дії при розв'язуванні системи, у якій обидва рівняння не є лінійними. Труднощі, які обов'язково виникнуть при спробі виконання запропонованих дій (систему бажано підібрати таким чином, щоб ці труднощі були очевидними), ясно вкажуть учням на те, що постало питання про оволодіння іншими, крім способу підстановки, способами розв'язування систем рівнянь з двома змінними. Ця думка фактично виражатиме основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь учнів і
Усні вправи
- Визначте степінь рівняння:
1) ху + 2у = 3; 2) х2 + у = 5; 3) х2 – 3у2 = 0.
- Виразіть одну змінну через іншу з рівняння:
1) 3х – 5у = 2; 2) 3х – 5у = 0; 3) ху = 5;
4) ![]() = -3; 5) х2 + у – 5 = 0; 6) х + 2у + ху = 4.
= -3; 5) х2 + у – 5 = 0; 6) х + 2у + ху = 4.
- Розкладіть на множники вираз:
1) х2 – у2; 2) х2 – 9; 3) -16х2 + у2;
4) т3 – п3; 5) 8т3 + 27; 6) х2 + 2xy + y2.
- Розв'яжіть систему рівнянь:
1) 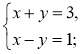 2)
2) 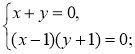 3)
3) 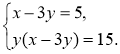
- Поясніть, чому є рівносильними системи рівнянь:
1) 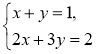 і
і 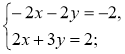 2)
2) 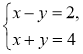 і
і 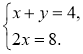
- Розв'яжіть рівняння:
1) х2 + 3x – 4 = 0; 2) х2 – 5х + 6 = 0; 3) ![]() ; 4)
; 4) ![]() .
.
V. Формування знань
План вивчення нового матеріалу
1. Розв'язування систем нелінійних рівнянь з двома змінними способом алгебраїчного додавання.
2. Розв'язування систем нелінійних рівнянь з двома змінними заміною змінних.
3*. Розв'язування систем нелінійних рівнянь з двома змінними способом почленного ділення.
4*. Розв'язування систем нелінійних рівнянь з двома змінними із застосуванням теореми, оберненої до теореми Вієта.
Опорний конспект № 20 (продовження, початок див. урок № 31)
|
Розв'язування систем нелінійних рівнянь з двома змінними способом алгебраїчного додавання |
|
|
Приклад: |
Коментар |
|
1. х2 + 2ху + у2 = 16; (х + у)2 = 16; |
1. Помножимо друге рівняння на 2 і додамо до першого. |
|
2.
|
2. Розв'яжемо окремо дві системи, у яких одне з рівнянь є лінійним. |
|
Відповідь: (3; 1); (1; 3); (-3; -1); (-1; -3). |
|
|
Розв'язування систем нелінійних рівнянь з двома змінними заміною змінних |
|
|
Приклад: |
Коментар |
|
1.
|
1. Зробимо заміну ху = а; |
|
2. Відповідь: (2; 2); (-2; -2). |
2. Виконаємо обернену заміну і розв'яжемо систему способом підстановки. |
|
Розв'язування систем рівнянь виду де а і b — деякі відомі числа, із застосуванням теореми, оберненої до теореми Вієта |
|
|
Приклад. Розв'яжемо систему рівнянь Відповідь: (2; 3); (3; 2). |
|
|
Розв'язування систем нелінійних рівнянь з двома змінними способом почленного ділення рівнянь системи |
|
|
Приклад: |
Коментар |
|
1. |
1. Розкладемо на множники друге рівняння та поділимо його на перше почленно. |
|
2.
Відповідь: |
2. Розв'яжемо дві системи.
|
Методичний коментар
Матеріал даного уроку є основою для подальшого вивчення у наступних класах способів розв'язування систем тригонометричних, показникових, логарифмічних та ірраціональних рівнянь. Як відомо, основними способами розв'язування цих систем є спосіб підстановки і спосіб заміни змінних. Тому вивчення цих способів та оволодіння учнями навичками їх використання є обов'язковими у 9 класі. Проте оволодіння іншими, запропонованими в опорному конспекті № 20 способами розв'язування систем рівнянь суттєво розширює спектр засобів, які допоможуть майбутнім випускникам більш раціонально розв'язувати відповідні задачі під час виконання завдань ДПА (див., наприклад, розв'язування систем рівнянь з двома змінними із застосуванням теореми, оберненої до теореми Вієта).
На даному уроці вивчення способів розв'язування систем нелінійних рівнянь з двома змінними проводиться на конкретних прикладах відповідних систем і фактично спирається на ті знання про властивості систем, які учні отримали у 7 класі під час вивчення способів розв'язування систем лінійних рівнянь з двома змінними. Тому для кращого розуміння учнями змісту дій перед вивченням матеріалу уроку бажано повторити основні властивості рівносильних систем, зміст дій при розв'язуванні систем лінійних рівнянь способом додавання, а також способи розв'язування основних видів раціональних рівнянь (див. етап актуалізації опорних знань та вмінь).
Зауважимо, що для свідомого володіння учнями вивченими способами розв'язування систем нелінійних рівнянь з двома змінними після розгляду кожного зі способів учитель має наголосити на тому, що всі ці способи спрямовані лише на одне: перехід від даної системи нелінійних рівнянь до сиетеми рівнянь, у яких хоча б одне з рівнянь є лінійним.
VI. Відпрацювання вмінь
Письмові вправи
Зміст письмових вправ уроку може бути таким:
- розв'язати системи нелінійних рівнянь з двома змінними способом алгебраїчного додавання;
- розв'язати системи нелінійних рівнянь з двома змінними заміною змінних;
- * розв'язати системи нелінійних рівнянь з двома змінними способом почленного ділення;
- розв'язати системи нелінійних рівнянь з двома змінними із застосуванням теореми, оберненої до теореми Вієта;
- на повторення: розв'язування систем рівнянь з двома змінними, одне з яких є лінійним, способом підстановки.
VII. Підсумки уроку
Контрольне запитання
У який спосіб можна розв'язати систему рівнянь:
1) 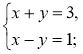 2)
2) 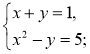 3)
3) 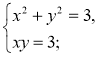 4)
4) 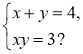
VIII. Домашнє завдання
- За опорним конспектом № 20 повторити, які способи дій можна застосовувати при розв'язуванні систем рівнянь з двома змінними.
- Розв'язати вправи, аналогічні за змістом вправам класної роботи.
- Повторити: зміст поняття графіка рівняння з двома змінними та схему дій при побудові графіка рівняння з двома змінними.

про публікацію авторської розробки
Додати розробку