Розв'язування текстових задач складанням систем рівнянь з двома змінними.

Тема уроку. Розв'язування текстових задач складанням систем рівнянь з двома змінними.

Мета уроку: закріпити знання учнів про загальну схему розв'язування тек­стових задач складанням систем рівнянь з двома змінними; доповнити ці знання уявленням про спосіб міркувань при розв'язуванні задач на відсотковий склад речовин. Працю­вати над виробленням навичок розв'язувати за загальною схемою текстові задачі різного змісту (арифметичні, геометричні, задачі на рух та на сумісну роботу, а також задачі на відсотковий склад речовин). Працювати над вдосконаленням навичок розв'язування систем нелінійних рівнянь з двома змінними різними способами.

Тип уроку: відпрацювання вмінь та навичок.

Наочність та обладнання: опорний конспект № 21.

Хід уроку

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

Для урізноманітнення роботи з навчальним матеріалом на цьо­му етапі уроку можна провести гру «Знайди помилку» або для усвідомленого виконання роботи з перевірки правильності вико­нання завдань домашньої роботи й, можливо, корекції знань та вмінь учнів пропонуємо учням, використовуючи записи, виконані вдома, заповнити таблицю:

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Учитель повідомляє учням, що відповідно до програми з мате­матики вони мають оволодіти способом розв'язування ще одного виду задач на складання систем рівнянь з двома змінними. Можна запропонувати приклад однієї з таких задач зі збірника завдань для ДПА з алгебри за 9 клас.

Задача

Змішавши 20-відсотковий та 60-відсотковий розчини кислоти, отримали 800 г розчину, що містить 30 % кислоти. Скільки грамів кожного розчину змішали?

Після обговорення змісту задачі та ідей щодо її розв'язування формулюється завдання на урок: сформувати вміння розв'язувати задачі, аналогічні за змістом, складанням систем рівнянь з двома змінними.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Запишіть у вигляді десяткового або звичайного дробу:
   1) 1%; 2) 2%; 3) 10%; 4) 25%;   5) 50%; 

6) 75%; 7) 125%.

2. Знайдіть:
   1.   25% від числа 360;
   2.   число, якщо 75% його становлять 0,3;
   3.   скільки відсотків становить число 25 від числа 40; число 40 від числа 25.
3. Розв'яжіть систему рівнянь:

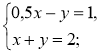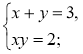1)    2)   3)

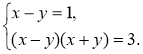
V. Формування знань

Опорний конспект № 22

Методичний коментар

Спосіб міркувань, покладений в основу розв'язування задач на відсотковий склад речовини, ґрунтується на знаннях та вмін­нях, набутих учнями при вивченні теми «Відсотки» у 6 класі. Сам спосіб цих міркувань спочатку демонструється на прикладі розв'язання конкретної текстової задачі. Після цього формулюєть­ся орієнтовна схема дій при розв'язуванні задач подібного виду, яку краще за все записати у вигляді таблиці (див. опорний кон­спект № 22). Кращому розумінню виконаного при розв'язуванні задачі способу міркувань сприятиме розв'язання вправ на повто­рення (див. етап актуалізації опорних знань та вмінь).

VI. Відпрацювання вмінь

Письмові вправи

Зміст письмових вправ уроку може бути таким:

1. розв'язати задачі на відсотковий склад речовин;
2. розв'язати задачі різного змісту на складання систем рівнянь з двома змінними;
3. на повторення: вправи на застосування різних способів розв'я­зування систем рівнянь з двома змінними.

VII. Підсумки уроку

Учні складають список видів задач, що розв'язуються за до­помогою систем рівнянь з двома змінними.

VIII. Домашнє завдання

1. Повторити матеріал розділу «Системи рівнянь з двома змінни­ми вищих степенів».
2. Виконати самостійну роботу (див. нижче) за варіантом, указа­ним учителем.

Самостійна робота

Варіант 1

1. Складіть систему рівнянь за умовою задачі.

1. Сума двох чисел х і у дорівнює 12, а їхній добуток дорів­нює 35. Знайдіть ці числа.
2. Висота х прямокутника на 14 см більша за його основу у. Знайдіть сторони прямокутника, якщо його діагональ до­рівнює 13 см.
3. Маса одного зі сплавів цинку х кг, а другого — у кг. Яка маса кожного із цих сплавів, якщо перший містить 9%, а другий — 30% цинку і при їх змішуванні утворюється 300 кг сплаву, що містить 23 % цинку?
4. Один комбайнер збирає врожай з ділянки за х год, а дру­гий — за у год. При одночасній роботі вони збирають урожай з цієї ж ділянки за 3 год 45 хв. За скільки годин може виконати, завдання кожний із комбайнерів, працюю­чи окремо, якщо відомо, що перший виконує це завдання на 4 год швидше, ніж другий?

2. Розв'яжіть задачу, склавши та розв'язавши систему рівнянь.

1. Одне з чисел на 7 більше від другого, їхній добуток дорів­нює 12. Знайдіть ці числа.
2. Периметр прямокутника дорівнює 28 см, його площа ста­новить 45 см². Знайдіть сторони прямокутника.
3. Скільки грамів 4-відсоткового і 10-відсоткового розчинів солі треба взяти, щоб отримати 180 грамів 6-відсоткового розчину солі?
4. Одна з дорожніх бригад може заасфальтувати деяку ділян­ку дороги на 4 год швидше, ніж друга. За скільки годин може заасфальтувати цю ділянку кожна з бригад, працюю­чи окремо, якщо відомо, що за 24 год сумісної роботи вони заасфальтували 5 таких ділянок?

Варіант 2

1. Складіть систему рівнянь за умовою задачі.

1. Різниця двох чисел х і у дорівнює 2, а їхній добуток до­рівнює 48. Знайдіть ці числа.
2. Висота х прямокутника на 2 см менша за його основу у. Знайдіть сторони прямокутника, якщо його діагональ до­рівнює 10 см.
3. Маса одного зі сплавів міді х кг, а другого — у кг. Яка маса кожного із цих сплавів, якщо перший містить 20 %, а другий — 50 % міді і при їх змішуванні утворюється ЗО кг сплаву, що містить 30% міді?
4. 3) Один комбайнер збирає врожай з ділянки за х год, а дру­гий — за у год; при одночасній роботі вони збирають врожай з цієї ж ділянки за 16 год. За скільки годин може виконати завдання кожний із комбайнерів, працюючи окремо, якщо відомо, що перший виконує це завдання на 24 год повіль­ніше, ніж другий?

2. Розв'яжіть задачу, склавши та розв'язавши систему рівнянь.

1. Одне із чисел на 5 менше від другого, їхній добуток до­рівнює 36. Знайдіть ці числа.
2. Периметр прямокутної ділянки дорівнює 200 м, його площа становить 2400 м². Знайдіть довжину та ширину ділянки.
3. Скільки грамів 3-відсоткового і 8-відсоткового розчинів солі треба взяти, щоб отримати 260 грамів 5-відсоткового розчину солі?
4. 3 населених пунктів А і В, що розташовані на відстані 50 км один від одного, виїхали одночасно два мотоцикліс­ти і зустрілись через 30 хв. Знайдіть швидкість кожного із них, якщо відомо, що один із них прибув у пункт А на 25 хв раніше, ніж другий прибув у пункт В.