Що таке фрактали? Світ навколо нас.

Схожі форми зустрічаються всюди, від мікро- до макросвіту: в мінералах, рослинах і тваринному світі, в структурі ДНК, в природних явищах (циклони, блискавки, берегові лінії), планетарних системах і зоряних скупченнях. Вони присутні і в живих організмах.

Які закономірності і в чому причина такої подібності? Поясненням цьому є фрактал. 

Фрактальність також простежується як у самій людині, так і у взаємовідносинах у родині, колективі, суспільстві. Наша Галактика за формою схожа на раковину Наутилуса, людське око на космічну туманність, а клітини мозку на весь наш Всесвіт.

Чи доводилося бачити схожі форми у живих і неживих об’єктах? Ніби одна і та ж формула, пронизує все навколо.

Фрактал (лат. «fractus» — подрібнений) — самоподоба (копіювання)

геометричних фігур, де кожен фрагмент дублюється в масштабі, що зменшується. Можна сказати, що фрактал — це візерунок, який повторює сам себе в різних масштабах до нескінченно малого або/та нескінченно великого. 

Він народжується не просто повторенням форм, а скоріше повторенням процесу, який застосовується до форми. Нескінченний ланцюжок самопобудови.

У природі яскравим прикладом такого візерунка є капуста сорту «Романеско».

На даний момент нам не відомо, яким терміном називали наші предки явище самоподібності об’єктів. Але точно можна сказати, що знання про фрактали входили до розділу «сакральної геометрії» минулого. Розуміння математичної закономірності всього світопорядку було природним ще тисячоліття назад.

Наприклад, видатному зодчому Старовинниго Єгипту Імхотепу вдалося звести першу ступінчасту піраміду — грандіозне фрактальне спорудження з чіткими математичними пропорціями. 

Група близьких Імхотепу людей називали Бога не інакше як

Великим Зодчим Всесвіту. А за часів існування ордена Тамплієрів по всій Європі набув широкого поширення готичний стиль архітектури — втілення сакральної геометрії і фрактальних візерунків у камені.

В області вивчення фракталів ще в кінці ХIX — початку ХХ століть працювали багато вчених: П’єр Фату, Жюль Анрі Пуанкаре, Георг Кантор, Фелікс Гаусдорф, Гастон Жюліа.

Вони і заклали математичну базу для появи теорії фракталів. Поява обчислювальних пристроїв дозволила прискорено проводити ітерації (багаторазово повторюваний процес

обчислення) і візуалізувати формули. А сама ідея ввести

формулу Гастона Жюліа в комп’ютер і за його допомогою провести громіздкі розрахунки прийшла в голову

Мандельброту приблизно в 1977 році. Раз за разом, змінюючи змінну C, він отримував нові дивовижні зображення. Таким чином, множини Жюліа набули геометричних форм.

деякі з них: ¨ геометричні;

¨  алгебраїчні;

¨ 

¨  концептуальні (соціокультурні, непросторові і т.д.)

¨  Геометричні види фракталів є найбільш наочними і простими в будові. Побачити їх може будь-яка людина. 

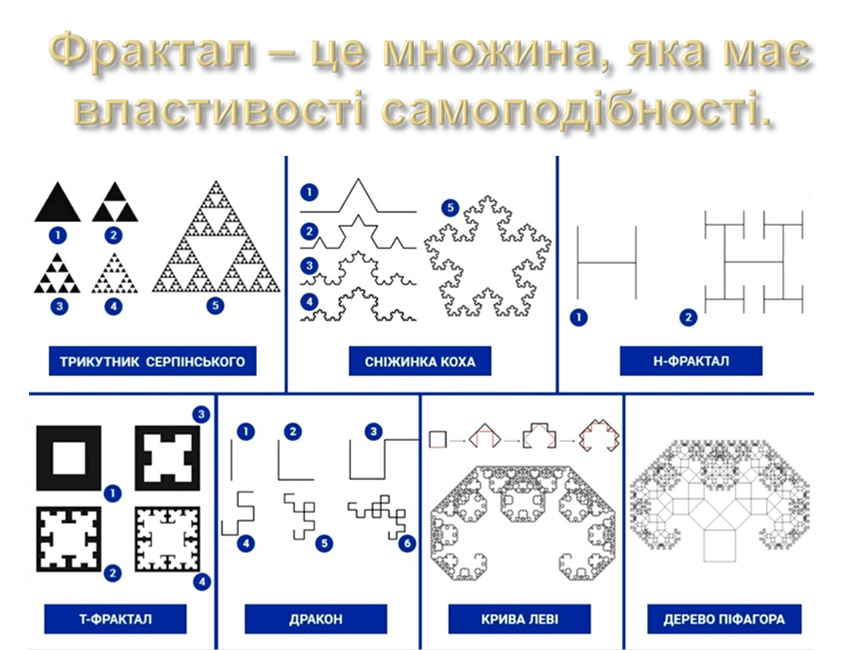
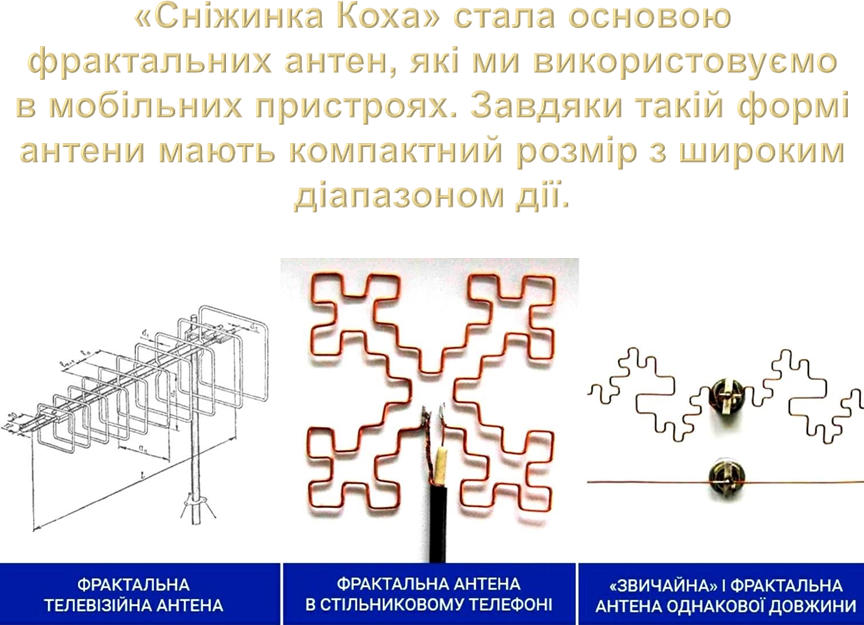
¨  Безліч таких фракталів можна намалювати на звичайному аркуші паперу в клітинку. Прикладом є: Трикутник Серпінського, Сніжинка Коха, Н-фрактал, Т-фрактал, Дракон, Крива Леві, Дерево Піфагора.

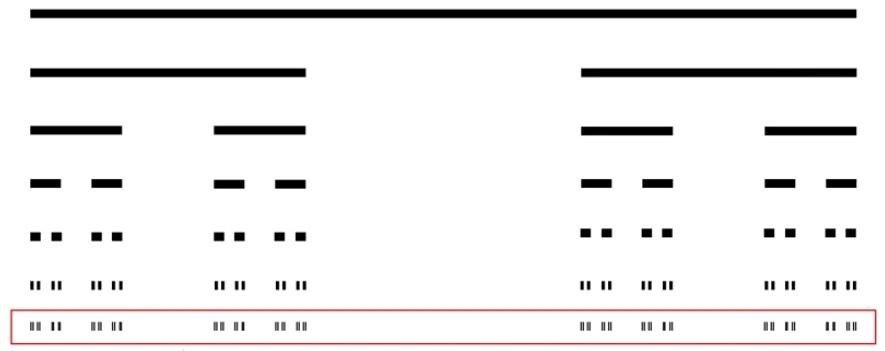
Розглянемо принцип побудови фракталів на прикладі — «Сніжинки Коха». Він будується шляхом багаторазового поділу лінії відрізка на 3 рівні частини і заміни середньої частини на 2 нових відрізка тієї ж довжини. 

Число сторін кожен раз почетверяється, внаслідок чого стає нескінченно великим. Периметр сніжинки має нескінченну довжину, але площа при цьому кінцева, оскільки фігура є замкнутою.

За принципом побудови цікавий також «Трикутник Серпінського». Візьмемо рівносторонній трикутник, відзначимо середини його сторін.

З’єднаємо серединні точки прямими лініями.

Утворилися 4 трикутника.

Центральний трикутник виймаємо і «викидаємо».

Тепер повторимо цю операцію з кожним із новоутворених трикутників. 

І так до нескінченності!

¨   Це найбільша група фракталів, яка базується на основі різних алгебраїчних формул. Яскравим прикладом є фрактал Мандельброта. Нині їх прийнято відображати в кольорі. 

¨   Виходять дуже красиві незвичайні орнаменти, які використовують, наприклад, в дизайні одягу.

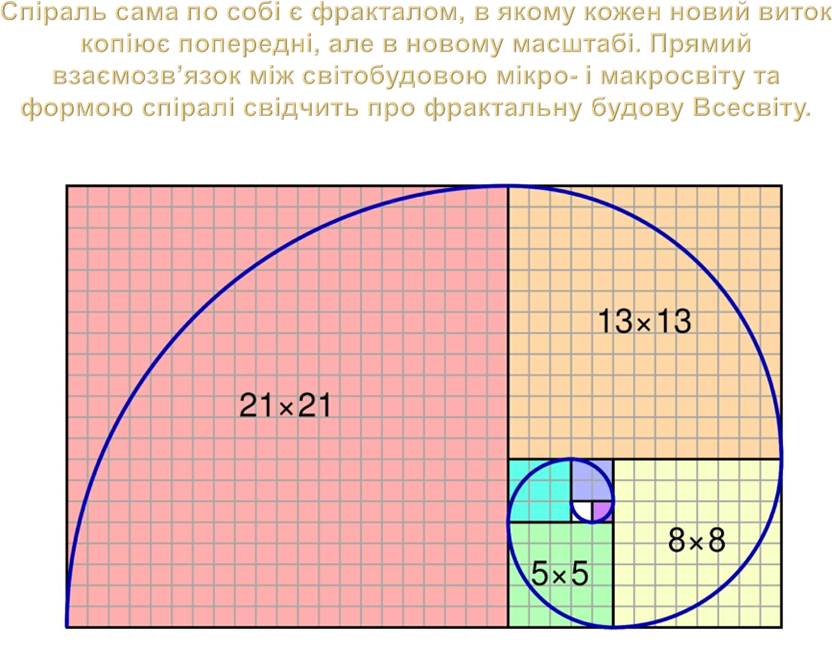
¨   Світ навколо нас різноманітний. Багато об’єктів, що існують в природі, є фракталами. В їхній основі лежить Божественна пропорція (число Фі) — це Золотий перетин і золота спіраль, завдяки якій ми сприймаємо красу і гармонію природи, пропорційність будови людини, древньої архітектури, класичних творів мистецтва.

¨   Золота спіраль будується фрактальним способом: прямокутник із золотою пропорцією. 1,618 (число Фі) розбивають на малі квадрати і проводять дугу. Тобто в спіралях велика дуга переходить у подібну меншу і т.

Будуються шляхом хаотичної зміни деяких параметрів.

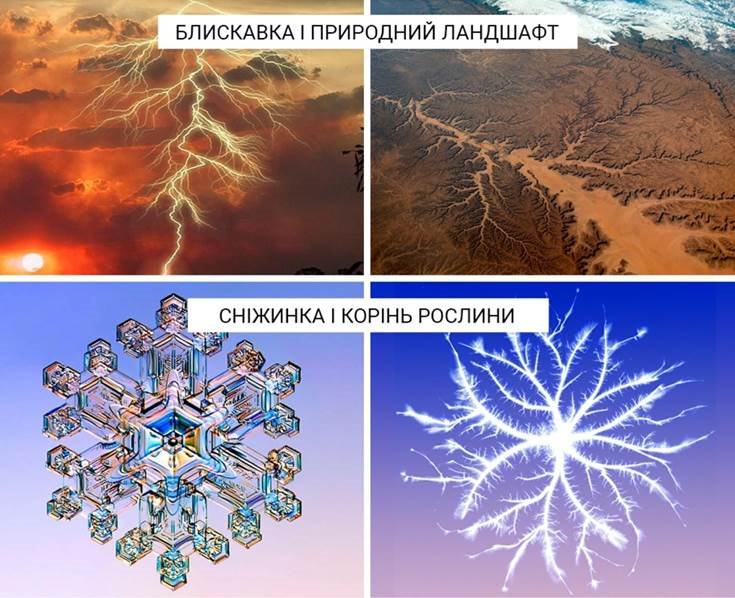
При цьому виходять об’єкти, дуже схожі на природні. Фрактали даного виду широко застосовуються в кіноіндустрії: за допомогою комп’ютерної графіки створюються штучні гори, хмари, поверхні моря, планети, берегові лінії, несиметричні дерева. 

Також представником даного виду є — «плазма» в природі: • Блискавка

•         Іоносфера

•         Північне сяйво

•         Полум’я

Цей вид об’єднує непросторові структури, що виходять за рамки геометричної фрактальності. Принцип багаторівневої самоподібності закладений в культурних творах. У художніх текстах (віршах для дітей, народних піснях, у музичних творах і казках) часто зустрічається «оповідання в оповіданні».

Фрактальність спостерігається в організації людських поселень (країна — місто — квартал); у розподілі суспільства на групи (народ — соціокультурна група — сім’я — людина).

 Сюди ж віднесемо фрактальність взаємовідносин, які починаються з самої людини. 

Змінюється людина, її сприйняття, внутрішній стан — змінюються взаємовідносини в сім’ї, колективі, в результаті перетворюється все суспільство. Простежується фрактальність в ієрархічних системах управління.

Науці вже відомо про спіральні структури і спіралеподібний рух енергії. У цьому русі також виявляються фрактальні властивості. Їх можна побачити в космосі, в тілі людини, в рослинах і природних явищах (хмари, циклони, вири). Фізики спостерігали, як в турбулентних потоках великі вихори породжують вихори поменше, а ті ще менше, і таке ділення спіралеподібних енергій спостерігалося до тих видимих меж, які технічно були доступні вченим.

Фрактальні властивості присутні в структурі та русі енергії електричного розряду, води, в рості рослин і т. д.

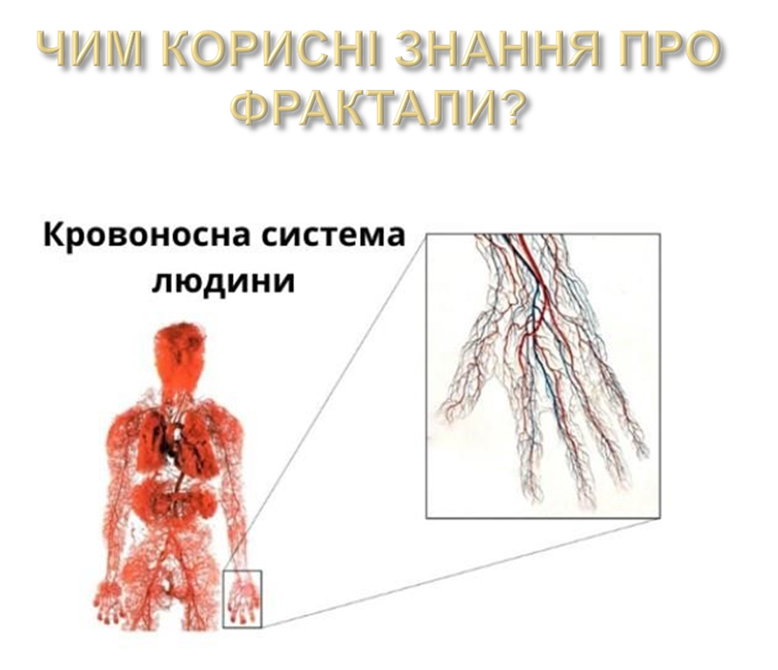
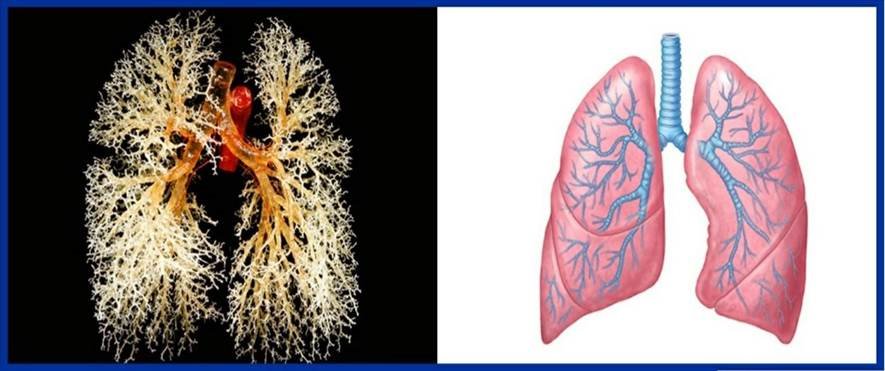
Як бачимо, фрактали — це не щось відокремлене і незрозуміле. Вони наповнюють наше життя.

 Знання про фрактальну побудову світу були у людей з давніх-давен. 

Ми провели невелике дослідження і знайшли цікаві факти, пов’язані з давниною фракталів, способами їх застосування в архітектурі і проявів як в самій людині, так і в суспільстві