ШИФРУВАННЯ ІНФОРМАЦІЇ З ВИКОРИСТАННЯМ МАТЕМАТИЧНИХ МЕТОДІВ

 

 

Відділення: математика Секція: прикладна математика, математичне моделювання

 

 

Шифрування інформації з використанням

 математичних методів

 

 

Роботу виконала: Науковий керівник:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

Перелік термінів…………………………………………….........3

Вступ…………………………………………………………............4

Розділ І Захист інформації

1.           Історія виникнення шифрування…………………………..6
2.           Сфери застосування шифрування………………………….8

Розділ ІІ Шифри

2.1. Шифри заміни……………………………………………….12

2.2. Цифрові і табличні шифри………………………………….14

2.3. Шифри перестановки………………………………………..15

2.4. Матричні шифри……………………………………………..16

2.5. Арифметика остач……………………………………..….....17

2.6. Шифрування та дешифрування за допомогою EXCEL……18

7. . Розробка завдань для формування практичних навичок

шифрування……………………………………………………24

     

Висновки……………………………………………….…….........25

Список використаних джерел…..………………………..27

ДОДАТКИ

 

 

 

 

ПЕРЕЛІК ТЕРМІНІВ

Дешифрування	це обернений процес відтворення інформації із шифротексту
Захист інформації	сукупність методів і засобів, що забезпечують цілісність, конфіденційність і доступність інформації за умов впливу на неї загроз природного або штучного характеру, реалізація яких може призвести до завдання шкоди власникам і користувачам інформації.
Ключ	це секретний параметр (в ідеалі, відомий лише двом сторонам) для окремого контексту під час передачі повідомлення
Кодування	це перетворення звичайного, зрозумілого, тексту в код (виконується без ключа)
Криптоаналіз	розділ криптології, що займається математичними методами порушення конфіденційності і цілісності інформації без знання ключа
Криптографія	наука про математичні методи забезпечення конфіденційності і автентичності інформації
Криптографічний захист інформації	вид захисту інформації, що реалізується за допомогою перетворень інформації з використанням спеціальних даних (ключових даних) з метою приховування (або відновлення) змісту інформації, підтвердження її справжності, цілісності, авторства тощо
Шифр, або криптографічний алгоритм	це математична формула, що описує процеси шифрування і розшифрування
Шифрування	це спосіб зміни повідомлення або іншого документа, що забезпечує спотворення його вмісту

ВСТУП

Як тільки люди навчилися писати, у них відразу ж з'явилося бажання зробити написане зрозумілим не всім, а тільки вузькому колу. Навіть у найбільш древніх пам'ятниках писемності вчені знаходять ознаки навмисного спотворення текстів: зміна знаків, порушення порядку запису і т. д. Процес перетворення тексту, написаного загальнодоступною мовою, в текст, зрозумілий тільки адресату, називають шифруванням, а сам спосіб такого перетворення називають шифром. Але якщо є бажаючі приховати зміст тексту, то знайдуться і охочі його прочитати. Методи читання таких текстів вивчає наука криптоаналіз. Хоча самі методи криптографії та криптоаналізу донедавна були не дуже тісно пов'язані з математикою, в усі часи багато відомих математиків брали участь в розшифровці важливих повідомлень. І часто саме вони домагалися помітних успіхів, адже математики у своїй роботі постійно мають справу з різноманітними і складними завданнями, а кожен шифр - це логічна задача. Поступово роль математичних методів в криптографії стала зростати, і за останнє сторіччя вони істотно змінили цю древню науку. Термін «криптографія» далеко пішов від свого початкового значення - «тайнопис», «таємний лист». Криптографія об'єднує методи захисту інформації абсолютно різного характеру, які спираються на перетворення даних по секретним алгоритмам.

Актуальність дослідження. В умовах сучасного інформаційного суспільства  проблема захисту інформації гостро постає перед людством. Саме технології шифрування, які базуються на математичних методах,  є останньою лінією оборони та забезпечують безпеку інформаційних даних.

Гіпотеза: процес шифрування, найбільш надійний спосіб захисту інформації, відбувається за допомогою математичних методів.

Мета дослідження: з'ясувати, в чому полягає зв'язок математичних методів і процесу шифрування. Виходячи з мети поставлені наступні завдання дослідження: вивчити літературу та Internet ресурси з теми; проаналізувати отриману інформацію; дослідити за допомогою яких математичних методів відбувається процес шифрування; попрактикуватися в шифруванні.

Методи дослідження: аналіз інформації, математичне моделювання.

За об'єкт дослідження взято процес шифрування,  предметом дослідження є характеристика математичних методів та математичне моделювання

Історіографія. В історичній та математичній літературі дана тема досить добре опрацьована, оскільки вивчення історії шифрів та процесу шифрування необхідно для черпання ідей для її розвитку  сьогодні. Матеріалом для написання роботи послужила, в першу чергу, книга А.П. Алфьорова, А.Ю. Зубова А.С. Кузьміна і А.В. Черьомушкіна «Основи криптографії» [1], в якій подано докладний історичний нарис раннього розвитку криптографії. Для опису криптографії в нинішньому світі використовувалася книга Барічева С.Г., Гончарова В.В. і Сєрова Р.Е. «Основи сучасної криптографії» [2]. Стаття Жельнікова В., «Криптографія від папірусу до комп'ютера» [3] послужила джерелом цікавих прикладів. В книзі Дориченка С.А. та Ященко В.В. «25 этюдов о шифрах» [4] в загальнодоступній формі описані основні поняття криптографії, запропоновані необхідні відомості з математичного апарату криптографії, крім того, як приклади розібрані шифри, добре відомі з історії та детективної літератури.

 

 

 

 

 

 

РОЗДІЛ І

ЗАХИСТ ІНФОРМАЦІЇ

 

1.           Історія виникнення шифрування

Те, що інформація має цінність, люди усвідомили дуже давно. Тоді і виникло завдання захисту від надмірно цікавих людей. В стародавні часи люди намагалися використовувати для вирішення цього завдання найрізноманітніші методи, і одним з них був тайнопис - уміння складати повідомлення так, щоб його сенс був недоступний нікому окрім посвячених в таємницю. Мистецтво тайнопису зародилося ще в доантичні часи і проіснувало аж до зовсім недавнього часу, лише декілька десятиліть тому все змінилося корінним чином - інформація придбала самостійну комерційну цінність і стала широко поширеною, майже звичайним товаром. Початок криптографії збігається з початком писемності, так як написаний текст міг зрозуміти тільки вміє читати.

Шифрування з'явилося приблизно чотири тисячі років тому. Першим відомим застосуванням шифру (коду) вважається єгипетський текст, датований приблизно 1900 р. до н. э., автор якого використовував замість звичайних (для єгиптян) ієрогліфів не співпадаючі з ними знаки.

Першим описав використання шифрувального пристрою Плутарх, першим дешифрувальником був Аристотель. Розквіт криптографії припадає на середні віки. Один із середньовічних шифрів протримався до Другої світової війни.  В XVII-XVIII століттях стає все більш зрозуміло, що захист інформації - не стільки мистецтво твору й відгадування витончених шифрів, скільки точна наука. Усе помітніше перехід криптографії з області чорної магії в область чистої математики. Ми майже нічого не знаємо про те, чи займалися провідні математики того часу проблемами шифрування й дешифрування, але є дані, що деякі з них володіли криптографією. Серед них Блез Паскаль, що зробив ряд відкриттів в області комбінаторики й метод, що створив, індуктивного доказу; Ісаак Ньютон і Готфрид Лейбніц, що розробили диференціальне й інтегральне числення. Відомий  англійський філософ Ф. Бекон запропонував ідею двійкового кодування. Леонард Ейлер вів великі дослідження з перерахування й побудови латинських квадратів, тобто шифрів заміни. Деякі історики вважають однією з причин невдалого закінчення для Росії Першої світової війни некоректне ставлення до шифрів. Математик Франсуа Вієт, будучи молодим офіцером розвідки, знайшов ключ до шифру іспанського короля, що містив 500 символів. Іспанці, не повіривши, що шифр можна було розгадати, звернулися зі скаргою до Папи Римського, звинувачуючи французів в чаклунстві. В XIX столітті французький філолог Ж.Ф. Шамполь, розшифрував ієрогліфи стародавніх єгиптян. В XX столітті О. В Кнозоров, лінгвіст, історик і етнограф, розшифрував писемність стародавнього народу майя.

Диск Енея – криптографічний інструмент для захисту інформації. Використовувався у ІV ст. до нашої ери.Механізм шифрування простий. Необхідно було по черзі простягати вільний кінець нитки через отвори, що означають літери. У результаті диск із затягненою в нього ниткою і був зашифрованим посланням.

 

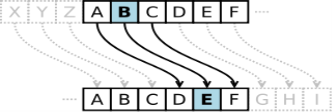
  Один з найвідоміших методів шифрування носить ім'я Цезаря, який якщо і не сам його винайшов, то активно їм користувався. Не довіряючи своїм посильним, він шифрував листи елементарною заміною А на D, В на Е і так далі по всьому латинському алфавіту. При такому кодуванні комбінація XYZ була б записана як АВС (прямий код N+3). З початком застосування електронних способів передачі та обробки інформації задачі криптографії почали розширюватися. В даний час, коли комп'ютерні технології знайшли масове застосування, проблематика криптографії включає численні завдання, які не пов'язані безпосередньо з засекречуванням інформації.  

 

2.           Сфери застосування шифрування.

Думка про те , що людина в своєму житті не часто зустрічається з шифруванням є помилковою. Ми кожного дня бачимо різноманітні шифри та коди , але не завжди помічаємо їх . З точки зору криптології, живий організм є складною криптосистемою (зашифрована інформація міститься в генах). Прикладом застосування методів дешифрування і сучасних технологій створення штучного інтелекту є метод крипто аналізу (наука про методи дешифрування) за допомогою генетичних алгоритмів.

Сфера комерційної діяльності.

До шифрування інформації належить звичайний штрих-код, який є шифром. Кодування та маркування штриховими кодами виду послуг, їх вартості та термінів оплат дозволяє автоматизувати облік надання послуг та контроль їх оплати. Маркуванню підлягають як товари так і самі послуги, наприклад, комунальні послуги, послуги зв'язку, пошти, страхових компаній. Електронні контрольно-касові апарати, обладнані сканерами для зчитування штрихових кодів, дозволяють: забезпечити швидкий і безпомилковий розрахунок з покупцями; видавати касовий чек із переліком куплених товарів та їх ціни; ліквідувати черги та підвищити рівень обслуговування покупців; оперативно передавати інформацію про продаж товарів до системи обліку.

 

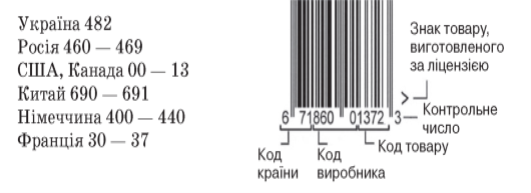
Мал.1.1.Схема штрих-коду

Електронний квиток або e-ticket - це електронний документ, що засвідчує договір перевезення між пасажиром і перевізником. На відміну від паперового квитка, електронний квиток являє собою цифровий запис в базі даних компанії. Придбаний за технологією “online ticket” квиток містить в собі унікальний штрих-код. Закодована на електронному квитку інформація перевіряється сканером штрих-кодів. Після успішної перевірки по даному квитку може бути дозволений вхід. Система сканування не пропускає повторів або використання одного і того ж штрих-коду двічі.

ТЕРМ.№2301	ПОСАДОЧНИЙ ДОКУМЕНТ				000B3E60-87DE-053A-0001		ПН:400758126555 ФН:3000182012 ЗН:ЗТ00000003 ФК:24815881
	ПАТ «УКРЗАЛІЗНИЦЯ» м. Київ, вул. Тверська, буд.5				#749-Е1-3696273-1906
МПС	ЦЕЙ ПОСАДОЧНИЙ ДОКУМЕНТ Є ПІДСТАВОЮ ДЛЯ ПРОЇЗДУ						19.06.2018 19:28
Прізвище, Ім'я			Чапкіна Юлія			Поїзд	146 ШБ  HШ
Відправлення		2208580	ІЗМАЇЛ			Вагон	14 П П-З
Призначення		2208001	ОДЕСА-ГОЛОВНА			Місце	015 Пільговий
Дата/час відпр.			20.06.2018 17:25			Сервіс	БIЛ БЕЗ КОНДИЦIОНУВАННЯ
Дата/час приб. 145*			20.06.2018 23:23
ВАРТ=53,91ГРН(КВ.11,22+ПЛ.7,02+СП.25,00+ПДВ.8,97+СТР.0,03+КЗБ.1,67) В Т.Ч. БIЛ-30,00 (З ПДВ) #ДОКУМЕНТ ПІЛЬГОВИКА: ПІЛЬГ СТУД СК09327069 #СТР.ВIД Н/В 6000НЕОП.МIН. СК"АРСЕНАЛ СТРАХУВАННЯ", КИЇВ БОРЩАГІВСЬКА154, T0800604453 ЧАС ВІДПРАВЛЕННЯ КИЇВСЬКИЙ
				Цей посадочний документ є підставою для проїзду без звернення в касу. Посадочний документ є розрахунковим документом. Посадка здійснюється за пред'явленням документа, який посвідчує особу. Повернення цього посадочного документа можливе до відправлення поїзда.

  Мал.1.2 Бланк електронного квитка

Сфера державного управління.

Кожна людина має ідентифікаційний код або індивідуальний податковий номер, який  є важливим документом у сучасному світі. Без нього ми не можемо отримати кредит, оформити нотаріальну довіреність або купівлю-продаж, здійснити інші дії. Незважаючи на те, що отримання ідентифікаційного коду є добровільною процедурою, його вимагають у багатьох інстанціях. Ідентифікаційний номер складається з десяти цифр: перші п'ять із них визначають дату народження власника номера -  п'ятизначне число є кількістю днів від 31 грудня 1899 року до дати народження особи, наступні 4 цифри (включаючи передостанню) -  означають порядковий номер людини, що народилася в цей день, передостання цифра визначає стать власника: якщо цифра непарна, стать – чоловіча, якщо парна – жіноча, десята цифра – контрольна.

Мал.1.3. Ідентифікаційний код

Розвиток глобальних комунікацій в діловому і повсякденному житті привів до появи нової області взаємовідносин, предметом яких є електронний обмін даними. У такому обміні даними можуть брати участь органи державної влади, комерційні і некомерційні організації, а також громадяни в своїх офіційних і особистих стосунках. Проблема збереження електронних документів від копіювання, модифікації і підробки вимагає для свого вирішення специфічних засобів і методів захисту. Одним з поширених в світі засобів такого захисту є Електронний цифровий підпис (ЕЦП), який за допомогою спеціального програмного забезпечення підтверджує достовірність інформації документу, його реквізитів і факту підписання конкретною особою. Електронний підпис — дані в електронній формі, які додаються до інших електронних даних або логічно з ними пов'язані та призначені для ідентифікації підписувача цих даних. Електронний цифровий підпис - вид електронного підпису, отриманого за результатом криптографічного перетворення набору електронних даних, який додається до цього набору або логічно з ним поєднується і дає змогу підтвердити його цілісність та ідентифікувати підписувача. Електронний цифровий підпис накладається за допомогою особистого ключа та перевіряється за допомогою відкритого ключа.

Також процес шифрування застосовується у військовій справі та юридичній діяльності, в сфері медичного обслуговування.  Всі ми сьогодні, іноді навіть не підозрюючи про це, застосовуємо засоби захисту інформації - шифруємо повідомлення електронної пошти та  користуємося електронними банківськими картками.

Реєстрування для участі в зовнішньому незалежному оцінюванні,  створення та оформлення реєстраційної картки.

В наступному році  я повинна буду проходити зо́внішнє незале́жне оці́нювання ЗНО— іспити для вступу до вишів в Україні.

Комплекс організаційних процедур (передусім — тестування) спрямований на визначення рівня навчальних досягнень випускників середніх навчальних закладів при їхньому вступі до закладів вищої освіти. Щоб успішно зареєструватися для участі в зовнішньому незалежному оцінюванні, необхідно створити та оформити реєстраційну картку, сформувати пакет документів і передати його до регіонального центру.

РОЗДІЛ ІІ

ШИФРИ

У шифрів пов'язаних з різними арифметичними операціями є один істотний недолік: кожна буква переходить в один і той же знак, де б ця буква не стояла. Для розшифровки таких ходів можна застосувати методи, засновані на підрахунку частот букв. Частіше за всіх букв в тексті зустрічається буква «О», рідше - буква «Ф». Якщо підрахувати для кожного знака частоту, з якою він зустрічається, то можна судити, що цей знак означає. Наприклад, знак, що попадається найчастіше, має багато шансів виявитися пропуском або буквою «О». Можна вивчати і комбінації сусідніх знаків - найчастіше поруч з голосною буквою стоїть приголосна. Навіть не в надто довгому тексті можна без праці відокремити знаки для приголосних букв від знаків для голосних. Такі міркування полегшують розгадку кодів, заснованих на простій заміні букв знаками. Щоб ускладнити розгадку, застосовують шифри «по книзі»: числа коду означають номера рядків і букв на певній сторінці деякої книги, причому номер сторінки можна змінювати в залежності від дати складання послання. Не знаючи, яка це книга, розкрити таємницю коду дуже важко.

 

2.1. Шифри заміни

 Математичний ребус це завдання, в якому шляхом логічних міркувань потрібно розшифрувати значення кожного символу і відновити числовий запис виразу. При цьому однакові цифри шифруються однієї і тієї ж літерою, а різним цифрам відповідають різні літери. Математичний буквений ребус називають крипторифмом, якщо в результаті шифрування отримують певну осмислену фразу

АВ +ВС   СА АВС       19 +98   81 198

Із другого стовпця бачимо, що В+С+А=С, тоді сума В+А повинна закінчуватися на 0. Припустимо А=1, тоді В=9. Отримаємо: 19                    +9С                      С1                    19С   Тепер із першого стовпця знаходимо С: сума 1+9+С+1 десяток (із другого стовпчика) повинна закінчуватися на 9. Очевидно, що це 8.

Шифр Цезаря - один з найдавніших шифрів. При шифруванні кожен символ замінюється іншим, віддаленим від нього в алфавіті на фіксоване число позицій. Шифр Цезаря можна класифікувати як шифр підстановки, при більш вузької класифікації - шифр простої заміни. З точки зору математики шифр Цезаря є окремим випадком афінного шифру. Шифр названий на честь римського імператора Гая Юлія Цезаря, який використав його для секретної переписки.

Початкова абетка: А  Б  В  Г Ґ  Д  Е  Є  Ж  З  И  І  Ї  Й  К  Л  М  Н  О  П  Р  С  Т  У  Ф  Х  Ц  Ч  Ш  Щ  Ь  Ю  Я

Число здвигу - 3

Вихідна : Г Ґ  Д  Е  Є  Ж  З  И  І  Ї  Й  К  Л  М  Н  О  П  Р  С  Т  У  Ф  Х  Ц  Ч  Ш  Щ  Ь  Ю  Я А  Б  В

Мал.2.1. Схема шифру Цезаря.

Ключ : КРИПТОГРАФІЯ

Оригінал тексту : З широким поширенням писемності криптографія стала формуватися як самостійна наука.

Зашифрований текст :  Ш  луіяххй еюзбюскьях еуїрчялбтр аааааааааааа жвфшї іюіьбоьвиьт пч жкєвяджцни гкшї.

 

 

 

2.2. Цифрові і табличні шифри

Алфавіт розбивається на групи з рівним числом букв, потім кожній групі присвоюється свій номер. Так формується перша цифра для шифровки символу. Друга цифра - це порядковий номер букви в групі.

Таблиця 2.1

Цифровий шифр.

АБВГ	ДЕЄЖ	ЗИІЇ	ЙКЛМ	НОПР	СТУФ	ХЦЧШ	ЩЬЮЯ
1	2	3	4	5	6	7	8

Зашифруємо слово «інформація» 33 51 64 52 54 44 11 72 33 84

Таблиця 2.2

Цифрова таблиця.

	1	2	3	4	5	6	7	8	9
1	А	Б	В	Г	Д	Е	Ж	З	І
2	И	Й	К	Л	М	Н	О	П	Р
3	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ
4	Ь	Є	Ю	Я	1	2	3	4	5
5	6	7	8	9	0	+	-	=	!
6	?	(	)	:	;	№	,	.	%

 

Зашифруємо за допомогою цієї таблиці слово «криптографія».

Кожен символ буде зашифровуватися двома цифрами – номером стовпця та номером рядка.  32 92 11 82 23 72 41 92 11 43 91 44

 

 

 

 

 

 

2.3. Шифри перестановки.

При такому способі шифрування змінюється лише порядок слідування символів у вихідному тексті, але не змінюються самі символи. Існує декілька різновидів шифрів перестановки. Використовувався ще за часів Стародавньої Спарти. Для шифровки використовувався жезл «Скітала»  - циліндр, на який намотувалася вузька пергаментна стрічка. На цій стрічці уздовж осі циліндра записувався зашифрований текст. Щоб прочитати цей текст використовувалися циліндри такого ж діаметру.

Таблиця 2.3. Шифр вертикальної перестановки.

5	2	3	4	1
ш	и	ф	р	в
е	р	т	и	к
а	л	ь	н	о
ї	п	е	р	е
с	т	а	н	о
в	к	и	-	-

В шифрі вертикальної перестановки для шифрування використовується прямокутник, в нього вписується текст (зліва направо). Кожен стовпець прямокутника нумерується і потім букви по вертикалі (зверху вниз) виписується згідно нумерації (ключу).

Зашифруємо текст «шифр вертикальної перестановки». Ключ у нас буде цифри 5; 2; 3; 4; 1.

Запишемо послідовно літери із кожного стовпця відповідно до ключа.

Зашифрований текст: вкоео ирлптк фтьеаи ринрн шеаїсв

 

 

 

 

2.4. Матричні шифри

Таблиця 2.4

Схема матричного шифру

А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й	К	Л	М	Н	О	П
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Р	С	Т	У	Ф	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я	«
18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34

Зашифруємо слово «ключ». Запишемо з послідовності літер матрицю

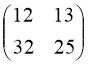  Кодуючу матрицю  я придумала свою:          

Правила множення матриць в загальному вигляді:

Зашифруємо відповідно до правила:

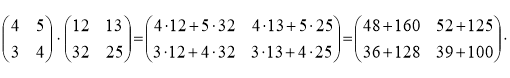
Зашифрований текст: 208;177;164;139

або більш складний варіант без розділових знаків: 208177164139

При отриманні потрібно розшифрувати:

Отримаємо матрицю:

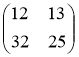
Числа 12; 13; 32; 25 будуть означати слово «ключ»

Таким чином, треба складати фрази з числом букв, кратним 4, щоб легко складати матриці, і знати кодуючу і декодуючу матриці, а також правило множення матриць. Добуток  кодуючої і декодуючої матриці має дорівнювати одиничній  матриці.

2.5. Арифметика остач.

Розділимо кільце на 35 рівних частин, пронумеруємо їх і запишемо  в кожну літеру або знак пунктуації. Номера літер будемо множити на

.Мал.2.2. Схема шифру остач.

Зашифруемо слово «Шифр»: Ш-25 ;И-9;  Ф-21; Р-17

25*2:35=1(ост.15) - О

9*2:35=0(ост.18) - С

21*2:35=1(ост. 7) - Ж

17*2:35=1(ост. 34) – ,  Вихідний текст - «ОСЖ , »

До початку 20-го століття, процес шифрування, в основному, був пов'язаний з лінгвістичними схемами. Зараз інтенсивно використовується математичний апарат, включно з теорією інформації, статистикою, комбінаторикою, алгеброю та теорією чисел.

 

 

2.6. Виконання  обчислень для шифрування та дешифрування за допомогою EXCEL

Додаток Excel виконує цілий ряд обчислень, пов'язаних з матричними даними. Програма обробляє їх, як діапазон комірок, застосовуючи до них формули масиву. Одне з таких дій - це знаходження оберненої матриці. Давайте з'ясуємо, що являє собою алгоритм даної процедури.

Виконання розрахунків

Обчислення оберненої матриці в Excel можливо тільки в тому випадку, якщо первинна матриця є квадратною, тобто кількість рядків і стовпців в ній збігається. Крім того, її визначник не повинен дорівнювати нулю. Для обчислення застосовується функція масиву МОБР. На простому прикладі розглянемо подібне обчислення.

Розрахунок визначника

 Перш за все, обчислимо визначник, щоб зрозуміти, має первинний діапазон зворотну матрицю чи ні. Це значення розраховується за допомогою функції МОПРЕД.

1. Виділяємо будь-яку вільну позицію на аркуші, куди будуть виводитися результати обчислень. Тиснемо на кнопку «Вставити функцію», розміщену близько рядки формул.

 2. Запускається Майстер функцій. У переліку записів, який він представляє, шукаємо «МОПРЕД», виділяємо цей елемент і тиснемо на кнопку «OK».

3. Відкривається вікно аргументів. Ставимо курсор в поле «Масив». Виділяємо весь діапазон комірок, в якому розташована матриця. Після того, як його адресу з'явився в поле, тиснемо на кнопку «OK».

4. Програма проводить розрахунок визначника. Як бачимо, для нашого конкретного випадку він дорівнює - 59, тобто не тотожний нулю. Це дозволяє сказати, що у даній матриці існує зворотна.

Розрахунок зворотної матриці

Тепер можна приступити до безпосереднього розрахунку оберненої матриці.

1. Виділяємо комірку, яка повинна стати верхній лівій осередком оберненої матриці. Переходимо в Майстер функцій, клікнувши по значку зліва від рядка формул.

2. У списку вибираємо функцію МОБР. Тиснемо на кнопку «OK».
3. В поле «Масив», вікна аргументів функції, встановлюємо курсор. Виділяємо весь первинний діапазон. Після появи його адреси в поле, тиснемо на кнопку «OK».

4.Як бачимо, з'явилося значення тільки в одній комірці, в якій була формула. Але нам потрібна повноцінна зворотна функція, тому слід скопіювати формулу в інші комірки. Виділяємо діапазон, рівнозначний по горизонталі і вертикалі вихідного масиву даних. Тиснемо на функціональну клавішу F2, а потім набираємо комбінацію Ctrl + Shift + Enter. Саме остання комбінація призначена для обробки масивів.

Як бачимо, після цих дій зворотна матриця обчислена в виділених осередках.

Процедура множення матриць

Відразу потрібно сказати, що перемножити між собою можна далеко не все матриці, а тільки ті, які відповідають певній умові: число стовпців однієї матриці має дорівнювати кількості держав рядків інший і навпаки. Крім того, виключається наявність в складі матриць порожніх елементів. У цьому випадку теж виконати необхідну операцію не вийде. Застосування функції МУМНОЖ відноситься до математичної групі функцій. Якраз його безпосереднім завданням і є знаходження добутку двох матричних масивів. Синтаксис МУМНОЖ має такий вигляд:=МУМНОЖ(массив1;массив2)

Таким чином цей оператор має два аргументи, які представляють собою посилання на діапазони двох перемножуєте матриць.

Тепер давайте подивимося, як використовується функція МУМНОЖ на конкретному прикладі. Є дві матриці, число рядків однієї з яких, відповідає кількості стовпців в інший і навпаки. Нам потрібно перемножити два цих елементу.

Виділяємо діапазон, де буде відображатися результат множення, починаючи з його верхньої лівої комірки. Розмір даного діапазону повинен відповідати числу рядків у першій матриці і числу стовпців у другій. Клацають по піктограмі «Вставити функцію».

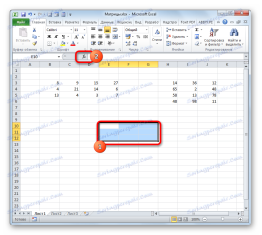
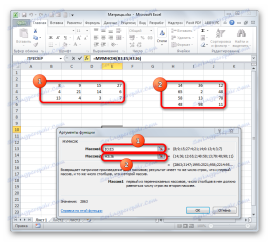
Активується Майстер функцій. Подорожуємо у блок «Математичні», натискаємо по найменуванню «МУМНОЖ» і клацають по кнопці «OK» в нижній частині вікна.

Як бачимо, після цього попередньо виділений діапазон був заповнений даними. Це і є результат множення матричних масивів. Якщо поглянути на рядок формул, після виділення будь-якого з елементів даного діапазону, то ми побачимо, що сама формула обгорнута в фігурні дужки. Це і є ознака функції масиву, який додається після натискання клавіш Ctrl + Shift + Enter перед виведенням результат на лист.

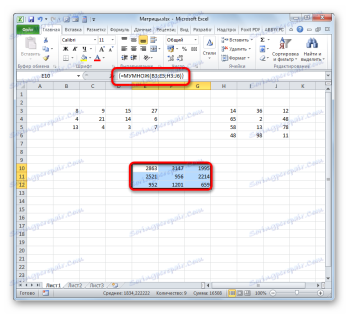
Як бачимо, якщо  робити розрахунок визначника і оберненої матриці , множення матриць  тільки за допомогою ручки і паперу, то над цим обчисленням, в разі роботи над складним прикладом, можна ламати голову дуже довго. Але, як бачимо, в програмі   EXCEL дані обчислення проводяться дуже швидко, незалежно від складності поставленого завдання. Для людини, яка знайома з алгоритмом подібних розрахунків в цьому додатку, всі обчислення зводиться до чисто механічних дій.

 

2.7.Розробка завдань для формування практичних навичок

шифрування

В 8 класі вивчається тема уроку з інформатики «Опрацювання даних як інформаційний процес. Кодування та декодування повідомлень». Метою вивчення шифрування інформації в школі є формування комплексу знань, на яких базуються сучасні методи криптографії та набуття практичних навичок у реалізації цих методів, формування понять: кодування даних, декодування даних, передавач, приймач, канал зв'язку; формування вміння користуватися готовими системами кодування та розробка власних систем кодування. Тому нами було розроблено завдання до  практичних занять  для  шифрування даних на уроках.

ДОДАТОК А Практична робота «Опрацювання даних як інформаційний  процес. Кодування та декодування  повідомлень» 

ДОДАТОК Б Практичне заняття захисту інформації за допомогою криптографічних алгоритмів.

 

ВИСНОВКИ

 

Сучасне суспільство все більшою мірою стає інформаційним, успіх будь-якого виду діяльності все сильніше залежить від володіння певними відомостями і від відсутності їх у конкурентів. Інформацію зберігають, транспортують, продають і купують, а значить - крадуть і підробляють - і, отже, її необхідно захищати. Серед всього спектру методів захисту даних від небажаного доступу особливе місце займає шифрування.

 Під шифром розуміється сукупність оборотних перетворень заснованих на математичних методах. Найважливіші складові будь-якого шифру - це загальні правила, за яким перетворюється вихідний текст.

 Вивчивши та проаналізувавши літературу та Internet ресурси з теми «Шифрування» я дійшла висновку, що на сучасному етапі процес шифрування тісно пов'язаний з математикою, на відміну від стародавніх процесів шифрування, що були в основному лінгвістичними. Історія захисту інформації починається, цілком імовірно, десь у той час, коли люди почали вчитися спілкуватися за допомогою переписки. Природно, їм потрібні були способи забезпечити її таємність. Точних дат і достовірних даних про тайнопис у стародавності ніхто не приводить. Відомо, наприклад, що в Древній Греції голову раба голили, писали на його голові, чекали, коли волосся знову виростуть, після чого відправляли з дорученням до адресата. Методи ці розвивалися й ускладнювалися разом із ходом технічного прогресу. Вершиною розвитку цих методів можна вважати, імовірно, технологію створення мініатюрних фотографій - так званих точок, - які з'явилися після Другої світової війни. Така точка розміром із крапку друкованого тексту могла містити сотні документів.  Бурхливий розвиток комп'ютерних технологій і мереж, кардинально змінили сучасне суспільство. В даний час засоби електронної пошти, електронного документообігу, штрихування товарів та шифрування медичної інформації використовуються в повсякденному житті і тому вимагають застосування додаткових засобів для забезпечення конфіденційності, контролю доступу, цілісності та ідентифікації.

В роботі я розглянула застосування математичних методів в процесі шифрування і дешифрування: арифметику остач, методи заміни та перестановки, метод шифрування за допомогою матриць і виконала  обчислення для шифрування та дешифрування за допомогою EXCEL.  Виконали розробку завдань для формування практичних навичок шифрування  та застосували на уроках інформатики математичні методи шифрування інформації.

 Таким чином, можна стверджувати, що процес шифрування, самий надійний спосіб захисту інформації, в сучасному суспільстві відбувається за допомогою математичних методів.

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.               Алфьоров А.П., Зубов А.Ю., Кузьмин А.С., Черьомушкин А.В. Основи  криптографії. - М.: Геліос, 2005.
2.               Баричев С.Г., Гончаров В.В., Сєров Р.Е. Основи  сучасної криптографії. - М.: Гаряча лінія  - Телеком, 2002.
3.               Виленкин Н.Я. Математика и шифры. «Квант».№7.1977. С.52-56
4.               Жельніков В.К.  Криптографія від папірусу до комп’ютера. - М.:ABF, 1996.
5.               Зельманзон, М., Хлобыстова, Л. Самосовмещение квадрата и тайнопись  «Квант», № 12, 1980. С. 32-34.
6.               Дориченко С.А.,  Ященко В.В. 25 этюдов о шифрах. –М.:ТЕИС, 1994.
7.               Коробейников А. Г. Математические основы криптографии. Учебное пособие. СПб: СПб ГИТМО (ТУ), 2002.
8.               Коробова, Л. Математические загадки детективного сюжета «Математика» // Прил. к газете «Первое сентября», №19,1998 г.
9.               Ященко В. В. Основные понятия криптографии // Математическое просвещение. Сер. 3. №2. 1998. С. 53-70.

10.     Мачула В. Г. Excel 2007 на практике: — Санкт-Петербург, Феникс,

2009 г.- 160 с.

Internet – ресурси.

1.               http://www.fidel-kastro.ru/crypto/zhelnik.htm
2.               http://www.uran.donetsk.ua/~masters/2005/feht/chernenkaya/ind/history.htm
3.               http://persona.rin.ru/view/fall//31397/polibij-polybios
4.               http://www.tonnel.ru/?l=kniga&273
5.               http://www.c-cafe.ru/days/bio/5/085.php
6.               http://persona.rin.ru/view/f/0/35276/shennon-klod-elvud
7.               http://www.enlight.ru/crypto/articles/shannon/__shann.htm