СИСТЕМА РОЗВ’ЯЗУВАННЯ ТВОРЧИХ ЗАВДАНЬ НА УРОКАХ МАТЕМАТИКИ (методичні рекомендації)

 

 

СИСТЕМА РОЗВ’ЯЗУВАННЯ  ТВОРЧИХ  ЗАВДАНЬ  НА  УРОКАХ  МАТЕМАТИКИ

(методичні рекомендації)

 

 

 

 

 

 

Система розв’язування творчих  завдань  на уроках математики. Методичні  рекомендації. Заклад  загальної середньої освіти ….

 

У  посібнику  розкрито  основні  засади  розв’язування творчих  завдань  на  уроках  математики  в   закладах  загальної  середньої  освіти. 

У першому розділі висвітлено зміст та принципи технології  розв’язування  винахідницьких  задач (ТВРЗ)  та  особливостей  її  застосування на  уроках  математики  з  метою  творчого  розвитку  учнів.

У другому розділі надано методичні рекомендації щодо використання системи розв’язування творчих  завдань  на уроках математики,  наведено  приклади  розв’язування  нестандартних  задач  різними способами, що  спрямовані  на поглиблен­ня та систематизацію знань  учнів із розв’язування нестандартних математичних задач, формування  вмінь розв’язувати такі задачі,  знаходити  раціональні  способи  обчислення.

Творчі  нестандартні  задачі  формують  стійкий   пізнавальний  математичний  інтерес, розвивають логічне й креативне мислення учнів, просторову  уяву, творчі  здібності та можуть використовуватися педагогами на різних етапах уроку.

Рекомендовано  вчителям  математики закладів середньої  освіти.

Автор:

????,  вчитель  математики ????.

Рецензент:

,,,,, вчитель-методист

Навчально-методичне видання затверджено методичною радою  ЄЄЄЄ

Протокол  № 2  від  Є.01.20  року.

ЗМІСТ

 

ВСТУП……………………………………………………………………………….3

Розділ  1. ТЕОРЕТИЧНІ ЗАСАДИ ВИКОРИСТАННЯ СИСТЕМИ  РОЗВ’ЯЗУВАННЯ  ТВОРЧИХ  ЗАВДАНЬ  НА  УРОКАХ  МАТЕМАТИКИ…………………………………………………………………….6

1.           Технологія  розв’язування творчих  завдань як  засіб розвитку учнів  на уроках математики…………………………………………………….6
2.           Використання  творчих  завдань  на  уроках  математики....................10

Розділ 2. МЕТОДИЧНІ ОСОБЛИВОСТІ ВИКОРИСТАННЯ  СИСТЕМИ РОЗВ’ЯЗУВАННЯ  ТВОРЧИХ  ЗАВДАНЬ  НА  УРОКАХ  МАТЕМАТИКИ…………………………………………………………………...14

1. Практичний досвід використання системи розв’язування творчих завдань на уроках математики ……………………………………………………...14
2. Методичні рекомендації щодо розв’язування творчих завдань у процесі вивчення математики……………………………………………………….25

ВИСНОВКИ………………………………………………………………………..30

СПИСОК  ВИКОРИСТАНОЇ  ЛІТЕРАТУРИ…………………………….......32

ДОДАТКИ………………………………………………………………………….34

 

 

ВСТУП

 

Головною  метою  освітньої  галузі  «Математика» Державного  стандарту базової  і  повної  загальної  середньої освіти  є формування в учнів математичної компетентності на рівні, достатньому для забезпечення життєдіяльності в сучасному світі, успішного оволодіння знаннями з інших освітніх галузей у  процесі шкільного навчання. Згідно з Державним стандартом  сучасний  учень  повинен  володіти  не  тільки  певним  набором знань, вмінь та навичок але  й  вміти критично та творчо мислити, чітко й аргументовано  формувати  і  висловлювати   свої  судження.

Отже, сучасна освіта  має бути зорієнтована на особистісний розвиток кожного учня відповідно до його здібностей.

Сьогодні спостерігається загальне зниження зацікавленості та бажання учнів  вивчати  дисципліни  математичного циклу. Це негативно відбивається на якості  знань і  умінь учнів, їх  інтелектуальному  розвиткові. Питання  про те, яким чином зробити важкі та не завжди зрозумілі математичні знання цікавими й  доступними для учнів, яким  чином сприяти отриманню учнями того необхідного багажу знань, який стане підґрунтям розвитку творчого пошуку  школярів, і  в той же час  не  перетворити  освітній  процес  на  розвагу,  є  актуальним  чи  не  для  кожного  вчителя  математики.

Враховуючи  зазначені  вище  проблеми, дуже актуальним є питання щодо створення та широкого впровадження в повсякденну педагогічну практику інноваційних технологій, що покликані забезпечити подальше вдосконалення навчально-виховного процесу, доступність та ефективність освіти,  підготовку  учнів  до  життєдіяльності  в  інформаційному  суспільстві.

Однією з інноваційних освітніх технологій є система  розв’язування творчих завдань, більш  відома  як   теорія  розв'язування  винахідницьких  задач (далі – ТРВЗ).

Технологія ТРВЗ – це інструмент для розвитку творчого мислення дорослих і  дітей. Основою  зазначеної технології є роботи  Г.С. Альтшуллєра «Алгоритми  винаходу» (1969)  та  «Творчiсть  як  точна  наука» (1979).

Основною ідеєю ТРВЗ є творчість в усьому  в постановці запитань; в  прийомах  їх  розв'язання;  в  подачі  матеріалу.

Система  ТРВЗ  давно  зацiкавила  педагогiв i психологiв, якi адаптували її для роботи з дiтьми спочатку в школi, а потiм i в дитячому садку. Згодом з’явилися спецiальнi  дослiдження (В. А. Бухвалов, Б.Л. Злотiн, Г.І. Іванов,  С.М. Ладошкiна, А.О. Нестеренко, Т.М. Сидорчук,  Л.I.Шрагiна, М.Н. Шустерман), в яких  була розроблена  серiя  методiв  та  прийомiв  навчання  школярiв   на  базi   технології  розв’язування  винахідницьких  задач.

На сьогодні  розроблений комплекс вправ на основі ТРВЗ, до складу якого входять методи і прийоми, що розвивають творче мислення і його основний компонент  уяву. Основні функції й галузі застосування ТРВЗ в освітньому процесі: рішення винахідницьких (нестандартних, творчих) задач будь-якої складності й спрямованості; розвиток творчої уяви і мислення; розвиток  якостей  творчої  особистості   й  розвиток  творчих  колективів.

Система розв’язування творчих завдань на уроках математики вчить мислити логічно, творчо, допомагає  розбудити в  дитині  креативну особистість, активізувати її творчий потенціал. Використання ТВРЗ надає педагогам можливість активізувати навчально-пізнавальну діяльність учнів, підвищити  рівень їхньої математичної  грамотності,  збільшити  роль  самостійної  роботи  на  уроках. 

Розділ  1

ТЕОРЕТИЧНІ ЗАСАДИ ВИКОРИСТАННЯ СИСТЕМИ РОЗВ’ЯЗУВАННЯ  ТВОРЧИХ  ЗАВДАНЬ НА УРОКАХ МАТЕМАТИКИ

 

1.          Технологія розв’язування творчих завдань як засіб розвитку  учнів  на  уроках  математики

 

Останнiм часом як головне концептуальне питання педагогiки постала проблема формування творчої особистостi. Інтенсивне прискорення науково-технічного прогресу, невпинне зростання інформації про світ і необхідність оволодіти нею поставили перед педагогами і психологами ряд складних завдань. Сьогодні у всіх галузях суспільства потрібні такі спеціалісти, які б не тільки  досконало володіли фахом, спеціальністю, але й уміли працювати творчо. Відтак  проблема  творчих здібностей переросла у соціальну. Знання все швидше починають «старіти», «відмирають» одні професії і «народжуються» інші.  Частка  розумової  праці  постійно  зростає.

Отже, творчі здібності людини слід визнати найістотнішою складовою її інтелекту, а завдання їх розвитку  одним із найважливіших у педагогічній роботі. В.О.Сухомлинський писав: «Духовне життя дитини повноцінне лише тоді, коли  вона живе  у світі гри, казки, музики, фантазії, творчості. Ми повинні вчити і виховувати так, щоб дитина почувала себе шукачем і відкривачем знань. Тільки за цієї умови одноманітна, напружена, стомлююча робота школяра забарвлюється радісними почуттями і може принести маленьким  людям  переживання  творця» [21, с.56].

Дійсно, вчителям необхідно зацікавлювати учнів математикою, розвивати їх здібності і творчий потенціал. Коли йдеться про зміст шкільного курсу математики, то, звичайно, мають на увазі засвоєння учнями певної системи математичних знань, умінь і навичок. Але не можна зводити все математичне навчання в школі до передачі учням визначеної суми знань і навичок. Це обмежувало б роль математики в загальній освіті. Тим більше в наш час, коли математика рухається до нових ідей, що виходять за межі стандартних теоретико-множинних уявлень, стає очевидною організаційна роль інноваційних педагогічних технологій в розвитку математики як різновиду наукової творчості. Елементи технології розв’язання винахідницьких задач (ТРВЗ)  можуть  бути  ґрунтовним  фундаментом  у  вирішенні  цієї  проблеми. 

Довгий  час єдиним інструментом розв’язання творчих завдань  задач, які  не  мають  ефективних механізмів розв’язання,  був метод спроб і помилок.  Г.С.Альтшуллер, який створив «Теорію розв’язання винахідницьких задач» поставив  ціль інакше: «як без довгого перебирання варіантів розв’язання  завдання  виходити  відразу на сильне вирішення?».  Розв’язати цю дилему  дозволяють  принципи, які  лежать  в  основі  технології  ТРВЗ (рис.1.)

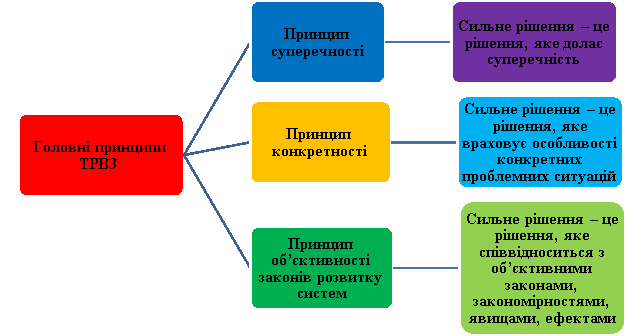
Рис.1. Принципи  технології  розв’язання  винахідницьких  завдань

 

Оновлення дидактичної системи на уроках математики, творчого розвитку учнів за теорiєю розв’язання винахiдницьких завдань залишається актуальним і сьогодні. І хоча ТРВЗ  як наукова технологiя виникла в технiцi, але практика засвiдчила, що iдеї ТРВЗ можуть бути використанi в педагогiцi. Створена ще в 1996р. в м. Рiвне украiнська лабораторiя педагогiки ТРВЗ пiдтвердила факт, що ТРВЗ вiдповiдає на одне з головних питань дидактики – як дiтей навчати творчостi, за допомогою яких вправ, прийомiв. Крiм того, ця технологiя сприяє оволодiнню учнями методами пошуку нової генерацiї оригiнальних  iдей, розвитку  фантазiї, мислення.

Головна iдея теорiї Г.С.Альтшуллєра  полягає в тому, що технiчнi рiшення виникають i розвиваються  не стихiйно, а за певними законами, які можна пiзнати та використати для розв’язання винахiдницьких завдань.

Психолог Л.О.Макрiдiна видiляє такi концептуальнi положення технологiї ТРВЗ:

• Теорiя – каталiзатор  творчого  розв’язання  проблем.
• Знання – iнструмент, основа  творчої  iнтуiцiї.
• Творчими  здiбностями  надiлена  кожна людина (винаходити можуть всi).
• Творчості,  як i  будь-якiй  дiяльностi, можна  навчитися [15, с.14].

Технологiя ТРВЗ вiдрiзняється вiд iнших методик тим, що це не поєднання окремих прийомiв, а технологiя, завдяки якiй можна вирiшувати рiзнi складнi проблеми, задачi, бути в постiйному творчому пошуку.

Технологiя ТРВЗ володiє широким арсеналом методiв, якi розвивають пiзнавальнi та творчi здiбностi дiтей: вмiння встановлювати причинно-наслiдковi зв’язки, робити висновки, iнтегрувати й синтезувати iнформацiю, аналiзувати ситуацiї, передбачати наслiдки, будувати гiпотези, застосовувати новi iдеї та методи розв’язання задач на практицi; здатнiсть висловлювати оригiнальнi iдеї i винаходити щось нове. За допомогою ТРВЗ створено принцип, завдяки  якому педагог разом з учнями може знаходити логiчний вихiд з  будь-якої  ситуацiї, а  учень – грамотно  вирiшувати  свої  проблеми.

ТРВЗ – це не лише система для розв’язування творчих завдань, а й система виховання та розвитку мислення людини. Головне мiсце в нiй займає життєва  стратегiя  творчої  особистостi  та  розвиток  творчої  уяви.

Мета ТРВЗ – не просто розвинути фантазiю дiтей, а навчити їх мислити системно, з розумiнням процесiв, якi вiдбуваються, дати в руки вчителя iнструмент для конкретного практичного виховання у дiтей якостей творчої особистостi, здатної розумiти єднiсть i протирiччя навколишнього свiту, ставити i вирiшувати проблеми.

Уроки математики з використанням технології розв’язування творчих завдань вчать учнів виявляти суперечливi властивостi предметiв, явищ i розв’язувати цi протирiччя. Виявлення та розв’язання протирiч – ключ до творчого мислення. Але головне завдання: навчити учнів шукати i знаходити свої рiшення, бути винахiдливими, що виявляється у творчiй фантазiї, мiркуваннi,  придумуваннi  чогось  нового.

Відтак технологія ТВРЗ  змушує  до побудови освітнього процесу, у якому  вчитель та  учні перебувають у постійному творчому пошуку, вирішують  складні проблеми, задачі. Методи, які застосовують у  даній технології, розвивають такі пізнавальні та творчі здібності, як уміння робити висновки, оперувати інформацію, аналізувати ситуації, передбачати наслідки; здатність винаходити нові оригінальні ідеї, знаходити кілька правильних відповідей  та  ін.

Роль учителя за ТРВЗ полягає у вмінні  раціонально  розподілити час на уроці,  цікавому підборі завдань, прагненні навчити учнів творчості, адже відомо, що творчості як і будь якій діяльності можна навчитися.

Отже, ТРВЗ забезпечує розв’язання задач на основi логiчних операцiй, алгоритмiв замiсть порожнiх спроб i пошукiв наослiп. Відтак технологiя ТРВЗ – це новий iнструмент для розвитку творчого мислення дорослих i дiтей.

Головнi принципи ТРВЗ:

• усування суперечностей;
• системний пiдхiд (вмiння бачити навколишнiй свiт у взаємозв’язку всiх його елементiв);
• вмiння знайти необхiдний у данiй ситуацiї спосіб розв’язання.

 

 

1.2. Використання  творчих  завдань  на  уроках  математики

 

Математика як навчальний предмет надає широкі можливості для здійснення процесу формування та розвитку оперативності мислення учнів. Використання  системи розв’язування творчих завдань (нестандартних завдань підвищеного рівня складності) дає можливість педагогу вчити школярів  міркувати, творити, шукати, узагальнювати, порівнювати. У такому аспекті уроки  математики  можна  розглядати  як  різновид  наукової  творчості.

Стан математичної підготовки учнів у першу чергу характеризується вмінням розв’язувати задачі. Видатний методист і математик Д.Пойа писав: «Що значить оволодіння математикою? Це є вміння розв’язувати задачі. Причому не тільки стандартні, але й ті, що вимагають відомої незалежності мислення, здорового  глузду, оригінальності,  винахідливості» [19, с. 9].

Як відомо, навчальні математичні задачі можна умовно поділити на стандартні й нестандартні (творчі). Задачу вважають стандартною, якщо її розв’язання вимагає від учнів застосувати певний відомий їм алгоритм чи скористатися зразком. Нестандартною (творчою) називають задачу, алгоритм розв’язку  якої наперед невідомий. Щоб виконати таку задачу, треба, як зазначає Б.Г. Друзь, «всебічно врахувати взаємозв’язки між даним і шуканим, правильно оцінити окремі компоненти завдання, поданого у нестандартній формі, зрозуміти властивості величин та залежності між ними, які безпосередньо не зазначені в умові, але випливають з певних закономірностей, причинних або функціональних залежностей» [9, с. 13].

Творчі (нестандартні) задачі  характеризуються відкритістю, невизначеністю і мають такі особливості: наявність потреби у багатократній зміні підходів до розв’язування; необхідність у створенні значної кількості варіантів розв’язування, спрямованість учня на знаходження особливих, часто неочікуваних результатів; прогнозування кількох правильних альтернативних розв’язань.

Для  розв’язування  нестандартної  задачі учень  не  має готової схеми дій, або  задачу неможливо розв’язати відомими способами, до результату також  неможливо  перейти  на основі  прямого  відтворення  знань і операцій.

Отже, нестандартні задачі – це такі, для яких в курсі математики немає загальних  правил і  положень, що визначають точну програму їх розв’язування.

На уроках математики,  розв’язуючи різні  види  творчих завдань (задач), учні  розширюють і поглиблюють набуті на уроках знання.

Б.Г.Друзь  визначає  такі  групи  творчих  завдань    уроках  математики:

1. Завдання, пов’язані з важливими поняттями і методами математики (вправи на використання елементів теорії множин та поняття відношення, задачі комбінаторного та ймовірнісного характеру, вправи на формування найпростіших топологічних уявлень, логічні задачі, цікаві вправи, пов’язані з ідеєю «обчислювальної  машини»).

2. Завдання з елементами дослідження. Це, зокрема, вправи із словами: порівняйте, виділіть головне, покажіть, обґрунтуйте, доведіть, узагальніть тощо.

3. Завдання на відкриття «нових» зв’язків, залежностей, закономірностей (управи на здійснення простих умовиводів, класифікацій та групувань предметів).

4. Практичні завдання і вправи (вправи на використання різних тверджень; оптимізаційні  задачі; вправи  політехнічного  спрямування; графічні вправи-діаграми, таблиці; шкали, схеми, графіки; вправи геометричного  змісту, вправи  на  маніпулювання  із  предметами).

5. Самостійно складені учнями вправи спочатку за аналогією, пізніше  за даною  умовою.

6. Вправи на кмітливість, в яких вимагається розв’язувати приклади різними способами, записувати  числа  кількома даними цифрами, відновлювати у прикладі пропущений знак або цифру, знаходити помилку в розв’язанні тощо. Це завдання з логічним навантаженням, математичні ребуси, кросворди.

7. Цікаві вправи та ігри (вправи, які вражають швидкістю і легкістю обчислень, оригінальними і часом несподіваними результатами; логічні ігри, задачі-вірші, задачі-казки, задачі-загадки, задачі-жарти тощо.) [8, с.21].

Такі творчі завдання сприяють розвитку інтересу до математики. При підборі  творчих завдань та пізнавального матеріалу вчитель повинен дбати про їх доступність. Треба уникати надто складних завдань, щоб перед учнями не поставали непереборні труднощі, оскільки це негативно впливає на становлення пізнавального  інтересу дітей. Уводячи позапрограмний  матеріал, учитель  повинен  керуватися  принципом  наступності.

Оскільки мова йде про нестандартні вправи для розвитку творчого мислення, то для пожвавлення й підтримання інтересу школярів до завдань, останні повинні задовольняти наступним умовам:

• бути  несхожими  на  завдання, запропоновані  у  підручнику;
• зміст завдань повинен бути зрозумілим учням;
• види, послідовність і кількість вправ повинні бути взаємопов’язані; відповідати темі та віковим особливостям учнів;
• завдання повинні викликати інтерес;
• дії  учнів  слід  контролювати,  своєчасно виправляти та спрямовувати;
• завдання  урізноманітнювати, не  пропонувати  однотипні;
• вправи  не  пропонувати  стихійно, а  використовувати  систематично;
• творчі завдання та цікаві питання можна пропонувати на етапі закріплення знань, умінь і навичок;
• задачі з логічним навантаженням варто розв’язувати з усім класом;
• творчі завдання варто супроводжувати унаочненням та використовувати їх під час засвоєння, поглиблення, систематизації знань учнів [14, с. 29].

Тільки за таких умов можна досягти високої якості кінцевих результатів, запобігти відставанню слабко встигаючих і забезпечити розвиток творчого мислення усіх учнів відповідно до їх навчальних можливостей.

Завдання не повинні бути дуже легкими, але і не дуже важкими, оскільки учні, не розв’язавши задачу або не розібравшись в розв’язанні, запропонованому  вчителем, можуть  втратити не  лише інтерес до предмету, а й взагалі віру в свої сили (в цьому випадку дуже важливо підтримати, допомогти). Перш за все, вчитель не повинен знайомити учнів з вже готовим розв’язанням. Підказка  повинна бути мінімальною. Важливо показати дітям, що від  розв’язання математичної задачі можна отримати таке ж задоволення, як від розгаданого кросворду або ребусу.

Щоб допомогти учню знайти шлях до розв’язання задачі, вчитель повинен уміти поставити себе на його місце, спробувати побачити і зрозуміти джерело його можливих ускладнень. Уміла допомога вчителя залишить частку самостійної роботи, дозволить учням розвинути математичні здібності, накопичити свій досвід, який надалі допоможе знаходити шлях розв’язання нових завдань. Тобто краще, що може зробити вчитель для учня, полягає в тому, щоб шляхом ненастирливої допомоги підказати йому блискучу ідею. А хороші  ідеї  мають своїм джерелом минулий досвід і  раніше  придбані  знання.

Часто виявляється доречним почати роботу з питання: «Чи відоме вам яке-небудь споріднене завдання?». Уміння підбирати допоміжні завдання свідчить про те, що учні вже володіють певним досвідом розв’язання творчих завдань. Якщо цей досвід невеликий, то можна запропонувати їм допоміжні завдання, які допоможуть зрозуміти ідею розв’язання.

Таким чином, використання творчих вправ урізноманітнює проведення уроків математики. Вміння розв’язувати творчі завдання є основним показником хороших  математичних  знань. Щоб навчитися розв’язувати творчі задачі, необхідно зрозуміти відповідну теорію, а глибоко зрозуміти суть теорії допомагає розв’язування достатньої кількості різноманітних творчих  завдань за  допомогою  ТВРЗ.

 

Розділ 2

МЕТОДИЧНІ ОСОБЛИВОСТІ ВИКОРИСТАННЯ  СИСТЕМИ РОЗВ’ЯЗУВАННЯ ТВОРЧИХ ЗАВДАНЬ НА УРОКАХ МАТЕМАТИКИ

 

2.1. Практичний досвід використання  системи розв’язування творчих  завдань  на  уроках  математики

 

Творчі завдання  це такі, для яких в курсі математики не має загальних правил і положень, що визначають точну програму їх розв’язування.

Процес розв’язування будь-якої творчого (нестандартного)  завдання складається у послідовному застосуванні двох основних операцій:

1.  Зведення (шляхом перетворення або переформулювання) творчої задачі  до  рівносильної їй,  але уже стандартної.
2. Розбиття нестандартної задачі на декілька стандартних підзадач.

В залежності від характеру нестандартної задачі використовуємо або одну із цих операцій, або обидві. При розв'язуванні більш складних задач ці операції доводиться застосовувати багаторазово.

Розглянемо деякі методи розв’язування нестандартних задач (рис.2.)

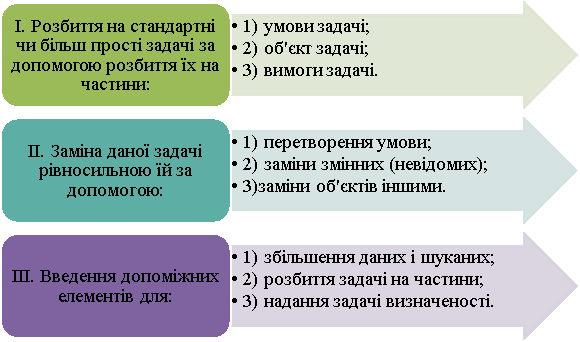
Рис.2.  Методи  розв’язування  творчих  завдань

У  курсі  математики не має загальних правил і положень, що визначають точну програму розв’язування творчих завдань. Математика не займається розробкою таких правил, але в шкільному курсі математики на дуже багатьох прикладах  можна  спостерігати застосування цих операцій.

Для того, щоб ефективно розв’язати творче завдання, потрібно правильно організувати наявну інформацію, зосередитися на ключових моментах, відкидаючи все  другорядне. Деякі завдання вирішуються досить ефективно за допомогою продуманої тактики послідовних кроків. Інші можна вирішити експериментальним  шляхом  методом проб і помилок. Треті здаються тільки після довгого міркування, причому відповідь часто виникає як осяяння. У будь-якому  випадку  доводиться  оперувати  наявною  інформацією.

З практичного досвіду нами помічено, що використання системи розв’язування творчих завдань на уроках математики якнайкраще розвиває у дітей логічне мислення, інтерес до навчання, предмету. Треба лише вдало добирати математичні завдання, щоб вони викликали цікавість у школярів. Адже  пробудити інтерес до математики, навчати школярів творчо мислити  це найголовніша мета, до якої прагне вчитель у зв’язку з завданням підвищення ефективності процесу навчання математики. Цьому сприяють: практичне ознайомлення школярів з нестандартним підходом до розв’язання творчих завдань; вправляння в пошуках оригінальних рішень; багатогранна творча діяльність  школярів, яка  спрямована  на формування навичок пошукової праці. Для вирішення цих завдань використовуємо різноманітні творчі вправи, запитання, цікаві задачі, логічні вправи, задачі-головоломки, задачі-жарти, дидактичні  ігри, загадки, ребуси, які в свою чергу передбачають:

• встановлення суперечності;
• встановлення причинно-наслідкових зв’язків;
• встановлення схожості та різниці між об’єктами, що порівнюються;
• зіставлення  різних варіантів та дії вибору;
• виділення певних закономірностей в навчальній інформації;
• доведення правильності виконаних практичних або розумових дій;
• пошук і виправлення припущених помилок;
• висування гіпотез, пропозицій, здійснення певного прогнозу наступних подій.  Додаток.

Розглянемо деякі  приклади  розв’язування  творчих  завдань на уроці математики.

Приклад 1. Обчисліть найбільш раціональним способом:

arctg 1 + arctg 2 + arctg 3.

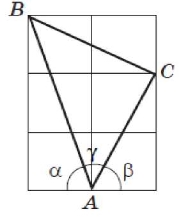Розв’язання. Нова ідея полягає в застосуванні рисунка як графічної моделі  розв’язання  задачі. Тож зробимо рисунок.

За рисунком видно, що tg а = 3, звідки а = arctg 3;

tg β = 2, звідки β = arctg 2.

Трикутник ABC є прямокутним і рівнобедреним, тому tg  γ = tg 45° = 1, звідки γ = arctg 1.

Отже, arctg 1 + arctg 2 + arctg 3 = π [1]

Приклад 2. Потяг проходить відстань від міста А до міста В за 10 год 40 хв. Якби швидкість потяга була на 10 км/год менша, то він прийшов би на 2 год 8 хв пізніше. Знайти відстань між містами та швидкість потяга.

Розв’язання. Розв’яжемо задачу нестандартно  графічно, а не з допомогою  складання  рівняння, як уже всі давно звикли.

По горизонтальній осі будемо відкладати швидкість потяга, а по вертикальній  час. Оскільки відстань, яку пройшов потяг, рівна добутку 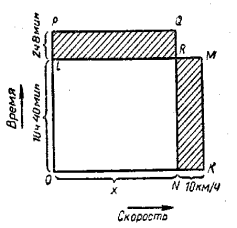швидкості на час, то площа прямокутника, сторони якого відповідно зображають швидкість і час, зобразить відстань, яку пройшов потяг.             

Нехай  відрізок ОК  швидкість поїзда, а відрізок  ОL  час ходу (10 год 40 хв); в такому випадку площа прямокутника OKML зображає відстань між містами А і В. Якщо швидкість потяга зменшиться на 10 км/год (на відрізок KN), то час ходу збільшиться на 2 год 8 хв (на відрізок LP). В цьому випадку відстань АВ зобразиться площею прямокутника ONQP.  Оскільки відстань між містами в обох випадках одна й та ж сама, то площі прямокутників OKML і ONQP мають бути рівними; оскільки прямокутник ONRL  їх спільна частина, то площа прямокутника NKMR має бути рівна площі прямокутника LRQP. Позначивши невідому зменшену швидкість потяга (відрізок ON) через х, отримаємо:

10 год 40 хв  10 = 2 год 8 хв  х  , звідки

х =  10 =  10 = 50

Швидкість потяга: 50+10=60 (км/год).

Відстань між містами: 60 х 10 = 640 км. [4].

У шкільному  курсі математики є творчий матеріал, що може здивувати та заціка­витии школярів. Наприклад, на уроці алгебри при ви­вченні теми «Множення різниці двох виразів на їх суму» можна спочатку провести усний рахунок  під  девізом  «Хто швидше?» (знайти добуток двох чисел 21х19; 31x29; 42x38; 45x35; 201х199). Після  закінчення  усного рахунку слід відмітити, що помножити числа можна швидше, якщо вивчити важливий і цікавий розділ «Формули скороченого множення». Учні 7 класу ще не ознайомлені з розкладанням ква­дратного тричлена на множники за загальною формулою, тому задача розкласти на множники a  2a  3 для них є творчою.

Цікаво, що постав­лена задача може бути розв’язана де­кількома способами. Методично доцільно пояснити це учням так:

1. a² - 2a - 3 = 3a² - 2a² - 2a - 3 = 3(a² -1) - 2a (a + 1) = 3(a - 1) (a +1) - 2a (a +1) = (a + 1) (a - 3).
2. a² - 2a - 3 = a² - 3a + a - 3 = a (a - 3) + (a - 3) = (a – 3)(а+1)
3. a² - 2a - 3 = a² - 2a - 2 -1 = (a² -1) - 2(a + 1) = (a + 1)(a - 3).
4.  a² - 2a - 3 = a² - 2a +1 - 4 = (a-1)² - 2² = (a + 1)(a - 3).

Викликати в учнів інтерес до математики можна й за допомогою нестандартних і доведених прикладів. Крім повідомлення нових фактів, розгляду відомого матеріалу під іншим кутом зору, стимул но­визни може приймати й інші форми. Наприклад, виявлення відомих за­кономірностей у результаті безпосе­редньої дослідницької роботи. Так, на уроці геометрії у 8-у класі перед доведенням теореми Піфагора пропонуємо учням побудувати прямокутний трикутник з катетами а=3 см, в=4 м. Потім виміряти гіпотенузу з точністю до цілих чисел і переві­рити, чи буде виконуватися рівність: а²+в²=с². Учні під керівництвом учи­теля самі формулюють і доводять тео­рему  Піфагора.

Для закріплення мате­ріалу пропонуємо розв’язати задачу: чи існують три послідовних цілих числа, які відподіають теоремі Піфагора? Учні позначають сторони прямо­кутного трикутника n-1, n, n+1 і легко знаходять катети й гіпотенузу. Після використання теореми Піфагора і перетворення виразу (n -1)²+n²=(n+1)² учні отримують n=4. Числа 3, 4, 5 є довжинами сторін прямокутного трикутника. Розповідаємо учням, що на основі даної тео­реми Піфагор створив правило для знаходження цілих чисел, якими представлені довжини сторін прямо­кутних трикутників за формулами: a = 2n +1; в = 2n²+2n; c = 2n² + 2n +1, де a і b  катети, c  гіпотенуза.

Залучаючи учнів у пошук математич­них закономірностей, навчаємо їх розмірковувати, робити висновки з фактів, тобто виховуємо пізнавальну активність  важливу умову розвитку творчих здібностей. Ці математичні уроки-дослідництва, на нашу думку, доцільно проводити, дотриму­ючись процесу наукової творчості: спостереження фактів висунення, формування і доведення гіпотези, аналіз отриманих результатів, вияв­лення наслідків.

Велике значення для розвитку інтелекту та мислення учнів мають творчі за­дачі з кількома різними способами розв’язання. Д. Пойа стверджував, що краще розв’язати одну задачу кількома спо­собами, ніж кілька різних чи однотипних задач [19, с.45]. Ми також дотримуємося такої думки, тим паче, що розв’язування  задач  різними способами залучає учнів до пошукової діяльності, створюючи умови для розвитку їх критичного мислення. Цього принципу дотримуємося при порівнянні різних розв’язків завдань, оцінюванні їх нестандарт­ності, складності в обчисленнях, доступності, новизни.

Розглянемо задачі на спільну роботу, які зустрічаються в курсі математики 6 класу. У розв’язанні цих задач велику роль відіграють такі величини: частина всієї роботи, яку виконує робітник (бригада, машина) за одиницю часу; час, який було витрачено на роботу; частина роботи, яку було виконано.

Задача №1. Одна бригада може виконати певну роботу за 10 днів, друга  за 15 днів. За скільки днів обидві бригади, працюючи разом, виконають цю роботу?

Розв’язання. 1-й спосіб.  Перша бригада виконує роботу за 10 днів, тобто за 1 день вона виконує   роботи. Друга бригада виконує за 1 день роботи. Це означає, що, працюючи разом, обидві бригади виконають +   частину усієї роботи.

1   6 (днів)  за такий час буде виконана вся робота. Відповідь: вся робота буде виконана за 6 днів. Зверніть увагу: оскільки ми розглядаємо частини роботи, немає сенсу говорити, що всю роботу приймаємо за 1. Цю ж задачу ми можемо розв’язати за допомогою рівняння. Для розв’язування задач цим способом зручно користуватися таблицями. Але це  є  не обов’язковим.

2-й спосіб. Перша бригада виконує роботу за 10 днів, тобто за 1 день вона виконує  роботи. Друга бригада виконує за 1 день роботи. Це означає, що, працюючи разом, обидві бригади виконають всю роботу за х днів:

  + 

=

Звідси маємо: 5x  30, х  6 днів необхідно двом бригадам, щоб впоратись з роботою.

Відповідь: 6 днів.

Розв'язування однієї задачі кількома способами активізує навчальну діяльність школярів, прививає інтерес до предмету. До розв’язування задач декількома способами учнів слід привчати поступово. Можна на уроці розглянути один або два способи, а пошук інших способів пропонується на домашнє завдання. Можливо, запропоновані учнями способи розв’язування не завжди  раціональні, проте для навчальних і виховних цілей така робота дуже важлива: учні  з  великою  зацікавленістю знаходяться  у пошуках, перебираючи у пам’яті варіанти використання вивчених теорем, відомих прийомів і методів розв’язування задач. Розглянемо це на прикладі твердження «Діагоналі ромба перетинаються під прямим кутом», з яким учні вперше зустрічаються при вивченні теми «Ромб та його властивості»:

І спосіб доведення.

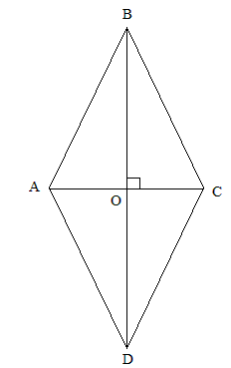Нехай діагоналі ромба ABCD перетинаються в точці О. Оскільки сторони ромба  рівні, то трикутник ABC рівнобедрений з основою АС. BO  медіана, бісектриса і висота ABC. Отже, діагоналі ромба перетинаються під прямим кутом.

Разом з тим, на уроці можна розглянути й інший спосіб доведення вказаної властивості ромба. Нехай ∠BAD = , ∠ABC= 180° — (сума будь-яких двох сусідніх кутів ромба рівна 180°). Діагоналі ромба є бісектрисами його кутів, бо ABO = BOC = DOC = AOD (за ІІІ ознакою рівності: AB=BC=CD=AD, як сторони ромба, AO = OC, BO = OD, діагоналі точкою перетину діляться навпіл).

Тобто ∠ BAО= ∠OAD = ; ∠АBO=∠BOC = = 90 -

Розглянемо ABО: Нехай ∠AOB = , тоді: + 90 - + = 180, (як сума внутрішніх кутів трикутника), = 90  отже, BD⊥AC, що і треба було довести.

Майже кожна задача з шкільного курсу математики допускає два чи кілька способів розв'язування.  Процес навчання розв’язувати геометричні задачі різними способами дає вчителю можливість спонукати учнів до більш вдумливого вивчення геометрії, а учням більш повно дослідити властивості геометричних  фігур  чи  одержати  цікаве  узагальнення  задачі і т.д.

Керівна  роль вчителя під час пошуку інших варіантів розв’язування дуже важлива. Він сам повинен добре  розв’язувати задачі, знати наперед, скількома способами можна знайти відповідь у кожній з них, ефективно використовувати при цьому час уроку. Як правило, пошуки різних способів розв’язування дуже зацікавлюють учнів, особливо здібних до математики. Поки вчитель розв’язує задачу одним способом з рештою класу, здібні до математики діти вже встигають знайти кілька інших способів. Розв’язування задач різними способами веде до розвитку вмінь всебічно аналізувати задану задачу.

Як на етапі вивчення нового матеріалу, так і на етапі його закріплення пропонуємо учням творчі завдання на складання задач. Іноді задача розв’язується просто, але підхід до її розв’язання нестандартний. Вивчаючи тему «Подільність  чисел» у  6 класі, звертаємо увагу на задачі такого типу:

Задача. Учень купив  три однакові  зошити і блокнот за 12 гривень. За всю покупку дав продавцеві 20 гривень і отримав здачі одну гривню. Чи правильно зроблено розрахунок продавцем, якщо вартість зошита виражається цілим числом гривень?

Задача. Марійка купила декілька кілограмів  лимонів  по  12 гривень за  кілограм і 3 кілограми апельсинів. Вказати можливу суму грошей за покупку, якщо  кілограм  апельсинів  коштує  ціле  число  гривень.

До речі, задачі такого змісту часто зустрічаються серед завдань ЗНО.

Проаналізувавши підручники з алгебри для учнів сьомого класу, бачимо, що майже всі автори для виведення даних формул використовують лише аналітичний метод. Розвитку дивергентного мислення, просторової уяви учнів сприяє  використання геометричного методу доведення даних формул.

Розглянемо  детальніше  матеріал  для  формули  різниці  кубів.

З метою актуалізації опорних знань, необхідно нагадати учням геометричний  зміст  поняття  «куб  числа».

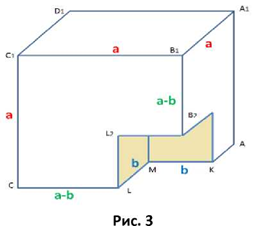
Нехай маємо два куба зі сторонами а та b (рис. 1).

Тоді їх об'єми відповідно  дорівнюють V₁ = а³  та  V₂ = b³.

 

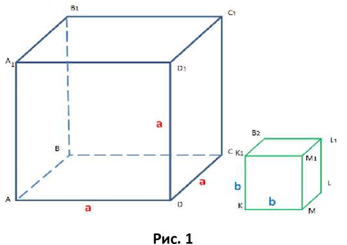
В  середині куба зі стороною а побудуємо куб зі стороною b, так щоб хоча б одна з  його  вершин збігалася з вершиною іншого, а три вершини лежали на ребрах  великого  куба (рис. 2).

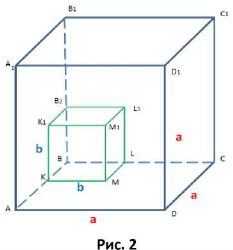
Оскільки розглядається формула різниці кубів, то «виріжемо» з куба зі стороною  а  куб  зі  стороною  b (рис. 3).

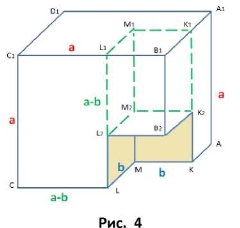
Для розвитку просторової уяви учнів на цьому етапі важливо дати їм можливість спочатку уявити, а уже потім «розглянути дану фігуру з усіх сторін». Під  керівництвом учителя без опори на рисунок учні мають самостійно  визначити  наступний  крок  виведення  даної  формули (рис. 4).

 

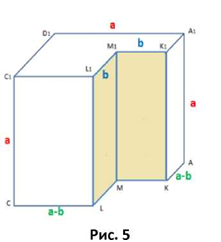
Відріжемо  паралелепіпед зі сторонами (а  b), b, b. Його об'єм дорівнює V₃ = (а  b)b².  Отримаємо  фігуру  на  рисунку 5.

Для кращого розуміння матеріалу, доцільно звертати увагу учнів на окремі  елементи проектованої  фігури (рис. 6).

 

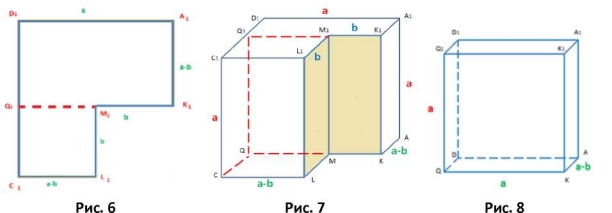
Наступним кроком «відтинаємо» паралелепіпед зі сторонами (а - b), а, b. Об'єм  даної  фігури  рівний V₄ = (а  b)аb (рис. 7).

Залишився паралелепіпед зі сторонами (а - b), а, а. Його об'єм дорівнює V₅ = (а  b)а² (рис.8).

Об'єм куба зі стороною a дорівнює сумі об'ємів вище згаданих фігур, тобто

V₁ = V₂ + V₃ + V₄ + V₅.

V₁  V₂ = V₃+V₄ + V₅.

Маємо, що а³  b³ = (а  b)b² + (а  b)ab + (а  b)a².

Винесемо  спільний  множник  за  дужки:

а³  b³ = (а  b)(b² + ab + а³).

За допомогою використання знань геометричного матеріалу вдалося вивести  формули  скороченого  множення.

Отже, доведення теорем та розв'язування задач різними способами привчає учнів: творчо мислити; самостійно висувати та перевіряти гіпотези; раціонально  планувати пошук розв'язування задачі; порівнювати та аналізувати  отримані результати; пізнавати основні методи розв'язування задач, складові  евристичних  алгоритмів  тощо.

 

2.2. Методичні рекомендації щодо системи розв’язування творчих завдань у процесі вивчення математики

 

У стандартних освітянських програмах дуже мало приділялось уваги творчим процесам. Творчість завжди відсувалась на другий план в освіті. І на сьогоднішній день  досить часто вчителі переслідують мету дати учням якомога більше знань з математики, сприяти розв’язуванню якомога більшої кількості типових задач, не враховуючи те, що, по-перше, великий потік навчальної інформації вступає в протиріччя з раціональним методом мисленнєвої діяльності учня і приводить до розумової безпорадності, хаотичної поспішності при зустрічі з труднощами; по-друге, сприяє формуванню стереотипності в процесі застосування знань. 

Ми привчаємо дітей до стереотипного мислення, сковуємо їх ініціативу, а потім вони вже самі для себе придумують у кожному конкретному випадку обмеження, які багатьом з них не дають, можливості побачити нешаблонні варіанти або способи під час аналізу і розв'язування завдань.

Побачити ж незвичайний хід розв'язування задачі може тільки людина смілива у  діях, яка вміє зосередити свою увагу на об'єктах задачі. Тому, бажано, щоб на кожному уроці, крім завдання вивчити деякий програмовий матеріал, повинна стояти «надзадача»: на базі досліджуваного матеріалу розвивати творчість, формувати в учнів прийоми, які б вони могли використовувати під час самостійної діяльності.

Тому завдання вчителя  організувати процес навчання так, щоб кожне зусилля з оволодіння знаннями проходило в умовах розвитку пізнавальних здібностей учнів, творчого мислення, формування в них таких основних прийомів  розумової  діяльності, як  аналіз, синтез, абстрагування, узагальнення, порівняння тощо. Учнів необхідно вчити самостійно працювати, висловлювати  і  перевіряти гіпотези, вміти робити узагальнення  досліджуваних  фактів, творчо  застосовувати  знання  в нових  ситуаціях.

Методисти  звертають увагу вчителів на важливість розв’язування учнями задач  декількома  способами. Проте, за  спостере­женнями, можна зазначити, що на уроках, як правило, розгляда­ється лише один зі способів розв’язання задачі, причому не  завжди раціональний. У таких випадках учитель наводить аргументи  про відсутність достатньої кількості часу на розв’язання однієї задачі  різними  способами. Така  аргументація  не  має під собою  підґрунтя: для  математичного  розвитку  учнів  набагато корисніше одну задачу розв’язати  кількома способами (якщо це можливо) і не шкодувати на це часу, ніж кілька однотипних задач одним способом. Із різних способів розв’язання однієї і тієї задачі треба запропонувати учням вибрати найраціональніший.

Під  час пошуку різних способів розв’язання задач в учнів  формується  пізнавальний інтерес, розвиваються творчі здібності, виробляються дослідницькі  навички. Після знаходження черго­вого методу розв’язання задачі учень, як правило, отримує велике моральне задоволення. Тому  вчителеві  важливо заохочувати пошук різних способів розв’язання задач, а не  прагнути нав’язувати своє розв’язання. Загальні  методи  розв’язання  задач повинні стати міц­ним надбанням учнів, але поряд із цим потрібно формувати в них уміння використовувати індивідуальні особливості кожної задачі, які дозволяють розв’язати її простіше. Саме  відхід  від шаблону, конкретний   аналіз  умов  задачі   є  запорукою  її  успішного  розв’язання.

Особливу увагу слід звертати на розв’язання задач арифметич­ним способом, тому що  саме  застосування  такого способу  сприяє розвитку в учнів  оригінальності  мислення,  винахідливості.

Спостереження показують, що учні, ознайомившись зі способом розв’язання задач за допомогою рівняння, не обтяжують себе глибо­ким аналізом умови задачі, намагаються якомога швидше скласти рівняння і перейти до його розв’язання. При цьому і введення позна­чень, і схема розв’язання, як правило, відповідає певним шаблонам.

У цьому випадку завдання вчителя  показати учням на при­кладах, що розв’язування задач за шаблоном часто призводить до значного збільшення обсягу  роботи, а  іноді  й  до ускладнення розв’язання, у результаті чого зростає можливість виникнення по­милок. Тому учням, перш ніж складати рівняння для розв’язання задачі, доцільно запропонувати уважно вивчити умову  задачі, по­думати  над тим, який спосіб розв’язання найбільш відповідає її умові, спробувати розв’язати задачу без використання рівнянь, арифметичним способом. Як  приклад  розглянемо  задачу.

Задача. Двоє  мотоциклістів виїхали одночасно  з  пунктів A і B назустріч один одному і зустрілися за 50 км від пункту B. При­бувши до пунктів A і B, мотоциклісти  відразу  повернули  назад і зустрілися знову  за  25  км  від пункту A. Чому  дорівнює  відстань між пунктами A і B?

Розв’язання цієї задачі за допомогою рівняння становить для учнів певні труднощі.  Набагато простіше розв’язати цю задачу, не складаючи рівнян­ня, а міркуючи так. Від початку руху до першої зустрічі обидва мо­тоциклісти проїхали разом відстань, що дорівнює AB, а до момен­ту другої зустрічі проїхали  разом  утричі  більшу  відстань.

Отже, кожен із них до другої  зустрічі  проїхав утричі більшу відстань, ніж до першої. Мотоцикліст, який виїхав із пункту B, до першої зустрічі проїхав 50 км. Отже, до другої зустрічі він проїхав 150 км (50  3 150). Тому відстань  між  пунктами  A і B дорівнює 125  км (15025125).

За такого підходу цю задачу можуть розв’язати учні не тільки 8, але і 5 класу.

Арифметичний спосіб розв’язання задач у випадку, коли ал­горитмічний метод не приводить до результату, є одним із найкра­щих засобів розвитку самостійного мислення, формування умінь творчо застосовувати знання. За допомогою  спеціально  дібраних  за­дач, здатних зацікавити учнів своєю уявною простотою і тим, що їх розв’язання не є очевидним, можна показати учням  красу, простоту і витонченість логічного міркування, яке  призводить  до результату.

Розв’язуючи з учнями ту чи іншу задачу, учитель повинен прагнути до досягнення двох цілей. Перша  допомогти учневі розв’язати саме цю задачу, навчити  його розв’язувати задачі, ана­логічні розглянутій; друга  так розвинути здібності учня, щоб він у майбутньому зміг самостійно розв’язати будь-яку  задачу  шкіль­ного  курсу. Ці дві  цілі, безумовно, пов’язані між собою, оскільки, упоравшись із конкретною достатньо складною для нього задачею, учень  удосконалює  вміння  розв’язувати  задачі  загалом.

Тому для  досягнення другої  цілі  під  час  розв’язування задач декількома способами слід звертати увагу учнів не тільки на найраціональніший спосіб розв’язання задачі, а й на ті способи, які широко застосовують під час розв’язування інших задач і в деяких випадках виявляються  єдиними. Пояснимо сказане прикладами.

Розглянемо  задачу.

Задача. Доведіть,  що при будь-яких значеннях x і y правильна нерівність:

1) (x  3y)² + 10 (x3y)  +26 ˃0;

2) 4xy+24x – 10 у −5 x²−у²−30< 0.

Такий порядок розташування нерівностей підказує метод до­ведення другої нерівності: помноживши  обидві  частини  нерівності на (–1) і виконавши  тотожні  перетворення,  матимемо

(y  2x)²  + 10 (y 2х) + (x 2)² + 26 ˃0.

Дістали нерівність, аналогічну першій. Аналогічний також і спосіб його доведення. Однак другу нерівність доцільно довести і більш природним шляхом, який  застосовують під час доведення будь-яких нерівно­стей подібного  типу.  Розглянувши  квадратний  (щодо x) тричлен

− 5х² + (4у + 24) х  у²  10у  30,

  знайдемо, що  його  дискримінант  при  будь-яких  y  від’ємний

(D=−(2у−2) ² −20).

Оскільки коефіцієнт при x² теж менший від нуля, то задана нерів­ність справедлива  при  будь-яких  значеннях  x і y.

Цей  метод  можна  застосувати  і  під  час  розв’язування  такої  задачі.

Задача. При  яких  значеннях  x і y  вираз

z=x²+2xy +2y²+ 2x+ 4y+3

набуває найменшого значення? Знайдіть це значення.

Справді, квадратний (щодо x) тричлен

x²+х (2y +2) + 2у²+ 4y+3

набуває найменшого значення при

х= = =  у  1

Це  найменше  значення  так  само  нескладно  обчислити:

у² + 2у + 2 = (у + 1)² + 1

Отже, заданий квадратний тричлен набуває найменшого зна­чення, яке дорівнює  1, при  y = −1  і  x=0 (x= − у  1 = 1  1=0).

Для розвитку творчого мислення учня на уроках математики у школі необхідно створювати умови для використання нестандартних підходів. Це сприятиме вихованню творчої особистості, здатної самостійно мислити, генерувати оригінальні ідеї, приймати сміливі, нестандартні рішення. Творче, нестандартне  завдання в  більшості  випадків сприймається як виклик інтелекту і  породжує  потребу  реалізувати себе  в подоланні  перешкоди. Воно є  поштовхом до  інтелектуального зростання особистості, формування творчого потенціалу, який може бути реалізовано учнем у майбутньому в професійній діяльності. Найбільших успіхів можна досягнути, вміло використовуючи весь арсенал засобів навчання разом із різними методами, створюючи атмосферу доброзичливості й взаємоповаги, впливаючи на емоційну сферу школярів, формуючи ситуацію успіху для кожного учня, сприяючи розвиткові творчої особистості.

 

ВИСНОВКИ

 

Одним із шляхів впровадження Державного стандарту базової і повної загальної  середньої освіти у роботу вчителя математики є впровадження інноваційних педагогічних технологій, зокрема, методики ТРВЗ (теорія розв’язання винахідницьких задач). Вона необхідна для формування логічного мислення і виховання творчої особистості,  підготовленої до розв'язування складних  питань  в  різних  сферах  діяльності.

Під  методами  розв'язування  винахідницьких задач розуміють прийоми й алгоритми, які розроблені в рамках ТРВЗ. Методи, які застосовують у  зазначеній  технології, розвивають такі пізнавальні та творчі здібності, як уміння робити висновки, оперувати інформацію, аналізувати ситуації, передбачати наслідки;  здатність  винаходити  нові  оригінальні  ідеї, знаходити кілька  правильних  відповідей  та ін.

Зазначено, що математика як навчальний предмет надає широкі можливості для здійснення процесу формування та розвитку оперативності мислення учнів. Використання системи розв’язування творчих завдань (особливо нестандартних завдань підвищеного рівня складності) дає можливість педагогу вчити школярів міркувати, творити, шукати, узагальнювати, порівнювати. У такому аспекті уроки математики можна розглядати як різновид наукової творчості.

Наголошено, що розв’язання творчої задачі  украй складний процес. Нестандартною (творчою) називають задачу, алгоритм розв’язку якої наперед невідомий.   Для розв’язування  нестандартної задачі учень не має готової схеми дій, або задачу неможливо розв’язати відомими способами, до результату також  неможливо  перейти на  основі  прямого  відтворення  знань і операцій.

Дати  учням базу знань, що дозволить розв’язати будь-яку задачу творчого характеру  неможливо, бо творчі завдання якоюсь мірою неповторювані, а універсального методу, що дозволяє розв’язати будь-яку задачу немає. Навіть суворе дотримання всіх вказівок і слідування порадам вчителя не зможе творчий  процес відшукання вирішень творчих завдань укласти в певні схеми.

Узагальнено, що процес розв’язування будь-якої творчого (нестандартного)  завдання складається у послідовному застосуванні двох основних  операцій:

1. зведення (шляхом перетворення або переформулювання) творчої задачі до рівносильної їй, але уже стандартної;
2. розбиття нестандартної задачі на декілька стандартних підзадач.

Підсумовано, що  використання системи розв’язування творчих завдань на уроках математики  якнайкраще розвиває в учнів творче мислення, інтерес до навчання,  предмету. Треба  лише вдало добирати математичні завдання, щоб вони викликали цікавість у школярів. Адже пробудити інтерес до математики, навчати школярів творчо мислити  це найголовніша мета, до якої прагне вчитель у зв’язку з завданням підвищення ефективності процесу навчання математики. Цьому сприяють: практичне ознайомлення школярів з нестандартним підходом до розв’язання творчих завдань; вправляння в пошуках оригінальних рішень; багатогранна творча діяльність школярів, яка спрямована  на  формування  навичок  пошукової  праці.

Для вирішення цих завдань використовуємо різноманітні творчі вправи, запитання, цікаві задачі, логічні вправи, задачі-головоломки, задачі-жарти, дидактичні ігри, загадки, ребуси, які в свою чергу передбачають: встановлення суперечності; встановлення причинно-наслідкових зв’язків; встановлення схожості та різниці між об’єктами, що порівнюються; зіставлення різних варіантів та дії вибору; виділення певних закономірностей в навчальній інформації; доведення правильності виконаних практичних або розумових дій; пошук і виправлення припущених помилок; висування гіпотез, пропозицій, здійснення певного прогнозу наступних подій.

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1. Аніконова М. Активізація  творчої діяльності учнів на уроках математики. Математика.  2009.  № 23. С.1-6.
2. Балдіна Л.М. Розвиток творчої компетентності учнів на уроках математики. Математика в  школах  України.  2006.  № 29.  С. 14-16.
3. Белешко Д. Т., Віднічук М. А., Крайчук О. В. Методика розв’язування нестандартних  математичних  задач. Частина 1. Х. : Вид. група «Основа», 2017.  127 с.
4. Вознесенська Л.М. Розвиток творчої особистості учнів засобами математичних  ігор. Математика  в школах України. 2008. № 14-15.  С. 34-37.
5. Давід Д.О. Розвиток творчих здібностей учнів на уроках математики. Математика. 2006.  № 45.  С. 1-6.
6. Державний стандарт базової і повної середньої освіти: Постанова Кабінету Міністрів України від 23.11.2011 р.  №1392 URL: http://zakon2.rada.gov.ua/laws/show/1392-2011-%D0%BF
7. Дичкiвська I.М. Основи педагогiчної iнноватики : навчальний посiбник. Рiвне : Зелент, 2001.  222 с.
8. Друзь Б.Г. Творчі вправи з математики для початкових класів: Посібник для вчителів.  К.: Рад. шк., 1998.  144 с.
9. Косоромова Ю. Використання творчих завдань на уроках математики. Психолог.  2004.  № 21-22.  С. 89-94.
10. Крамаренко А.В. Проблеми  творчого  розвитку учнів. Математика.  2004. №  27-28.  С.1-6
11. Крилова Л.П.Технологія ТРВЗ  шлях до творчого розвитку дітей на уроках математики. Збiрник наукових праць фiзико-математичного факультету СДПУ.  2012.  №2.  С.181-188
12. Крисинська І.В. Розвиток творчих здібностей дітей. Математика.  2004.  № 27-28.  С. 6-13.
13. Кушнір В. Особливості творчості у розв’язуванні задач. Математика в школі.  2010.  № 10.  С. 8-17.
14. Макаров С. Формування творчих здібностей учнів у процесі розв’язування  задач різними  засобами. Математика в школі.  2003.  № 9.  С. 28-31.
15. Макрiдiна Л.О. Технологiя творчостi ТРВЗ. Управлiння школою.  2003.  № 32  С. 12-26.
16. Макушенко Т.Г. Розвиток творчого мислення учнів на уроках математики. Математика в школах України.  2004.  № 6.  С. 17-23.
17. Малицька Л.В. Розвиток здібностей учнів на уроках математики. Математика  в  школах України.  2007. № 15.  С. 16-21.
18. Мойсеєнко Л.А. Психологія розуміння творчих  математичних задач на різних етапах їх розв’язування. Педагогіка і психологія. 2001. № 3-4. С. 117-124.
19. Пойа Д. Как решать задачу. Львов: Журнал «Квантор», 1991.  215 с.
20. Пушкіна З.П. Активізація розумової активності та розвиток творчої ініціативи на уроках математики. Математика в школах України. 2005. – № 5.  С. 2-6.
21. Сухомлинський В.О. Серце вiддаю дiтям. К.: Рад. шк., 1984.  288 с.
22. Швець В. Формування і розвиток здібностей учнів 5-6 класів під час навчання математики. Математика в школі.  2010.  № 5.  С. 19-24.

ДОДАТОК

РОЗВ’ЯЗУВАННЯ  ТВОРЧИХ ЗАВДАНЬ  З  МАТЕМАТИКИ

В  5-6 КЛАСАХ

 

Задача 1: На  запитання, скiльки  важить рибина, рибалка вiдповiв: «Хвiст важить 150 г, голова стiльки, скiльки хвiст i половина тулуба, а тулуб – скiльки  голова i хвiст разом». Скiльки  важить цiла рибина?

Розв’язання: Вага голови дорiвнює вазi хвоста плюс (+) половина ваги тулуба. Із умови задачi виходить, що вага тулуба дорівнює вазi хвоста плюс (+) половина ваги тулуба, плюс (+) вага хвоста. Значить половина ваги тулуба дорiвнює  вазi  двох хвостiв, тобто 150 х 2 = 300г, а весь тулуб важить 600г i тодi  вага голови дорiвнює: 150 + 300 + 450г. Тодi вага риби дорiвнює: 450 + 600 + 150 = 1200г = 1кг 200г.

Задача 2: В Аравії помирав старий чоловiк. Все своє майно, 17 верблюдiв, він заповiдав синам, причому старший мав одержати половину, середнiй  третину а найменший  дев’яту частину. Пiсля  смертi батька сини не знали, що робити, бо 17 не дiлилося без остачi нi на 2, нi на 3, нi на 9. Довго сперечалися  брати, аж  тут пiд’їхав до них на  верблюдi мудрець. Довiдався про суперечку i дав братам мудру пораду, яка  й допомогла роздiлити майно так, як заповiв батько. Що то була за порада?

Розв’язання: Мудрець вiддав братам свого верблюда, верблюдiв стало 18. Тодi їх подiлили вiдповiдно до батькового заповiту. Старший одержав 9, середнiй  6, молодший  2. Усього  17. А мудрець забрав свого верблюда й поїхав  далi.

Задача 3: По вулицi йшла дiвчинка. Зустрiвши дiдуся, вона привiталась. Дiдусь сказав: «Добрий день, маленька дiвчинко!» Дiвчинка заперечила, що вона не мала, i коли дiдусь запитав скiльки їй рокiв, то вона вiдповiла: «в 2 рази молодша мами, а  мама на 5 рокiв молодша батька. Разом нам 60 рокiв.» Скiльки рокiв дiвчинцi?

Розв’язання: Роки дiвчинки приймемо за 1 частину, тодi роки мами складуть двi частини, а батька  двi частини + 5 рокiв. І так, п’ять частин складають  55 рокiв,  а  на  одну  частину  припадає  55 : 5 = 11 рокiв.

Задача 4:  В недiлю рибалка ловив  рибу 3 рази: вранцi, вдень i ввечерi. Весь улов  3кг, причому, вранцi вiн зловив в 3 рази бiльше, нiж увечерi, а вдень стiльки ж, скiлъки і ввечерi. Скiльки риби зловив рибалка вранцi i ввечерi?

Розв’язання: Вилов риби ввечерi  одна частина, вранцi  три частини, а вдень  одна частина. Отже, весь улов складає 1 + 3 + 1 = 5 частин; 3кг = 5 частин, тодi  на  одну  частину  припадає 3000 : 5 = 600г (це вечiрнiй улов), 600 х 1800 г (ранiшнiй улов).

Задача 5:  Сашко витрачає на дорогу в школу 12 хвилин, а Марiйка 18 хв. Через 3 хвилини пiсля виходу Марiйки до школи вийшов Сашко. Через який час вiн її наздожене?

Розв’язання: На  пiвшляху. Оскiльки Марiйка витрачає на дорогу в школу в пiвтора рази бiльше часу, нiж Сашко, то через 6 хвилин Сашко її наздожене, пройшовши половину шляху, а  Марiйка  за  той  самий час також пройде  половину  всього  шляху.

Задача 6: Ставок заростає лататтям. Площа, яку покриває латаття, з кожним днем подвоюється. На десятий день заросла половина ставку. Яка частина  ставку заросла  на  дев’ятий  день?

Розв’язання: Оскільки площа, яку покриває латаття збільшується щоденно вдвічі  і  на  десятий день заросла половини ставка, то на дев’ятий день заросла половина половини ставка, тобто четверта його частина.

Задача 7: На уроках домоведення дiвчатка навчились пiдсмажувати шматочки хлiба. Пiдсмаживши одну сторону шматочка, на що йде 2 хв., його перевертають на  другу  сторону i смажать ще 2 хв. Сестра вирiшила пригостити нас 3 шматочками, але на сковорiдку можна положити тiльки 2 шматочки. Але вона не розгубилась і пiдсмажила 3 шматочки за 6 хв. Яким чином  вона  це  зробила?

Розв’язання: Через 2 хв. дiвчинка перевернула один шматочок, а на мiсце другого поклала третiй шматочок. Через 4 хвилини перший шматочок зняла, третiй  перевернула i поклала на другу сторону другий шматочок.

Задача 8: Маємо три купи каменів: у першій  10, у другій 15, у третій – 20. За  хід  дозволяється  розділити  будь-яку купу на дві менші; програє той, хто не може зробити хід. Який гравець виграє в цій грі?

Розв’язання: Наприкінці  гри  коли не можна зробити хід, маємо 45 куп по  одному  каменю. За  будь-який хід куп збільшується на одиницю, тому  вся гра має тривати точно 45-3=42 ходи. Отже,  другий  гравець  завжди  виграє.

Задачі за мотивами українських казок

 

 Кривенька  качечка

«Кривенька качеч­ка»  українська народна казка. Розповідає про бездітних діда й бабу, які вря­тували качечку. Згодом качка відвідує діда у вигля­ді дівчини й намагається віддячити дарунком. Дід і баба, всупереч обіцянці, підглядають за робо­тою дівчини й бачать, що вона  це врятована ними качечка. Через пору­шення угоди дівчина наза­вжди перетворюється на качечку й  покидає  діда  й  бабу.

Задача 1

Перший табунок качок, пролітаючи над ді­довою хатою, скинув Кривенькій Качечці за 6 хв 54 г пір’я, а другий табун  за 5 хв скинув 50 г пір’я. За  який  час  качки, скидаючи  пір’я  ра­зом, подарують Кривенькій  Качечці 152 г пір’я?

Задача 2

Поки Дід із Бабою ходили за грибами, Кри­венька Качечка пекла їм хліб. Із 5 кг борошна у неї виходило 7 кг хліба. Скільки треба бо­рошна, щоб випекти 35  кг хліба?

Задача 3.

Дід з Бабою збирали в лісі гриби. Дід за 7 год зібрав 112 грибів, а Баба за 5 год  105  грибів. Хто з них збирає за годину більше грибів і на скільки?

 Дев’ять  братів і  десята  сестриця Галя

 «Дев’ять  братів  і  десята сестриця Галя» — со­ціальне оповідання-казка  Марка  Вовчка.

 Зображує життя української бідноти (на прикладі вдови з десятьма дітьми) у часи панської екс­плуатації (кріпацтва). Головна ідея оповідання: засудження панської жорстокості, підступності, прагнення до збагачення на праці знедоленого люду, возвеличення краси українського народу, щирості, доброти,  поваги  одне  до  одного.

 Задача 4

Матері братів і сестриці Галі 36 років. Як­що вік її першого сина помножити на 3 і добу­ток збільшити на 3 роки, то дістанемо вік його матері. Скільки років першому синові вдови?

Задача 5

Щоб зварити дітям куліш, мати спочатку взяла половину всього пшона, що було в тор­бинці, а потім  ще 200 г. Після  цього  в  тор­бині  залишилось 400  г  пшона. Скільки  пшона  було  в  торбині  спочатку?

 Рукавичка

«Рукавичка»  українська народна казка. Роз­повідає про пригоду, яку пережили герої казки: Мишка-шкряботушка, Жабка-стрекотушка, Зайчик- побігайчик, Лисичка-сестричка, Кабан-іклан, Ведмідь- набрідь, коли вони оселилися  в  рукавичці.  Ця  казка про доброту, толерантність, повагу один до одного, готовність  допомагати  один  одному.

Задача 6

Якщо до числа звірів, що живуть у рука­вичці, додати ще таку саму кількість  звірів, то  дістанемо  14  звірів. Скільки  звірів  у  рукавичці?

Задача 7

Відстань від Дідової Собачки до рукавички дорівнює 12 км. Собачка пробігла  її  в  одному напрямі зі швидкістю 8 км/год, а в зворотно­му  на 2 км повільніше, оскільки  несла ру­кавичку. Скільки часу бігала собачка?

Пан  Коцький

«Пан Коцький» — українська  народна казка. Весе­ла історія про хитрість кота, який зумів налякати лісних звірів, про непрості стосунки диких і домашніх тварин. Цю казку можна вважати першим підруч­ником із культури, адже в смішних образах і діалогах персонажів висміюються людські вади.

Задача 8

Звірі збирались зварити обід для Пана Коцького. Вовк приніс 2 кг 700 г м’яса, Дикий Кабан приніс картоплі, маса якої на 1 кг 600 г більша ніж маса м’яса, а заєць приніс капусти, маса якої на 800 г менша від маси м’яса. На скільки маса м’яса більша ніж маса овочів?

Ведмідь і лисиця

«Ведмідь і лиси­ця» — українська народ­на казка. Хитрій Лисиці схотілося меду, вона обманула Ведмедя, за­лізла до нього на горище і з’їла весь мед. Проте її обман викрився, щойно вони з едмедем почали пекти млинці.

Задача 9

Першого дня Ли­сиця з’їла 0,4 меду, який Ведмідь заготу­вав на зиму, другого дня  на 5 % менше ніж першого, а третього  решту 900 г. Скільки меду  заготував  Ведмідь?

Задача 10

Під час випікання млинців для пригощан­ня Лисиці у Ведмедя з 1 кг борошна виходило 1,8 кг млинців. Скільки потрібно борошна, щоб напекти 5 кг млинців?

Солом’яний  бичок

«Солом’яний Би­чок» — українська на­родна казка  про одві­чну  мрію людей про краще життя. За сю­жетом казки Дід на прохання Баби зробив їй Солом’яного Бичка із засмоленим боком. Зві­рів, що зав’язли зубами в боці Солом’яного  Бич­ка, дід посадив у льох, а потім їх випустив. Звірі за це принесли  Діду  подарунки.

Задача 11

Ведмідь приніс Діду 5 кг меду, що станови­ло 40 % всього меду у вулику. Скільки всього меду у вулику Ведмедя?

Задача 12

Вовк першого дня пригнав Дідові 25 овець, а другого дня  23 вівці. На скільки  відсотків  менше  пригнав  Вовк  овець другого дня, ніж першого?

Задача 13

Вовк першого дня пригнав Дідові 25 овець, а другого дня  на 8 % менше, ніж першого. Дід продав усіх овець, що пригнав Вовк, і купив 4 воли. Скільки овець віддав  Дід за 1 вола?

Задача 14

Лисичка принесла Дідові з Бабою курей і гусей. За 18 днів 10 птахів споживають 90 кг зерна. Скільки потрібно зерна для 15 птахів на 24 дні?

Фарбований  лис

«Фарбований Лис» — цікава та повчальна казка Івана Франка. Через необережність Лис потрапив у діжку із синьою фарбою і пере­творився на страшне чудовисько. Проте він був хитрим і кмітли­вим, використав обман для свого звеличення. А брехня завжди колись викривається, тому Лис і постраждав.

Задача 15

У діжці, що стала у пригоді для схованки Лису Микиті, була синя фарба і олія у відно­шенні 3:2. Скільки синьої фарби і скільки олії було у діжці, якщо всього було 91,5 кг розчину?

Задача 16

Усе тіло Лиса було затоплене у фарбі, із діжки стирчала тільки голова. Довжина голови Лиса Микити дорівнює 20 см, що становить 15 частину його зросту (разом із хвостом). Який зріст у Лиса?