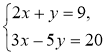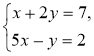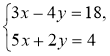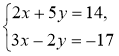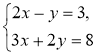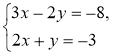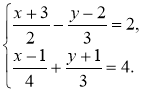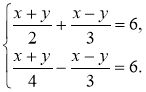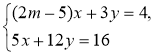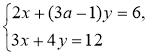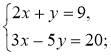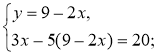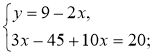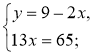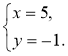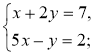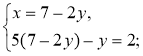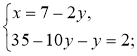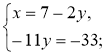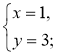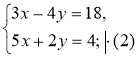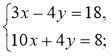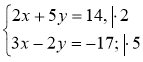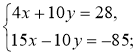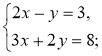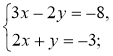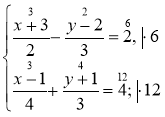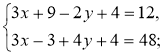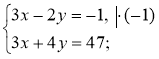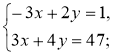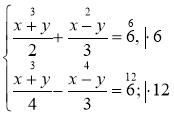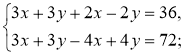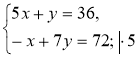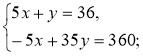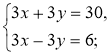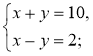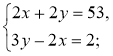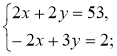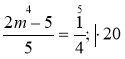Системи лінійних рівнянь із двома змінними
Тема. Системи лінійних рівнянь із двома змінними
Мета: перевірити рівень опанування учнями навчального матеріалу та вироблених умінь і навичок з теми, передбачених програмою з математики.
Тип уроку: контроль засвоєння знань, умінь, навичок.
Хід уроку
І. Організаційний момент
- Перевірка готовності до уроку.
- Зібрати зошити з домашньою контрольною роботою.
II. Умова тематичної контрольної роботи
|
Варіант 1 |
Варіант 2 |
|
1º. Розв'яжіть систему |
1º. Розв'яжіть систему |
|
2°. Розв'яжіть систему |
2°. Розв'яжіть систему |
|
3°. Розв'яжіть систему |
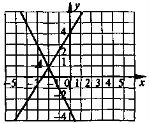
3°. Розв'яжіть систему |
|
4*. Розв'яжіть систему рівнянь
|
4*. Розв'яжіть систему рівнянь
|
|
5*. Розв'яжіть задачу, склавши систему із двома змінними. Із двох селищ одночасно назустріч одне одному вийшли два пішоходи й зустрілися через 3 години. Відстань між селищами 30 км. Один з пішоходів подолав до зустрічі на 6 км більше за іншого. Знайдіть швидкість кожного пішохода. |
5*. Розв'яжіть задачу, склавши систему рівнянь. Із двох міст, відстань між якими 53 км, одночасно виїхали назустріч один одному два велосипедисти й зустрілись через 2 години. Знайдіть швидкість кожного велосипедиста, якщо відомо, що другий велосипедист долає за 3 год на 18 км більше, ніж перший за 2 год. |
|
6**. При якому значенні параметра т система рівнянь |
6**. При якому значенні а система рівнянь |
III. Розв'язання та відповіді
|
Варіант 1 |
Варіант 2 |
|
1º. |
1°. Відповідь. (1; 3). |
|
2°. 13х = 26; х = 2; 3 · 2 – 4у = 18; 4у = -12; у =-3. Відповідь. (2; -3). |
2°. 19у = -57; у = -3; 2х – 15 = 14; 2х = 29; х = 14,5. Відповідь. (14,5; -3). |
|
3°.
у = 2х – 3
А(2; 1) Відповідь. (2; 1) |
3°.
у = -2х – 3
А(-2; 1) Відповідь. (-2; 1). |
|
4*.
6у = 48; у = 8; 3х – 16 = -1; 3х = 15; х = 5. Відповідь. (5; 8). |
4*.
36у = 396; у =11; 5х + 11 = 36; х = 5. Відповідь. (5; 11). |
|
5*. Нехай х (км/год) — швидкість першого пішохода, а у (км/год) — швидкість другого пішохода. Тоді за 3 год перший пішохід пройде 3х (км), а другий — 3у (км). А разом за 3 год вони подолають 30 км, тобто 3х + 3у = 30, причому перший пішохід подолав на 6 км більше за другого, отже, 3х – 3у = 6. Складемо й розв'яжемо систему рівнянь:
2х = 12; х = 6; у =10 – 6 = 4. Отже, швидкість першого пішохода 6 км/год, а другого — 4 км/год. Відповідь. 6 км/год, 4 км/год. |
5*. Нехай швидкість першого велосипедиста х (км/год), а другого у (км/год), тоді за 2 год до зустрічі перший подолав 2х (км), а другий — 2у (км), а разом 53 км. Отже, 2х + 2у = 53. Оскільки другий за 3 год долає 3у (км), а перший за 2 год — 2х (км), причому другий подолає на 18 км більше, то маємо: 3у – 2х = 2. Складемо й розв'яжемо систему рівнянь:
5у = 55; у =11; 2х + 22 = 53; 2х = 31; х = 15,5. Отже, швидкість першого велосипедиста 15,5 км/год, а другого — 11 км/год. Відповідь. 15,5 км/год, 11 км/год. |
|
6**. Система лінійних рівнянь має безліч розв'язків, якщо однойменні коефіцієнти пропорційні:
8m – 20 = 5; 8т = 25; т =
Відповідь. |
6**. Система лінійних рівнянь не має розв'язків, якщо коефіцієнти при х та у пропорційні, але їх відношення не дорівнюють відношенню вільних членів, тобто
9а – 3 = 8; a =
6a – 2 ≠ 4; 6а ≠ 8; а ≠
Відповідь. a = |
IV. Підсумки уроку
Учні отримують розв'язання завдань тематичного оцінювання № 8 для виконання самостійного аналізу помилок удома.
V. Домашнє завдання
Аналіз тематичної контрольної роботи (за готовим розв'язанням виконати завдання, в яких допущено помилки; визначити, які питання треба повторити.

про публікацію авторської розробки
Додати розробку