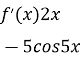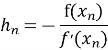Стаття "Метод послідовних наближень та розв`язування трансендентних рівнянь"

 

 

 

 

 

Метод послідовних наближень і розв'язування трансцендентних рівнянь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зміст

Вступ……………………………………………………………………………………3

Розділ 1.Метод послідовних наближень…………………………………………….5

1.    Принцип стискуючих відображень…………………………………5
2.    Метод простої ітерації……………………………………………….6

Розділ 2. Деякі методи розв’язування трансцендентних рівнянь………………….9

2.1 Метод січних………………………………………………………….9

2.2 Метод дотичних……………………………………………………...10

2.3 Метод хорд…………………………………………………………...14

2.4 Удосконалений метод хорд………………………………….............18

 Розділ 3. Приклади розв’язування трансцендентних рівнянь…………………….20

Висновки……………………………………………………………………………….24

Список використаних джерел………………………………………………………..26

 

ВСТУП

При вивченні математики в школі  дуже багато часу приділяють  розв’язуванню рівнянь і систем рівнянь. Спочатку це рівняння першого степеня і системи таких рівнянь. Потім появляються квадратні,  біквадратні і ірраціональні рівняння, а пізніше учень знайомиться з показниковими,  логарифмічними і тригонометричними рівняннями.  Така увага до рівнянь не випадкова.. Яку би область  застосування не взяти , найчастіше для одержання кінцевого результату потрібно розв’язувати рівняння чи систему рівнянь .

Під час математичних олімпіад часто пропонуються рівняння,які треба розв’язати методом послідовних наближень. Тому мета роботи – ознайомити читача з різними способами розв’язування трансцендентних рівнянь, тобто нелінійних рівнянь (показникових, логарифмічних, тригонометричних ), які побудовані на ідеї послідовних наближень. У роботі зібрано і класифіковано основні теоретичні відомості з даної теми. Методи розв’язування рівнянь  проілюстровано прикладами.

Якщо би математики обмежувалися вивченням рівнянь, які допускають точний розв’язок, тобто розв’язок по якійсь формулі, то розмова інженера з математиками мала би приблизно такий вигляд :

Інженер: При розрахунку побудови я прийшов до такого рівняння . Мені його треба терміново розв’язати – через місяць я повинен закінчити проект побудови.

Математик: Був би я радий допомогти вам, але для рівняння такого виду нема формули.

Інженер: Не зможете ви вивести цю формулу?

Математик : І пробувати не буду. Давно вже доведено,  що для таких рівнянь формули не існує.

В математиці розроблений цілий ряд способів наближеного розв’язування рівнянь. Велика частина способів наближеного розв’язку рівнянь побудована  на ідеї послідовних наближень. Ця ідея використовується  не тільки при розв’язуванні рівнянь, але і для розв’язування ряду практичних задач.

При складанні будь – якого плану ,  розкладу і т.д. спочатку  беруть деяке грубе наближення, яке потім послідовно  покращують, одержуючи  в кінці кінців потрібний результат.

 Обробку  деталі  в цехах заводу також   можна  розглядати, як послідовне наближення  до потрібної форми.  Спочатку беруть грубе наближення  - злиток чи яку – небудь  іншу заготовку. Цю заготовку обробляють  на станку,  придаючи їй форму, яка близька  до деталі,  яку треба виготовити. Після цього  її передають  на станок, який працює з великою точністю. Після декількох етапів обробітки,  тобто декількох наближень, і появляється потрібна деталь .

Вперше послідовні наближення зустрічаються у грецького філософа Зенона Елійського, який жив  за 500 років до нашої ери. Цей філософ  пробував довести,  що в природі не існує руху.  Доводив відсутність руху Зенон таким чином. Якщо найшвидший з греків – Ахіллес – попробує  догнати черепаху, то він ніколи не зможе цього зробити . Насправді,  нехай відстань між Ахіллесом і черепахою 100 кроків  і нехай Ахіллес  пробігає за 1 секунду 10 кроків , а черепаха проповзе  1 крок. Через 100 секунд Ахіллес пробіжить 1000 кроків, які відділяють його від черепахи. Але за цей черепаха відповзла на 100 кроків . Ще через 10 секунд Ахіллес пробіжить ті 100 кроків , але черепаха проповзе ще на 10 кроків вперед.  Щоби подолати  ці 10 кроків, Ахіллес затратить ще 1 секунду, за яку черепаха проповзе вперед на 1 крок. І так, черепаха весь час буде впереді , і він ніколи не наздожене черепаху.  Значить руху не існує.  Зрозуміло, це міркування Зенона – парадокс, але     не більше того. Рух є невід’ємною  властивістю матерії.

Міркування Зенона можна розглядати, як своєрідний метод наближеного розв’язування рівнянь.

Розв’язування рівнянь методом послідовних наближень пригодилось  у зв’язку з появою швидкодіючих електронно – обчислювальних машин. 

 

 

 

 

РОЗДІЛ 1. МЕТОД ПОСЛІДОВНИХ НАБЛИЖЕНЬ

 

При використанні сучасної обчислювальної техніки дуже зручні ітераційні методи. Ці методи застосовуються для приблизного розв`язання алгебраїчних і трансцендентних рівнянь, систем рівнянь і інших задач обчислювальної математики. Розв’язування рівнянь і систем рівнянь за допомогою ітераційного методу одержується  як границя  послідовних наближень, які обчислюються в ході процесу ітерації. Ітераційні методи часто називають також методами послідовних наближень.

При розв’язуванні задачі методом  послідовних наближень з самого початку задають деякі  приблизні значення невідомих.  З цих  невідомих наближень отримують нові «покращені» приблизні значення. Нові приблизні значення  знову «покращують» і т.д. При конкретних умовах  побудована таким чином послідовність наближень збігається  до точного розвитку.

В основі багатьох ітераційних методів лежить так званий принцип   стискуючих відображень. Цей принцип широко застосовується як при доведенні теорем існування  і єдності,  розв’язування рівнянь і систем рівнянь різних типів, так і при послідовній збіжності ітераційних методів.

1.1Принцип стискуючих відображень.

 Нехай х і у – два метричних простори. Будемо говорити, що оператор  у = Фх відображає Х в У, якщо  кожному елементу х є Х поставлений в відповідність елемент у є У.

Якщо Х =У, то цей оператор задає відображення Ф простору Х в себе.

Всяка точка х , яка переводиться відображенням Ф в себе називається нерухомою точкою цього відображення.

Означення . Нехай R - метричний простір, а оператор у = Фх відображає Rв себе. Якщо при деякому α, 0 <α<1 відображення у = Фх задовольняє умову                ρ( Фх; Фх′) ≤ αρ( х; х′) для будь яких х, х′ є R, то таке відображення називається стискуючим.

Теорема ( принцип стискуючих відображень) : Якщо відображення у= Фх стискуюче х є R, у: R R,  R – повний метричний простір, то існує одна і тільки одна нерухома точка цього відображення, тобто рівність х = Фх має єдиний розв’язок. Розв’язок  цього рівняння може бути знайдений як границя послідовності =Ф, k =1,2…, де - довільний елемент з R.

Точки , які одержані з формули , k= 1, 2 .., є послідовними наближеннями розв’язку х* рівняння х = Фх. Із одержаної вище нерівності ρ()≤ ρ(;, де  k<l; переходимо до границі при l і фіксуючому k ,одержимо ρ(;х*) ≤ ρ(;.  (1)

Остання нерівність дає оцінку відстані між точним розв’язком х*і його наближенням ..

1.2 Метод простої ітерації

Використаємо принцип стискуючих відображень для розв’язання  скалярного рівняння f( х) =0  ( 2)

F(x) -  дійсна функція дійсного  аргументу. Для розв’язування алгебраїчних і трансцендентних рівнянь виду  ( 2) розроблено багато різних ітераційних методів. Найчастіше по функції  f(х) будують функцію  φ(х), таку, що шуканий корінь х =х* рівняння (2) є і коренем рівняння х = φ(х)  (3)  і потім будують послідовність {}  за допомогою відношення.

=ϕ( ) k=1,2,…., (4) розпочинаючи  з деякого наближення . Збіжність послідовності  забезпечується відповідним вибором функції ϕ і початкового наближення Вибираючи різними способами функцію ϕ ( яка залежить від f(x)), можна одержати різні ітераційні методи.

Формула ( 4) визначає чисельний метод розв’язання  рівняння х = φ(х), який називають  методом простої ітерації. В нашому випадку метод простої ітерації має просту геометричну ітерацію. На малюнку зображено поведінку послідовних наближень випадку, коли 0< ϕ’(х)≤q<1.

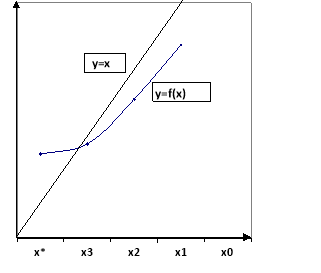
А на цьому малюнку – коли  -1< -q≤ (x) < 0  в деякому околі кореня. Із цього околу  і вибирається початкове наближення

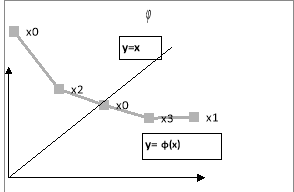
За допомогою цього методу допущена при обчисленні помилка ( яка не виходить за границі  відрізка R) не впливає на кінцевий результат ,  оскільки помилкове значення можна розглядати як нове початкове наближення. Властивість самовиправлення робить метод простої ітерації одним із надійніших методів обчислення.

Надалі будемо припускати, що рівняння (2)  має тільки ізольовані корені, тобто для кожного кореня рівняння  f(x) = 0, існує окіл, який не має інших коренів цього рівняння.

Приблизне знаходження ізольованих дійсних коренів рівняння (2) складається з двох етапів:

1.                   визначення коренів, тобто є встановлення  таких  проміжків, в кожному з яких існує один і тільки один корінь рівняння (2);
2.                   уточнення приблизних значень коренів ; тобто обчислення  кожного кореня тим чи іншим числовим методом з заданою точкою.

Для  визначення коренів корисна наступна теорема :

Якщо неперервна функція f(x) на кінцях відрізка  [a;b] приймає значення різних знаків, то всередині цього відрізка існує хоча б один корінь рівняння  f(x) = 0. Цей корінь буде єдиним,  якщо похідна (x) існує і зберігає постійний знак всередині інтервалу (a;b).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 2. ДЕЯКІ МЕТОДИ РОЗВЯЗУВАННЯ ТРАНСЦЕНДЕНТНИХ РІВНЯНЬ

 

2.1 Метод січних

Припустимо, що на деякому відрізку [a;b] функція f(x) неперервна  разом  з похідними (x)  і  (x), причому  f(x)f(b) <0 ,  а похідні не міняють свого знаку на інтервалі (a;b). Це означає, що на відрізку [a;b] існує єдиний корінь х=х* рівняння (2).

Якщо функція φ(х) неперервна в деякому околі х*, то рівняння (3) , де φ(х)=х-φ(х)f(x), (5) тоже має х* своїм коренем. Функцію φ(х) в (5) можна підібрати так, що ітераційний процес (4) для рівняння х = φ(х)= х-φ(х)f(x) буде збіжним.

Нехай - деяка точка  з відрізка [a;b] вибраного , як вказано вище, причому f()() >0  . В (5) в якості  функції φ(х) візьмемо функцію :

φ(х)=

Тоді  φ(х)=х-f(x)  і рівняння  х=   також має   корінь х*. Приймемо за початкове наближення будь – яку точку, достатньо близьку до х* точку   з відрізка [a;b] в якій f()  має знак, протилежний знаку - f(),  а наступні наближення будемо добувати звичайним способом:

    , k=1,2,…. (6)

Для оцінки точності наближення можна користуватися формулою              ׀-x*׀≤   (7)  , де . Дійсно f() = f() – f(x*) = (ξ) (x*) , де ξ знаходиться між і х*.

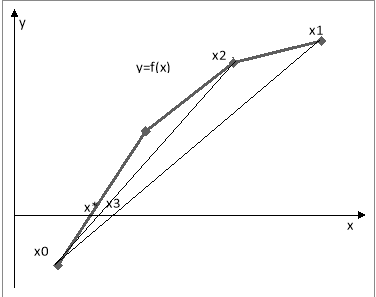
На малюнку дана геометрична інтерпретація ітераційного методу ( 6) : Значення є абсциса  точки січної прямої, яка проходить через точки (f()) і (; f()) з віссю х. У зв’язку з цією геометричною інтерпретацією метод ( 6)  називають метод січних

 

 

2.2 Метод дотичних

Ще одним класичним методом розв’язування  скалярного рівняння f(x) =0  є метод Ньютона. Покладемо в φ(х) = х – φ(х)f(x), φ(x)= .

 Тоді φ(х) =х-  і потрібно знайти  корінь х* рівняння  х = х- .

Як в попередньому випадку  припустимо, що на відрізку функція f(x) має неперервні , які не перетворюються в нуль похідні     і f(a)f(b)<0.  Маємо : , так що =0. В силу неперервності   знайдеться окіл точки х*, такий , що для всіх х є має місце нерівність : ׀≤ q<1.

Якщо початкове наближення взято із цього околу , то послідовність {}  побудована за формулами ,  k =0,1,…., буде збігатися до х*. Початкове наближення найкраще вибрати так, щоб була виконана умова f(>0.

Метод Ньютона має просту геометричну інтерпретацію : значення  є абсциса точки перетину дотичної до кривої y=f(x)  в точці  x<  з віссю х. Тому метод Ньютона часто називають методом дотичних

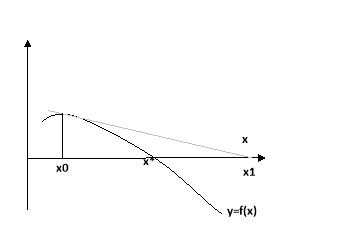
Якщо за початкове наближення в методі Ньютона взяти точку , таку , що f(<0, то як видно з малюнка ми можемо не прийти до кореня х=х*, якщо тільки початкове наближення не дуже добре.

Оцінимо швидкість збіжності методі Ньютона. За формулою Тейлора :

f(x*)= + (x* - )+(ξ) ( (ξ  знаходиться між х* і  . Так як  f(x*) =0, то = -x* - (.  Звідси , -x* = = (.

Якщо = a = = , то                                    ׀-x*׀≤ ׀ (8)

Нерівність (8)  гарантує  швидку збіжність методу Ньютона , якщо початкове  наближення таке, що ׀-x*׀≤с<1

Дійсно, в цьому випадку з нерівності ( 8) слідує :

׀-x*׀≤

Комбінуючи ці два методи , можна одержати метод знаходження дійсних коренів рівняння f(x)=0, такий , для якого послідовні наближення і будуть лежати по різні сторони від шуканого кореня. В послідовності наближення  до кореня ,  побудованому подібним методом,  наближення по недостачі і по надлишку чергуються, звідси:

׀-x*׀≤ ׀- ׀

Нехай, як і раніше , на кінцях відрізка функція f(x) приймає значення різних знаків, а і на цьому відрізку не міняють знаків . Задамо і формулами:

= .

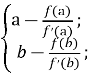
, а наступні наближення будемо шукати за формулами :

, (9)

=, n=1,2,… (10)

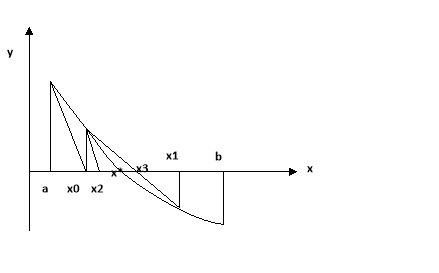
Не тяжко побачити, що послідовність наближень і завжди розміщені по різні сторони від х = х* і перші співпадаючі знаки значень і будуть правильними знаками для х = х*.

Приклад 1) Обчислити з точність 0,0001 додатній корінь рівняння:           

Спочатку відділимо корінь; для цього побудуємо графік и функції у = і    у =.

 

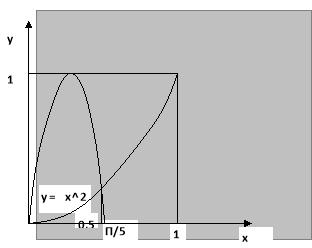
З графіка видно, що додатній корінь  рівняння знаходиться між 0,5 і

Попробуємо в якості початкового відрізка взяти відрізок [0,5; 0,6];на кінцях   цього відрізка функція f(x)= приймає значення різних знаків: f(0,5)<0 , f(0,6)>0  і дві похідні і на відрізку [0,5; 0,6] додатні ( не міняють знаку).

Для знаходження кореня скористаємося комбінованим методом. Припустимо , що а=0,5 ; b=0,6

Так як і >0, то  ; .

Далі послідовне наближення до кореня знаходимо за формулами ( 9 і 10); результати обчислень запишемо в таблицю.

Наближення	х			f(x)=
a	0,5	0,25	0,59847	-0,34847	-
b	0,6	0,36	0,14112	0,21888	6,14995
	0,56441	0,31856	0,31413	0,00443	5,87572
	0,56142	0,31519	0,32829	-0,01310	-
	0,56366	0,31771	0,31769	0,00002	-
	0,56360	0,31765	0,31797	-0,00032	-

 

Так як =0,00006<0,0001,  то потрібна степінь точності досягнута. Додатній  корінь х* рівняння знаходиться на інтервалі (0,56360;0,56366); можна покласти х*=0,5636 з абсолютною похибкою, меншою за 0,00006.

2.3  Метод хорд

Нехай нам потрібно розв’язати рівняння  f(x)=0. Це задача рівносильна задачі про знаходження точок , в яких графік функції y=f(x) перетинає вісь абсцис. Припустимо, що функція f(x) неперервна і має в точках а і b значення різних знаків. Тоді хоча б в одній точці відрізка [a;b]ця функція перетворюється в нуль. Іншими словам , хоча б в одній точці ξ  відрізка [a;b] графік функції y=f(x) перетинається з віссю абсцис. Загалом кажучи, таких точок може бути декілька.

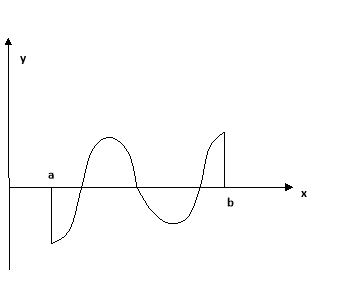
Але якщо функція y=f(x) монотонна на відрізку [a;b] і має на його кінцях значення різних знаків, то графік функції перетинається на цьому відрізку  з віссю абсцис лише в одній точці ξ. Щоб знайти наближено цю точку, замінимо на  відрізку [a;b] дугу кривої y=f(x) відповідною хордою MN і знайдемо точку перетину Т цієї хорди х віссю Ох.

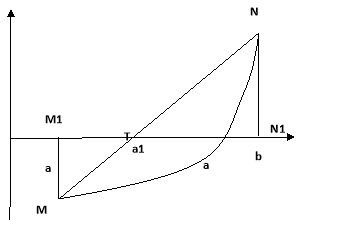
Для цього розглянемо подібні трикутники МТ і NT.З подібності  цих трикутників випливає, що . Але з малюнку видно, що Т= Т= b- , = -f(a)  і = f(b),де через позначена абсциса точки перетину хорди MN х віссю Ох. Тому : =

Розв’язуючи це рівняння , знайдемо, що .

Цю  рівність можна записати також у вигляді  (1)

Або =а - (2)

Число і є наближеним значенням кореня рівняння f(x)=0, яке лежить між точками а і b.

Так як знаки чисел і різні, то або знак , або знак відрізняються віз знака . Якщо в точках а і функція f(x) має різні знаки  то застосовують формулу (1) до відрізка [a;]  і виходить наступне наближення : =- f( (3) для шуканого  кореня. Якщо ж функція f(x) приймає значення різних знаків в точках а і b, то застосовують формулу (2) до відрізка [a;b] і вважають: =- f(  (4)

Знайшовши значення  , використовують формулу (1) до відрізку [(або відповідно формулу (2) до відрізку [;b] і знаходять наступні наближення . Взагалі, якщо вже знайдено наближення , то шукають наступні наближення за формулою:   (5)

Або за формулою (6)

Ми одержали дві формули. Подивимося, в якому випадку треба використовувати ту чи іншу формулу. Нехай крива  опукла вверх. В цьому випадку треба з’єднувати точки кривої з тим кінцем М чи , в якому функція додатна.  Якщо ж крива  опукла вниз, то треба з’єднувати точки кривої  з тим кінцем, в якому функція від’ємна. Різні виникаючі при цьому випадки зображені на  малюнку:

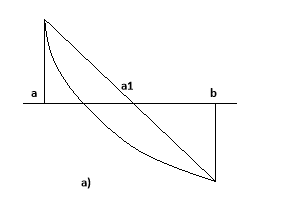
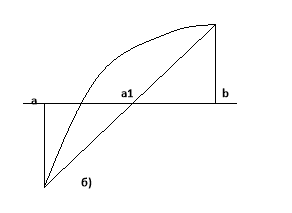
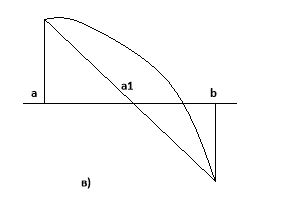
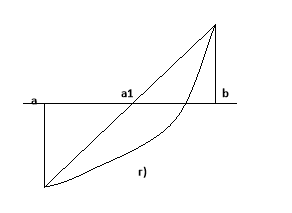
Ці малюнки дають геометрично очевидні наступні твердження:

Нехай на відрізку [a;b] функція f(x) неперервна, монотонна , має постійний напрям опуклості і приймає на кінцях відрізка значення різних знаків. Тоді при правильному виборі формули наближень метод хорд дає послідовність точок, яка збігається до кореня  рівняння f(x)=0. Якщо ж вибрати формулу неправильно, то метод хорд можна привести до того, що точка попаде за межі  відрізка [a;b]. Це зображено на малюнку.

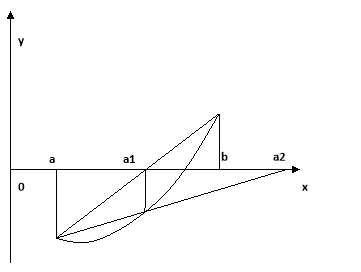
Описаний метод хорд є частинним випадком метода ітерації. Нехай функція f(x) не перетворюється в нуль при х=а. Тоді рівняння f(x)=0 рівносильне  рівнянню х=х- (7)

Дійсно, якщо )=, то =-- (8).

Для прикладу розв’яжемо методом хорд рівняння 2) +3х-1=0

Тут +3х-1. Так як то це рівняння має хоча б один корінь на відрізку [0;1]. Якщо намалювати графік функції у=+3х-1, то ми побачимо, що на відрізку [0;1] він  опуклий вверх. Тому використаємо формулу (1). За формулою (1) першим наближенням для цього кореня є число =1-3

Друге наближення знайдемо за формулою =. Дальше

Таким чином, з точністю до 0,001 корінь рівняння , який лежить на відрізку [0;1] дорівнює 0,322.

2.4 Удосконалений метод хорд

 Існує удосконалений метод хорд, який дає достатньо швидку збіжність. В звичайному методі хорд ми на кожному кроці використовуємо один  із кінців відрізка [a;b] і останнє одержане наближення. Замість цього можна використати два останніх наближення – адже вони звичайно ближче до шуканого кореня, чим кінці відрізка [a;b]. Формула , в якій  ми використовуємо два останніх наближення має вигляд (мал. а) :

(9)

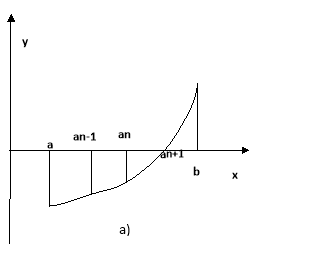
 При цьому обчислюється  за формулою (1), а - за формулою (3) або (4), в залежності від знаків f(a), f(b), f(:  якщо f(a)<0, f(b)>0, то при f(<0 вибирається формула (4), а при f(>0 – формула (3).

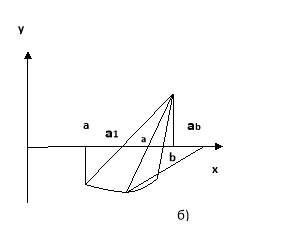
Якщо випадково виявиться, що точка , яка обчислена за формулою (9), лежить за межами відрізка [a;b], то на наступному кроці замість цієї точки треба взяти найближчий до неї кінець цього відрізка (мал. б)

Виявляється, що збіжність досконалішого методу хорд набагато швидша, чим звичайного. Саме тому , якщо ξ – корінь рівняння f(x)=0, то ׀,  (10)    де  t=

Для прикладу розв’яжемо цим методом те ж рівняння  3)+3х-1=0

Перше наближення і =0,31. Те ж , що і в звичайному методі хорд. Наступне наближення обчислюємо за формулою =0,3+0,040

Маємо  f(0,3223)=0,0004. Ясно, що х=0,3223 дає шуканий корінь з точністю до 0,0001.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

РОЗДІЛ 3. ПРИКЛАДИ РОЗВЯЗУВАННЯ ТРАНСЦЕНДЕНТНИХ РІВНЯНЬ

 

4)Знайти додатній корінь рівняння.

f(x)=

Розв’язування: Перш  за все відокремимо корінь. Так як f(1)=-0,6<0 i f(2)=5,6>0,  то шуканий корінь ξ лежить в інтервалі (1;2). Одержаний інтервал великий, тому розділимо його пополам. Так як  f(1,5)=1,425,  то 1<ξ<1,5.

 Послідовно використовуючи формулу =a+ , де

Будемо мати :  (1,5-1)=1+0,15=1,15;

f(=-0,173;

)=1,15+0,040=1,190;

Так як    маємо

0<ξ-<

Таким чином, ξ=1,198+0,0020,  де 0<Ѳ<1.

5)Обчислити за допомогою методу  Ньютона від’ємний корінь рівняння f(x)=  з п’ятьма правильними знаками.

Розв’язування . Покладемо в лівій частині рівняння х=0 ,-10,-100,…., одержимо f(0)=-10000, f(-10)=-1050, f(-100).

 Звідси, шуканий корінь ξ на інтервалі -100<ξ<-10. Звузимо даний інтервал . Так як f(-11)=3453, то  -11  <ξ<-10. В цьому останньому інтервалі і Так як f(-11)і  , то можемо взяти за початкове наближення Наступні наближення

n		f
0	-11	3453	-5183	0,7
1	-10,3	134,3	-4234	0,03
2	-10,27	37,8	-4196	0,009
3	-10,261	0,2	-	-

 

Зупиняючись на n=3, перевіримо знак значення f(

Так як f(-10,260)<0, то -10,261<ξ<-10,260,і будь – яке з цих двох чисел дає шукане наближення.

6)Знайти найменший додатній корінь рівняння tgx=x  з точністю до 0,0001 за методом Ньютона.

Розв’язування. Побудувавши графіки кривих у= tgx і у=х бачимо, що шуканий корінь ξ знаходиться в інтервалі π<ξ<

 

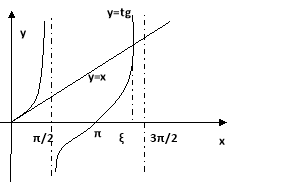
Переписавши рівняння у вигляді f(x)  будемо мати:

Звідси, <0 і <0, при  π<х<.

Так як f( то за початкове наближення можна взяти . Обчислення виконуємо по наступній схемі:

n		f
0		-1	-4,712	-0,212(
1	4,50004(257	-0,0291	-4,399	-0,0066(-22’44’’_
2	4,49343(257	-0,00003	-	-

 

Для оцінки похибки приблизного значення  відмітимо, що послідовні наближення (n=0,1,2,…) в силу від’ємності другої похідної монотонна спадає, причому . Тому можна взяти <ξ<, де -   значення з інтервалу (π; ) таке, що f()>0.  Значення легко знайти підбором. Так, наприклад , при n=2, покладемо приблизно =4,49340=arc25727’12’’.  Будемо мати f(=sin257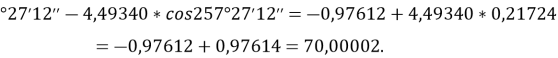

вибрано правильно : 4,49340<ξ<4,49343

 Можна покласти ξ=4,4934, де всі знаки правильні.

Оцінку похибки значення не тяжко провести більш точно. Так як при              х Є похідна спадає і <0, то =׀.

Звідси  ׀ξ-.

Таким чином ξ=4,49343-0,000010, до 0<Ѳ<1.
7) Обчислити з точністю до 0,0005 єдиний додатній корінь  рівняння.

f(x)=.

Розв’язування . Так як f(1)<0 i f(1,1)>0, то корінь знаходиться в інтервалі (1;1,1)

Маємо і =20.  У вибраному інтервалі

, тобто знаки похідних збігаються.

Покладемо і =1,1. Так як f( f(= f(1,1)=0,3105;

(=(1,1)=6,3205,  то  

Тому , що Знайдемо і наступну пару наближень.

Тут , тобто потрібна степінь точності досягнута.

Можна покласти : =  з абсолютною похибкою, меншою

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВИСНОВКИ

        

Під час виконання роботи було ознайомлено та освоєно чисельні методи знаходження коренів рівняння, а саме: метод січних, метод хорд, метод дотичних і інші. При аналізі результатів було виявлено, що при використанні метода дотичних отримуємо найточніші результати.

За допомогою експерименту можна розв'язувати навіть дуже складні задачі, при цьому достовірність результатів тим вища, чим ретельніше відпрацьована методика експе­рименту.

 Якщо можливо  задачу  розв'язати за допомогою рівнянь чи системи рівнянь і розв'язок подати у вигляді за­лежностей, виражених через елементарні та інші відомі функції, то говорять, що знайдено ана­літичний (точний) розв'язок задачі. Однак переважна більшість практично важливих за­дач аналітичних розв'язків не має. До таких належать, на­приклад, задачі будівництва: визначення напружено-деформованого стану пластин, плит, фундаментів; задачі стій­кості, теплопровідності для твердих тіл; напрямленої ди­фузії тощо. У цих випадках використовують чисельні методи, які, оперуючи системою алгебраїчних рівнянь , дають можливість побу­дувати деяку послідовність арифметичних операцій, збіль­шення кількості яких до нескінченності дає точний роз­в'язок. Оскільки на практиці здійснюють скінченне число кроків (операцій), то знайдений розв'язок є наближеним. А через те що обчислювальні операції виконують над чис­лами, то відповідні методи дістали назву чисельних. Най­більшого розвитку чисельні методи набули останнім часом завдяки застосуванню ЕОМ, що мають високу швидкість обчислень і велику ємність оперативної пам'яті. Проте основна роль при цьому відводиться, звичайно, людині, яка повинна вміти сформулювати і поставити задачу, опи­сати її математичними залежностями (створити математич­ну модель об'єкта), скласти алгоритм розв'язання задачі на ЕОМ, написати програму на алгоритмічній мові, зро­зумілій машині, розв'язати задачу й оцінити результати.

Розв'язування багатьох задач зводиться до обчислення  коренів одного нелінійного рівняння або до розв'язання систем нелінійних рівнянь. В обох випадках нелінійні  рівняння,    що   утворюються,   можна   поділити  на два типи — алгебраїчні та трансцендентні.

 Алгебраїчними називають рівняння, що містять лише алгебраїчні функції (цілі, раціональні, ірраціональні).

Нелінійні рівняння, що містять тригонометричні, ло­гарифмічні, показникові, степеневі чи інші спеціальні функції, називають трансцендентними.

Для трансцендентних рівнянь і систем нелінійних рів­нянь прямих методів обчислення коренів не існує. Тому на практиці найчастіше застосовують наближені методи розв'язування цих рівнянь, які дають змогу за допомогою скінченного набору арифметичних операцій обчислити ко­рені будь-якого нелінійного рівняння чи системи неліній­них рівнянь з достатньою точністю. Особливо ефективні наближені методи при реалізації на ЕОМ, оскільки вико­ристовувані для цього алгоритми є простими, зручними, легко програмуються.

 Алгоритм наближеного обчислення коренів неліній­ного рівняння складається з двох етапів.

1.   Відшукування достатньо малих відрізків (інтервалів), у кожному з яких міститься один і тільки один   корінь. Цей етап називають відокремленням коренів (або визначен­ням відрізків ізоляції кореня).

2.  Обчислення   кореня з наперед заданою точністю є, якщо відоме його деяке початкове наближення в інтервалі, що не містить інших коренів. Цей етап називають уточнен­ням наближених значень коренів.

Розв’язування трансцендентних рівнянь сприяє формуванню кмітливості, спостережливості, уваги, розвиває пам'ять і фантазію,вміння логічно мислити, аналізувати, узагальнювати.

Розв’язування запропонованих рівнянь розширює творчі обрії учнів, сприяє глибокому засвоєнню школярами програмного матеріалу. Розвивається мислення і творчі здібності учнів. Формуються нові грані характеру особистості.

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.Віленкін Н. Я., Метод послідовних наближень.-М.:Наука,1981.-203с.

2. Демидович Б. П., Марон І. А. Основи обчислювальної математики. - М.: Наука, 1970. - 664 с.

3. Демидович Б. П., Марон І. А., Шувалова Є. З. Чисельні методи аналізу. - М.: Мир, 1967

4.Ісханов Г. В., Чорний С. М. Чисельні методи.-К.:Вища школа, 1995-375с.

5. Краскевіч В. Є.., Зеленський К. Х., Гречко В. І. Чисельні методи в інженерних

дослідженнях. - К.: Вища шк .., 1986. - 263 с.

6.Лященко М. Я., Головань М. С. Чисельні методи.-К.:Либідь,1996-288с.

7. Ортега Дж., Рейнболдт В. Ітераційні методи розв’язання нелінійних систем рівнянь з багатьма невідомими. - М.: Мир, 1975. - 558 с.

8.Пліс А.І., Слівіна Н.А. Mathcad. Математичний практикум для інженерів та економістів: - М.: Фінанси і статистика, 2003. - 656с.

9.Федак І. В. Готуємось до олімпіади з математики. - Кам’янець-Поділ.: Абетка 2006

10.Ясінський В. А. Задачі математичних олімпіад та методи їх розв’язування. – Т.: Навчальна книга - Богдан,2006.

11.Волков Е. А. Численные методы. – М.:Наука, 1992-257с.