Стаття "Особливості розв’язання геометричних задач за допомогою евристичного мислення"

Левандовська Людмила Федорівна,                

             Геронимівський заклад загальної

             середньої освіти

             І-ІІІ ступенів Черкаської районної ради

             Черкаської області.

В нижче приведеній роботі розглядається один із методів розв’язання задач з геометрії. Саме евристичний метод, на думку автора, вчить учнів мислити, поглиблює розвиток уяви, формує поняття про спільні і відмінні ознаки предметів.

 

Особливості розв’язання геометричних задач

за допомогою евристичного мислення

 

 Протягом  усього свідомого життя людина здобуває  нові знання. Знання – це  сукупність інформації, яку вона дістає з навколишнього світу в процесі суспільно-виробничої практики. Пізнання навколишнього світу людина досягає за допомогою мислення.

Мислення – це процес узагальненого відображення світу: воно дає можливість виділити найістотніші загальні ознаки предметів і утворити загальні поняття про ці предмети. Воно нерозривно пов’язане з мовою. Мова є засобом виділення загально і абстрактного. Німецький філософ Й. Діоген підкреслював, що мислення, як художник, відображає світ, а мова служить для цього художника пензлем, яким він змальовує загальну спорідненість усіх речей.

Одне  з найважливіших завдань, яке ставлю перед собою як учитель – це навчити своїх учнів мислити правильно. Під правильним мисленням треба розуміти таке мислення, яке характеризується:

•            визначеністю і чіткістю;
•            несуперечливістю і послідовністю;
•            обгрунтованістю і доказовістю.

Формувати мислення учнів я починаю  з того що навчаю їх вміння виділяти у предметах властивості. Коли учні навчилися визначати множину різних властивостей, слідуючим кроком є формування поняття про спільні й відмінні ознаки предметів. Навчаю дітей відрізняти в предметах істотні властивості від властивостей неістотних, другорядних.

В даний час у всіх сферах людської життєдіяльності – науці, техніці, народному господарстві – виникають  питання, проблеми нестандартного характеру, вирішення яких часто неможливо здійснити за допомогою стандартних прийомів, методів, що стали вже звичними. Умови життя ставлять всіх нас перед необхідністю повного застосування своїх здібностей і психо-фізичних ресурсів для вирішення складних, нестандартних завдань, що в підсумку призводить до перенапруження, виснаження життєвих сил.                                                                                                                                                                                                                                   З цього приводу відомий психолог XX століття В. Н. Пушкін висловлював свою думку: «Людина повинна зробити деяку сукупність дій, вирішити те чи інше завдання, однак готівку умови не підказують йому способу вирішення цього завдання ... Щоб знайти вихід із такої ситуації, людині необхідно створити нову, що не була у нього раніше стратегію діяльності, тобто здійснити акт творчості ».

У науці давно відомий і до цих пір вдосконалюється такий метод. Назва його - евристичний метод.  Евристична діяльність є «різновидом людського мислення, яка створює нову систему дій або відкриває раніше невідомі закономірності...». Мислення, яке спирається на критерії вибіркового пошуку, завдяки чому з'являється можливість розв’язувати складні, невизначені, проблемні ситуації, називають евристичним. 

Початок евристичного методу деякі бачать у Сократа, який шляхом питань наводив слухача на правильне рішення поставленої проблеми. Він  майстерно використовував бесіду як спосіб знайти істину в суперечці, вчив будувати діалог так, щоб наявні знання людини переводилися з прихованого стану в реальні. Сократ змушував мислити слухача, послідовно підходячи до вирішення ряду більш легких проблем. За слухачем залишалося самостійне мислення, але він рухався не самостійно, його весь час підштовхує вчений. 

До проблем створення евристики зверталися ряд філософів і математиків, наприклад, Р. Декарт, Г. Лейбніц, Б. Больцано, А. Пуанкаре. Наприклад, у праці «Правила для керівництва розуму» Р. Декарт запропонував ряд принципів пошуку істини. Декарт стверджував, що здатність правильно судити і відрізняти істинне від помилкового, що, власне, і іменується здоровим глуздом чи розумом, від природи у всіх людей однакова. «Таким чином, різниця наших думок відбувається не тому, що одні люди розумніше інших, але тільки через те, що ми спрямовуємо наші думки різними шляхами і розглядаємо не ті ж самі речі. Бо мало мати хороший розум, головне - добре його застосовувати».

Евристичне мислення формується орієнтовно до 12-14 років. В порівняння з молодшими учнями, підлітки по-іншому досліджують проблемну ситуацію. В період між 9 і 11 роками дослідницька активність дітей дуже висока. Евристичний метод полягає у взаємодії викладача й учнів на основі створення інформаційно пізнавальної суперечності між теоретично можливим способом вирішення проблеми і неможливістю застосувати його практично, з метою організації самостійної роботи учнів щодо засвоєння частини програми за допомогою проблемно пізнавальних  завдань.

Визначивши рівень складності навчального матеріалу, я як вчитель, вирішую яким  чином його подати  у формі евристичної бесіди, дискусії, поєднуючи часткове пояснення нового матеріалу з постановкою проблемних питань, пізнавальних завдань чи експерименту. Це спонукає учнів до самостійної діяльності, оволодіння прийомами активного мовленнєвого спілкування, постановки й вирішення навчальних проблем. Часто евристичний метод  виступає на практиці у формі так евристичної  бесіди.

Типи евристичних бесід:

•  вхідна (при актуалізації опорних знань);
•  Повідомлююча:

- при вивчені властивостей об’єкта  пізнання, окремих закономірностей явищ;

- при розгляді причин і наслідків тих чи інших явищ;

- при аналізі картини, схеми, ілюстрації;

- при колективному співставленні фактів, явищ;

• завершальна (з метою закріплення або переходу до вивчення нового матеріалу, якщо він є окремим випадком уже вивченого).

Але метод евристичної бесіди неможна вважати універсальним методом.

Сутність евристичного методу навчання полягає у створенні проблемних ситуацій.    Його використовують у випадку значного обсягу в учнів опорних знань та вмінь, необхідних для вирішення навчальної проблеми.                

Наприклад, при вивчені у 8 класі «Подібність трикутників» учні дають відповіді на запитання: Що можна віднести до основних характеристик рівних трикутників? (рівність кутів, сторін, периметрів і площ). Роздивляючись малюнки двох трикутників та виконавши вимірювання, що можна сказати про кути кожної пари трикутників? (відповідні кути кожної пари трикутників рівні), що можна сказати про сторони кожної пари трикутників ? (відповідні сторони кожної пари трикутників пропорційні). Учні самостійно формують означення подібних трикутників.

З огляду на це помітила, що евристика, зокрема, евристичні прийоми, методи надають достатньо сильний вплив на розвиток творчих здібностей, і, що не менш важливо, на розвиток творчого мислення.

Евристичний метод навчання дозволяє  мені  надати учням на уроці більше самостійності і творчого пошуку. Ефективне навчання математики не можливе без використання в навчальному процесі завдань на кмітливість, завдань-жартів, математичних ребусів, софізмів тощо.

Предмет  математики дуже тісно пов'язаний з природними науками. Один з її розділів - геометрія - зародився як природна, емпірична наука.

На уроках геометрії потрібно користуватися найменшою можливістю для того, щоб діти змогли зайнятися творчим пошуком.

1. «Точка —цариця геометрії»

Можна використати цей рисунок для вступної бесіди за геометричним матеріалом у 5 класі («Точка. Пряма лінія») і в 7 класі («Початкові геометричні відомості»)

2. «Чотирикутна колоподібність»

Можна використати під час вивчення геометрії в 8 класі теми «Чотирикутники» і «Вписані й описані чотирикутники». 

Завдання

•  Перелічіть чотирикутники зображені на малюнку, сформулюйте означення кожного; розкажіть, які властивості і ознаки вони мають. (Квадрат, паралелограм, прямокутник, ромб, прямокутна трапеція, рівнобедрена трапеція)
• Що ви знаєте про вписані чотирикутники? Навколо якого чотирикутника можна описати коло? (Прямокутник, квадрат, рівнобедрена трапеція)
• Які чотирикутники називають описаними навколо кола? У які чотирикутники можна вписати коло?  (Ромб, квадрат)

Вважаю важливим прищеплювати новому поколінню евристичні знання, а значить, навчати в школі евристичному мисленню. Найкраще прийоми пошуку вирішення завдань, придатних до будь-яких, у тому числі і «нетиповим, нестандартних завдань», інакше, навчаючи володінню евристичними прийомами (методами) рішення математичних задач.

При викладанні курсу геометрії в загальноосвітній школі доцільним є вивчення і використання евристичних методів розв'язання математичних задач.                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

Головним питанням   при розв’язуванні задачі завжди є план, складання якого спирається на мисленні, евристичних операціях та логіці. Складання плану розв’язування починається з находження евристичних стратегій.       Розв’язок – це  ціль, до якої неможливо прийти відразу, і тому необхідно скласти план як систему можливих дій для досягнення цілі.

Під час пошуку плану розв’язання задачі учням пропоную систему навідних запитань.

Наприклад:

•    прочитайте уважно умову задачі;
•   яку фігуру та які її елементи необхідно накреслити, щоб наочно уявити дані задачі;
•    що потрібно знати, щоб відповісти на запитання задачі;
•    яку додаткову побудову необхідно виконати;
•    чи не можна скористатися певною формулою, ознакою, властивістю, теоремою.

Над використанням методу евристичних запитань працював американський математик Дердьє Пойа. У своїй книзі «Как решать задачу» він зазначав: «Мета системи наставлянь та навідних питань має подвійну суть; перша – допомогти учневі розв’язати саме дану задачу; друга – настільки розвинути здібності учня, щоб у майбутньому він зміг розв’язати задачі самостійно». З його погляду завдання евристики – дослідити способи і методи, які ведуть до відкриття і винаходу.

Евристичний метод найефективніший для навчання розв’язування нетипових задач (система евристичних методів Л.М.Фрідмана). Це метод розбивання задачі на підзадачі.

Метод розбивання задачі на під задачі має три види:

•   розбиття умови задачі на частини;
•   розбиття вимог задачі на частини;
•   розбиття області задачі на частини.

Під час використання цього методу я залучаю учнів до складання плану розв’язування задачі, до розв’язання задач з пропусками, складання пам’яток про розв’язання задач, повторення головних моментів уже розв’язаної задачі, виділення в складній задачі відомих простих, самоперевірки задач за готовим розв’язанням, створення рисунків, схем, таблиць до задач.

Одна з основних навчально-методичних цілей кожного уроку геометрії – формування  вмінь розв’язувати задачі. Для здійснення якої поряд з аналогією, індукцією, дедукцією, порівнянням, узагальненням з учнями на уроках використовуємо аналіз і синтез. Аналіз та синтез  використовуються  як  методи доведення теорем, розв’язання   геометричних задач   на   доведення,  побудову,  обчислення й дослідження. 

Аналіз – від грецького слова analisis – процедура мисленнєвого або практичного розчленування предмета, властивості предмета або відношення між предметами на складові частини.  Часто такий аналіз необхідно зафіксувати, записати, для цього учні будують модель задачі у вигляді  схематичного запису, таблиці, малюнка. Аналіз задачі і побудова   схематичного запису необхідні для того, щоб знайти спосіб розв’язування даної задачі.                                                                              

Процедурою, оберненою до аналізу, є синтез, з яким аналіз часто поєднується в практичній чи пізнавальній діяльності. важливо вміти відокремлювати аналіз та синтез, де це  необхідно,  пам’ятаючи  про те, що аналіз – це шлях до відкриття, а синтез –шлях  до  обґрунтування. 

Синтез – від грецького слова syntesis – об’єднання різних елементів, різнобічних властивостей об’єкта в єдине ціле. Евристичниий метод розв’язування  задачі  направлений на те, як здійснюється пошук способу розв’язку любої задачі. Такий метод розв’язування завжди повинен бути присутній в розв’язку любої задачі: для самої елементарної і тим паче для тієї, яка складніша. Коли спосіб  розв’язування знайдений, необхідно цей спосіб використати до даної задачі, тобто здійснити розв’язок.                                                                                                               

Для учнів   важливо,  порівнюючи,  вміти  розрізняти  властивості  схожих  понять,  щоб   в процесі їх  застосування.   Такими  є,   наприклад,   властивості   прямого   й   прямокутного паралелепіпеда, кута між векторами й прямими.
        Евристичні завдання на порівняння можуть бути такими:
       1.Чим відрізняється об’єкт перший від об’єкту другого?
       2. Яких властивостей немає в першому об’єкті  порівняно з об’єктом другим?
       3. Які додаткові властивості має об’єкт перший порівняно з об’єктом другим?
       4.Чим відрізняються їх формулювання ?

Такі завдання пропоную в процесі вивчення  властивостей чотирикутників:  паралелограма, прямокутника, ромба, квадрата, трапеції (8клас). Виконання  таких  завдань,  формує   вміння   аналізувати,  порівнювати,   запобігає  типовим   помилкам,   коли   учні, формулюючи поняття, називають не всі суттєві  властивості. 
        Можна  використовувати  евристичні  порівняннями  об’єктів,  що  вивчалися на різних уроках,   значно  віддалених  однин   від  одного  за  часом,   наприклад,  з   тем:  «Декартові  координати  на площині»  й  «Декартові  координати  в  просторі», «Вектори на площині» й «Вектори в просторі».
        Аналіз – пошук розв’язання задачі, синтез – саме розв’язання задачі.

 

                                       Аналіз 

   

                                             Синтез

Схема аналітико-синтетичного методу пошуку розв’язання геометричних задач:

•    вибираємо формулу для знаходження шуканої величини;
•    визначаємо, які невідомі величини треба знайти для знаходження шуканої;
•     добираємо відповідні формули для знаходження цих невідомих. 

 Так продовжуємо до тих пір, доки всі невідомі величини не будуть виражені через відомі. Для розв’язання задачі достатньо здійснити зворотній перехід від останньої дії до першої.

Наприклад.

Задача. З вершини К прямокутника КРСЕ провели перпендикуляр КD до його площини, відстані від точки D до інших вершин дорівнюють 6м, 7м та 9м. Знайти довжину перпендикуляра КD.

Розв’язання

Виконуємо побудову рисунка, тобто переходимо від абстрактної форми до конкретної.

 

 

 

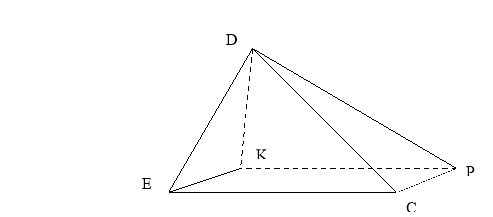
 Розчленовуємо умову  задачі:

•     Де розміщена найбільша похила? (DС=9м);
•     DЕ = 6м; DР = 7м.
•     Що буде, якщо 6м і 7м поміняємо місцями? Як це вплине на розв’язок задачі?                  

Аналіз:

 

 

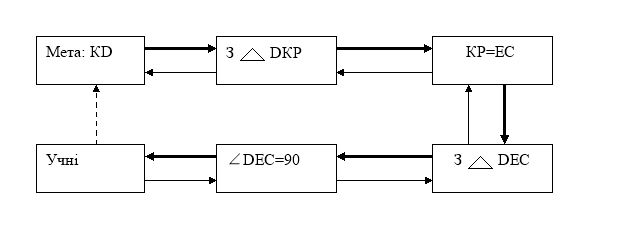
Під час виконання етапів розв’язування задачі учень повинен відповісти на наступні запитання:

• Що невідомо?
• Що дано? 
• Яка умова задачі?
• Чи зустрічалась раніше така задача?
• Чи розв’язували подібну задачу?
•  Чи можна нею скористуватися?                                                                                                                                                                                                           

Отже, учитель, який навчає учнів   розв’язувати  задачі, повинен визвати у них інтерес до задачі, переконати, що від математичної  задачі можна отримати задоволення, як від розгадування кросвордів. Задачі, які учні розв’язують на уроці  не дуже важкі. При розв’язанні нескладних задач  учні  багато часу витрачають на судження про те з чого починати, особливо в 7, 8 класах. Вчителю потрібно допомогти учневі знайти шлях до розв’язку задачі. Це дозволить йому розвивати математичні здібності, накопичувати досвід, який в подальшому допоможе знаходити шлях до розв’язання нових задач.

Цінність евристичних уроків з геометрії полягає в тому, що учні самостійно здобувають нові знання, вчаться їх застосовувати виходячи із досвіду, вчитель лише підводить їх  до правильного розв’язку.    Евристичне навчання  на уроках геометрії допомагає формувати свою точку зору , позицію.                                                                                                                                                           

Але у евристичного методу розв’язування задач є недолік – застосування  цього методу залежить від рівня навченості і розвитку учнів.

Завдання мене, як учителя, залучити  учнів до творчої діяльності, допомогти їм розкрити свої здібності; розвинути в них  потребу у творчій діяльності, прагнення до самостійного здобування знань. Усе це свідчить про присутність у математичній діяльності евристичної компоненти.

Необхідно і дальші розробляти і удосконалювати види і методи евристичного навчання на уроках геометрії.

           
         Список літератури:

1.  Кулюткин Ю.К., Эвристические методы в структуре решений, М.: Педагогика, 1970

2.   Пойа Д. Как решать задачу. – Львов: журнал “Квантор”,1991.

3. Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Книга для учащихся старших классов средней школы. – М.: Просвещение, 1989.

4. Скафа Е.И. Евристичні методи   при формуванні  математичних понять / Е.И. Скафа // Дидактика математики: проблеми і дослідження: міжнар. зб. наук. робіт. - Донецьк: Фірма ТЕАН, 2001. - Вип. 15. - С. 68-80.

5. Заесенок В. П. Евристичні прийоми вирішення логічних завдань / / Математика в школі. - 2005. - N 3. 

6. І.А.Гарнагіна Як навчити розвязувати задачі . Математика в школі. - 2008. - N 27. 

 7. Л.В.Колеснікова. Нестандартні задачі – шлях до розвитку творчого мислення учнів. Математика в школі. - 2008. - N 8-9. 

 8. В.К.Борисова .Аналіз і синтез пошуку  розв’язання геометричних задач. Математика в школі. - 2006. - N 2.  Начало формыКонец формы