Тема: Невизначений інтеграл. Основні властивості та обчислення інтеграла

Мета:

Навчальна: працювати над закріпленням понять: первісна функції на заданому проміжку, основна властивість первісної, невизначений інтеграл; засвоєнням відповідної символіки; продовжити формуванню вмінь учнями розв’язувати завдання на доведення того, що деяка функція є первісною для поданої, а також знаходити загальний вигляд первісної для функції.

Розвиваюча: розвивати вміння математичною мовою висловлювати власну думку; правильно користуватись термінологією, пов’язаною з вивченою темою;

Виховна: виховувати наполегливість; вміння робити правильні висновки та бачити кінцеву мету;

Компетенції:

Математична компетентність:

Уміння: оперувати числовою інформацією; прогнозувати в контексті навчальних та практичних задач;

Навчальні ресурси: розв’язування математичних задач;

Тип уроку: засвоєння знань, формування умінь;

Обладнання: опорний конспект, навчальна презентація, мультимедійне обладнання; технологічна карта заняття, таблиця «Первісна та інтеграл»

Література.

[2] Істер О.С. Математика: (алгебра і початки аналізу та геометрія, рівень стандарту) : підруч. для 11-го кл. закл. заг. серед. освіти/ Александр Істер. Київ: Генеза, 2019, 304 с.

 

Хід заняття

1. Організаційний етап

• Привітання.
• Перевірка присутніх на занятті.
• Налаштування на роботу.

 

2. Перевірка домашнього завдання

Перевірка домашнього завдання у вигляді взаємоперевірки та вибіркової перевірки зошитів учнів.

Проведемо гру «Вірю-не вірю»:

1. Чи правильно, що якщо функція F(x) – первісна для функції ƒ(x), то і функція F(x) +1 і F(x) +100 є первісними для функції ƒ(x)?
2. Чи правильно, що функція F(x) є первісною для функції ƒ(x), якщо:

а) б)

в) г)

ґ) д)

 

 

 

3. Знайомство з темою та метою уроку

Мета нашого уроку: закріпити вивчені на попередньому занятті поняття та відпрацювати навички їх застосування при знаходженні невизначеного інтегралу.

 

4. Актуалізація опорних знань і вмінь

 Перевірка теорії:

1.  Що називають диференціюванням функції?

2   Як називають операцію, обернену до диференціювання?

3   Що називають первісною функції?

4   Чому дорівнює первісна одночлена axⁿ?

5   Сформулюйте теорему про первісну суми двох функцій.

6. Що називають невизначеним інтегралом?

7. Як називають функцію ƒ(x), а вираз ƒ(x)dx?

 

Перевірка вивчення таблиці первісних та інтегралів

 

Вправа 1. Виконайте усно: Знайдіть первісну функції.

1)  f(x) = x⁹;  2)  f(x) = x;   в)  f(x) = x³; г)  f(x) = x^0,5; 4)  f(x) = sin x; 5)  f(x) = 5; 6)  f(x) = 0; 

7)  f(x) = cos x; 8)  f(x) = 0,5x;  9)  f(x) = x–2; 10)  f(x) = e^x;   11)  f(x) = –0,1.

2) Вправа. Поясніть, як перевірити, що функція F(x) є первісною для функції ƒ(x) на вказаному проміжку?

1. 
2. 
3. 
4. 

 

5. Закріплення знань і вмінь.

1) Математичний марафон. При розв’язанні вправи вказувати формулу або правило, яке застосовується.

Колективно у дошки ланцюжком:

Знайдіть загальний вигляд первісних для функції:

№ 9.7. 1) 2)3) 4)

№ 9.9. 1) 2)3) 4)

 

Знайдіть невизначений інтеграл:

 № 9.11.

Для функції ƒ(x) знайдіть первісну F(x), що набуває заданого значення в точці:

№ 9.13. 1) 2)

Для заданої функції ƒ(x) знайдіть первісну F(x), графік якої проходить через точку М:

№ 9.15. 1) 2)

Робота в парі.

№ 1. Перевірте, чи правильні рівності?

№ 2. Установіть відповідність між функцією (1-4) та її первісною (А-Д).

1			А
2			Б
3			В
4			Г
Відповідь: 1Б 2А 3Г 4В			Д

 

6. Підведення підсумків уроку

 

7. Повідомлення домашнього завдання

[2], Розділ 2, §§ 8, 9, таблицю інтегралів вивчити напам’ять, виконати вправи
№№ 9.8, 9.10, 9.14, 9.16 с. 87

Знайдіть загальний вигляд первісних для функції:

№ 9.8. 1) 2)3) 4)

№ 9.10. 1) 2)3)

 4)

Для функції ƒ(x) знайдіть первісну F(x), що набуває заданого значення в точці:

№ 9.14. 1) 2)

Для заданої функції ƒ(x) знайдіть первісну F(x), графік якої проходить через точку N:

№ 9.16. 1) 2)

 

 

 

 

 

 

 

 

 

Опорний конспект

ПЕРВІСНА

 

 

 

 

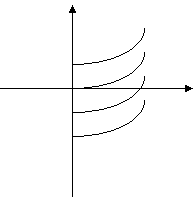Первісною f(x) на заданому проміжку Х  називається функція F(x):

 F (x) = f(x) для всіх хХ

                                                                                                                                                                                 

 

 

 

                                                                                                             С=const                                                                                                                                                                                                             

 

 

Функція	Первісна
x, -1
	ln x + C
ex	ex+C
sin x	- cos x + C
cos x	sin x + C
(kx + b), -1, k0
sin(kx+b), k0	- cos(kx+b) + C
cos(kx+b), k0	sin(kx+b)
ax
	tgx
	-ctgx

Правила інтегрування

                                                             ,      k=const        

 

                                                                                                                                                                                                                                                                                 

 

Означення: сукупність (множина) всіх первісних для функції ƒ(x) називають невизначеним інтегралом функції ƒ(x)
Невизначений інтеграл позначають як або , ,