урок теоретичного навчання

Про матеріал

Урок теоретичного навчання призначений для учнів професійно технічних навчальних закладів

Перегляд файлу

Державний навчальний заклад «Лісоводський професійний аграрний ліцей»

Конспект уроку з математики на тему: «Многогранники»

Розробила: викладачка

математики Повх Л.М.

Тема уроку: «Многогранники».

Тип уроку: урок – проєкт.

Група поділена на три підгрупи, кожна з яких отримала тему проєкту. Працюючи над проєктом більше двох тижнів, 3 підгрупи по конкретній темі самостійно працювали з великим обсягом інформації, вивчили, проаналізували й узагальнили теоретичний матеріал, який нам стане в нагоді для вирішення завдань поданої теми.

Присутнім на уроці викладачам було запропоновано бути незалежними експертами, які отримали бланки для оцінювання

Бланк – оцінювання проєктів

	*Формулюван-* *ня мети*	*Відповідність інформації*	*Логічність і послідовність*	*Грамотність*	*Привабливість слайдів*	*Підсумкова оцінка*
*І група*
*ІІ група*
*ІІІ група*

В кінці уроку експерти оцінили та проаналізували роботу груп.

Мета:

розширити уявлення про опуклі многогранники, ознайомитися з їх деякими властивостями, формувати поняття правильних і напівправильних багатогранників, показати зв'язок математики з життям;
формування компетентності у сфері самостійної пізнавальної діяльності, навичок самостійної роботи з великим обсягом інформації, формування навичок роботи в команді, розвиток творчих здібностей особистості;
продовжити виховання в учнів шанобливого ставлення один до одного, почуття товариства, культури спілкування, почуття відповідальності, виховувати культуру ділового спілкування.

Обладнання: мультимедійний проєктор, ноутбук моделі багатогранників.

Хід уроку:

1 етап – організаційний

Викладач: У програмі з геометрії є особливі теми, які чекаєш з нетерпінням, передчуваючи зустріч з неймовірно красивим матеріалом. До таких тем можна віднести тему " Многогранники" або «Багатогранники». Тут не тільки відкривається дивовижний світ геометричних тіл, які мають неповторні властивості, а й цікаві наукові гіпотези. Жодні геометричні тіла не мають такої досконалості і краси, як правильні багатогранники. Сьогодні на уроці ми дізнаємося і побачимо багато цікавого, нам належить відповісти на такі питання, як, наприклад:

Які багатогранники називаються правильними? Скільки їх існує? Що таке ейлерова характеристика? І багато-багато інших ... І, нарешті: де, навіщо і для чого нам потрібні багатогранники? Може, можливо, в житті можна обійтися і без них?

Отже, я запрошую вас у "Світ многогранників".

Мені хотілося б почати зі слів Бертрана Рассела: «Математика володіє не тільки істиною, але і вищою красою - красою відточеною і строгою, піднесено чистою і прагне до справжньої досконалості, яка властива лише найбільшим зразкам мистецтва»

2 етап – представлення проєкту (виступ груп з презентацією щодо звіту своєї дослідницької роботи, ознайомлення з отриманими результати та підведення підсумків )

• Виступ 1-ї групи «Поняття многогранника. Формула Ейлера для опуклих многогранників».

Наша група працювала над проєктом «Поняття многогранника. Формула Ейлера для опуклих многогранників».

Метою проєкту був збір необхідних даних для узагальнення поняття многогранника, їх аналіз та ознайомлення з їх змістом одногрупників.

Многогранники є опуклі та не опуклі.

Многогранник називається опуклим, якщо він розташований по один бік від площини кожної його грані.

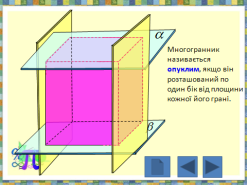
Неопуклий многогранник

Завдання1: Учням з 2,3 груп, експертам пропонується :

На малюнку знайдіть опуклі та не опуклі многогранники.

2-га група – перша стрічка

3-тя – друга;

Експерти – третя.

Перевіримо результати.

Формула Ейлера для опуклих многогранників

Перевіримо виконання формули Ейлера для деяких многогранників.

Завдання2

Учням з 2,3 груп, експертам пропонується :

підрахувати число вершин, граней і ребер деяких моделей багатогранників: трикутної і чотирикутної пірамід, трикутної і чотирикутної призм. Потім занести ці дані в таблицю.

Група 2 виконує перевірку формули Ейлера для трикутної піраміди;

група 3 виконує перевірку формули Ейлера для чотирикутної піраміди;

експерти виконують перевірку формули Ейлера для трикутної призми.

Назва багатогранника	В	Г	Р
Трикутна піраміда	4	4	6
Чотирикутна піраміда	5	5	8
Трикутна призма	6	5	9

Звіт груп, експертів.

Висновок

Виступ 2-ї групи «Правильні і напівправильні многогранники".

Наша група працювала над проєктом «Правильні і напівправильні багатогранники".

Метою проєкту був збір необхідної інформації для розширення знань про правильні многогранники та знайомство з напівправильними многогранниками.

Ми починаємо знайомство з правильних плоских і просторових фігур. Назва "правильні" йде від античних часів, коли прагнули знайти гармонію, правильність, досконалість в природі і людині.

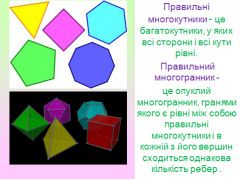
Правильні многокутники - це багатокутники, у яких всі сторони і всі кути рівні, правильні багатогранники - це опуклий многогранник, гранями якого є рівні між собою правильні многокутники і в кожній з його вершин сходиться однакова кількість ребер.

До цих пір багатокутники нерідко називають у науці по-грецьки з закінченням "гон":

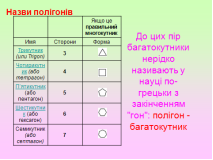
Кожен з вас знайомий з найпростішими просторовими математичними фігурами, або многогранниками. По-грецьки вони закінчуються на "едр".

Отже правильні многогранники

мають назви

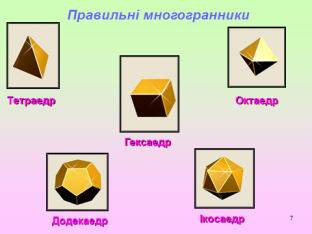
Всі правильні багатогранники були відомі ще у Стародавній Греції, і їм присвячена заключна, 13-а книга знаменитих "Начал" Евкліда. Ці багатогранники часто називають також Платоновим тілами - в ідеалістичної картині світу, даної великим давньогрецьким мислителем Платоном, чотири з них уособлювали 4 стихії: тетраедр - вогонь, куб –

землю, ікосаедр - воду, октаедр - повітря, п'ятий же багатогранник, додекаедр, символізував світобудову - його по-латині стали називати quinta essentia (квінта есенція), що означає все найголовніше, основне, істинну сутність чого-небудь.

Крім правильних многогранників, є напівправильні многогранники. Тринадцять вперше відкрив і описав Архімед - це тіла Архімеда. Вони відрізняються від Платонових тіл тим, що їх грані - правильні багатокутники декількох типів.

Кеплер першим опублікував повний список тринадцяти Архімедових тіл і дав їм ті назви, під якими вони відомі понині.

Увага! Запитання.

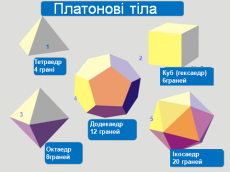
Як називаються тіла зображені на малюнку?

Дайте назву зображеним фігурам,та вкажіть число їх граней?- І група.

Вкажіть Платонові тіла та тіла Архімеда. – 2 група.

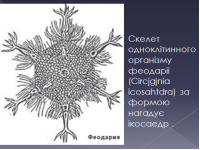
Виступ 3 групи « Многогранники в житті, в мистецтві, в природі, в архітектурі, побуті тощо».

Наша група працювала над проектом «Многогранники в житті, в мистецтві, в природі, в архітектурі, , побуті тощо». Мета з’ясувати де ми зустрічаємося з многогранниками.

3 етап - підсумкове обговорення-

Підведення підсумків.

Висновки:

• Ні одні геометричні тіла не мають такої досконалості і краси як багатогранники.

• Існує тільки 5 правильних багатогранників (тіл Платона), 13 напівправильні багатогранники, відкритих Архімедом, нескінченні серії напівправильних багатогранників, 4 типи правильних зірчастих багатогранників.

• Многогранники оточують нас всюди: у природі, архітектурі, мистецтві, техніці, побуті тощо.