Тема уроку "Квадратична функція"

                           Урок  алгебри (9клас)

 

Тема: Квадратична функція.

Алгебра: підруч. для 9 кл.  загальноосвіт.  навч.  закл. / В.Р. Кравчук, М.В. Підручна, Г.М. Янченко, -Тернопіль: Підручники і посібники, 2017.

Мета: на основі соціального досвіду учнів розширити  та поглибити знання  про функцію, скласти алгоритм дослідження та побудови графіка квадратичної функції;

  розвивати критичне мислення, творчу активність, уміння аналізувати, порівнювати, співставляти, робити висновки та обґрунтовувати їх, комунікативні здібності;

 виховувати культуру математичного письма та побудов, наполегливість у процесі навчальної діяльності.

Тип уроку: урок засвоєння нових знань.

Технічне обладнання та програмне забезпечення:  презентація мультимедійна система.

 

Хід уроку

І. Психологічне  налаштування   учнів.

ІІ. Перевірка виконання домашнього завдання.

- Учні усно вказують хід розв’язання завдань з рівня А;

- Завдання рівня Б коментують з детальним поясненням моментів, які викликали труднощі при виконанні і подальшим записом у зошитах;

- завдання рівня В коментують біля дошки з необхідними короткими записами.

ІІІ. Мотивація навчальної діяльності.

Тема, вивчення якої триває, містить багато підтем, багато важливих понять. На сьогоднішньому уроці перед нами стоїть завдання – поглибити  та розширити знання про функцію. А основне, дати відповідь на запитання – матеріал що вивчатиметься сьогодні цілком новий, чи майже відомий?

 

ІІІ. Актуалізація опорних знань та удосконалення вмінь і навичок.

Завдання 1.

а)  повторити загальні відомості про функцію. Прийом «Кластер»

 

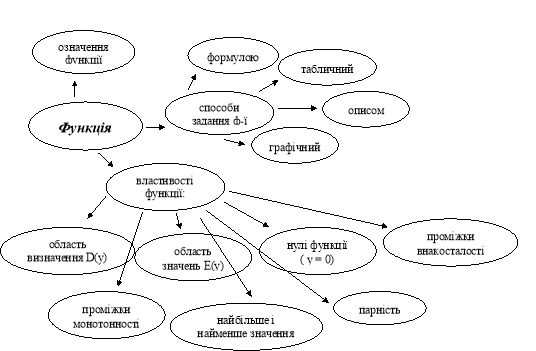
б) використовуючи слайд 1, сформулювати всі властивості функції, графік якої  зображений на малюнку.

в) за графіком визначити, чому дорівнює значення функції в точці х = 3,  х = –1.

г) для якого аргументу значення функції дорівнює   –4.

                                                                                 Слайд1.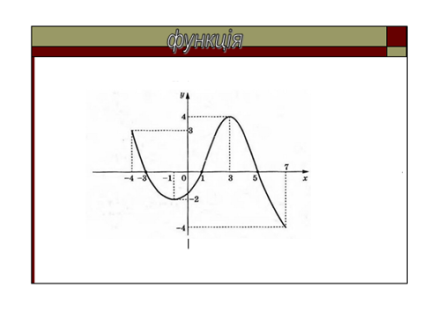                                                                                                                                                                                                                                                                  

Завдання 2.    

а) сформулювати правила, за якими із графіка функції                   можна

отримати графіки функцій:                                                                                                                     

1)                                                  ;

2)                                                   ;

3. ;
4. ;
5. ;
6. ;

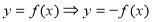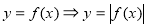
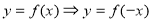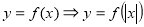                               слайд 2.

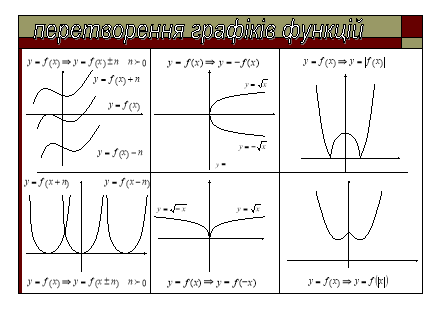
(після кожного сформульованого правила, відкривається відповідний малюнок слайду2, зображення залишається на екрані і під час виконання практичних завдань).

б) які перетворення графіків, відомі вам, не вказані?    

    (                                                                   )

в) використовуючи перетворення графіків, побудувати графік функції      

                    у =(х – 3)²+ 1.

          Розв’язання:

1. будуємо графік функції   у =х² .        .

2. будуємо графік функції у =(х – 3)², перемістивши графік функції   

     у =х²  на 3 одиниці вправо.

3. будуємо графік функції у =(х – 3)² +1, перемістивши графік функції

у =(х – 3)²  на 5 одиниці вгору.

 

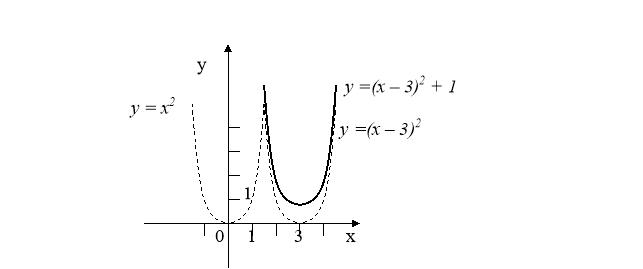
г) за графіком записати властивості функції:

 1. D(у): х є (-∞;+∞);

2. Е(у): у є [1;+ ∞);

3. функція спадає при х є (- ∞; 3];

4. функція зростає при х є [3; +∞);

5. функція не має нулів;

6. у ˃ 0 при х є (-∞;+∞);

7. найменше значення функції у = 1 при х = 3.

д) подати праву частину формули у =(х – 3)²+ 1   у вигляді квадратного тричлена. ().  Побудований графік і обидві формули залишаються на дошці.

 

ІV. Сприймання нового матеріалу.

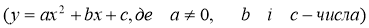1. Означення квадратичної функції.

 

Після сформульованого вчителем означення учні роблять висновок про рівень обізнаності у даній темі і беруть активну участь у подальшому її опрацюванні:

•  Що є графіком квадратичної функції? (парабола)
• Як побудувати графік квадратичної функції?

(виділити квадрат двочлена із квадратного тричлена та використати для побудови перетворення графіків функцій) - бажано щоб це озвучили учні.

• Чи можна визначити  координати вершини параболи , маючи загальний вигляд квадратичної функції?(використовуючи побудований графік та співставляючи дві формули учні роблять висновок про можливий варіант знаходження координат вершини параболи)

 

2. Виведення формул для обчислення координат вершини:

 

 

 

 

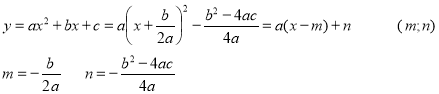
3. Побудова графіка квадратичної функції:

         І спосіб:  виділити квадрат двочлена із квадратного тричлена та використати для побудови перетворення графіків функцій.

        ІІ спосіб:  алгоритм дослідження квадратичної функції для побудови її графіка:

 

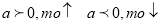1. Координати   вершини  (m; n)                                     ;
2. Напрям віток:                                       ;
3. Точки перетину з віссю ОУ (х = 0);
4. Точки перетину з віссю ОХ (у = 0);
5.  Додаткові точки(при необхідності).

 

4. Властивості функції. (учні роблять висновок, що цей матеріал вже відомий). Для узагальнення використовуємо слайд.

                                                                    слайд 3

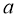5. Розміщення графіка в залежності від знаку дискримінанта та знаку коефіцієнта      .                                                  ( слайд 4)    

   

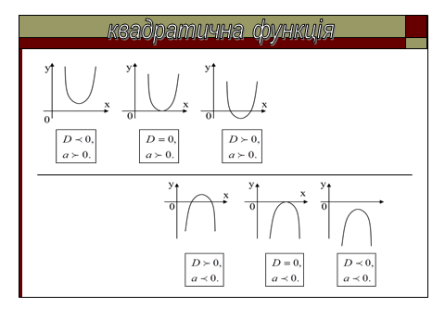
Використовуючи слайд 4, учні розглядають всі можливі випадки розміщення графіка квадратичної функції(обовязково вказуючи причини такого розміщення)                                                                                                                         

V. Формування навиків.

1.   розв’язати колективно:

 Побудувати графік функції у = – х² – 6х – 5. Користуючись графіком, знайти:

1. множину значень функції;
2. проміжок, на якому функція спадає;
3. множину розв’язків нерівності   – х² – 6х – 5 ≤ 0 .

Розв’язання:

Графіком функції у = – х² – 6х – 5 є парабола, вітки якої напрямлені вниз оскільки  (а = -1).

 Координати вершини параболи: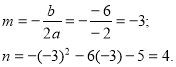
 

(-3; 4)

З віссю ОХ графік перетинається в точках:

– х² – 6х – 5 = 0;

 х² + 6х + 5 = 0;

 х₁ = -5;  х₂ = -1.

(-1; 0) і (-5; 0).

 З віссю ОУ графік перетинається в точці (0; -5).

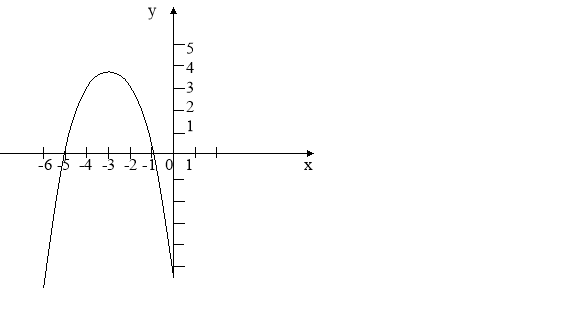
1. Е(у): у є (-∞; 4].

2. функція спадає при х є [-3; ∞).

3. – х² – 6х – 5 ≤ 0 при х є (- ∞; -5] U [-1; ∞).

 

VІ. Підведення підсумків. Рефлексія.

1. Було цікаво…
2. Я зрозумів, що…
3. Я навчився…
4. Було важко…
5. Мене здивувало…
6. Тепер я зможу…

 

 Домашнє завдання.    Опрацювати п. 12. Розв’язати : № 457,  №464

 

 

                             Розробила учитель математики  Підгорна М.М.