Тематичне оцінювання з математики. 7 клас.
Тематичне
оцінювання
з математики
7 клас
7 клас (алгебра)
ТО №1. “Рівняння.”
І варіант
І рівень
1) Розв'язати рівняння х + 25 = 49.
2) Чи рівносильні рівняння
у – 7 = 21 і 2у – 1 = 55 ?
3) Чи мас корені рівняння 5х + 4 = 5х + 6?
ІІ рівень
4) Знайти корені рівняння: а) – 7х = 14;
б) 6х – 14 = 3х +16; в) 10 – (5х – 3 ) = 3х + 17.
ІІІ рівень
5) Розв'язати рівняння 6 – 4·(2х – 5) = 3·(4 – 2х).
6) Частину дороги в школу Галя їде на автобусі, а решту дороги проходить пішки. На всю дорогу вона витрачає 26 хвилин. Вона іде на 6 хвилин довше, ніж їде на автобусі. Скільки хвилин вона їде на автобусі?
IV рівень
7) Теплохід пройшов відстань між пристанями за течією за 4 год., а в протилежному напрямку - за 5 год. Яка власна швидкість теплохода, якщо швидкість річки 2,3 км/год?
ІІ варіант
І рівень
1) Розв'язати рівняння х – 12 = 50.
2) Чи рівносильні рівняння
у + 9 = 29 і 2у + 4 = 44 ?
3) Чи має корені рівняння 6х – 2 = 6х + 8?
ІІ рівень
4) Знайти корені рівняння: а) 9х = –18 ;
б)20 – 5х = 2х – 15; в) 8х – (6х – 4) = 64 – 4х.
ІІІ рівень
5) Розв'язати рівняння 5·(2х – 3) = 3 – 3·(3 – 2х).
6) Турист подолав 600 км. Частину дорога пролетів літаком, а решту – проїхав автобусом. На літаку пролетів на 480 км більше, ніж автобусом. Скільки кілометрів проїхав турист автобусом?
IV рівень
7) За 9 год теплохід, проходить за течією річки такий самий шлях, як за 11 год проти течії. Знайдіть власну швидкість теплохода, якщо швидкість течії річки 2 км/год?
ІІІ варіант
І рівень
1) Розв'язати рівняння х + 60 = 85.
2) Чи рівносильні рівняння
у – 12 = 18 і 3у – 3 = 87 ?
3) Чи має корені рівняння 7х + 8 = 7х + 10?
ІІ рівень
4) Знайти корені рівняння: а) –10х = 40;
б)14 – 3х = 20 – 5х; в) 12х – (х – 4) = 3х + 84.
ІІІ рівень
5} Розв'язати рівняння 6·(3х – 7) = 6 – 3·(4 – 2х).
6) У двох альбомах було 113 марок. В першому альбомі на 23 марки менше, ніж в другому. Скільки марок в кожному альбомі?
IV рівень
7) За 10 год проти течії річки катер проходить на 3О км більше, ніж за 5 год за течією. Яка швидкість течії річки, якщо власна швидкість катера 15 км/год?
IV варіант
І рівень
1) Розв'язати рівняння х – 24 = 15.
2) Чи рівносильні рівняння
у + 20 = 30 і 5у + 5 = 55 ?
3) Чи має корені рівняння 8х – 5=8х +15?
ІІ рівень
4) Знайти корені рівняння: а) 5х = – 25;
б)16 + 10х = 5х – 14; в)2х – (х + 8) = 12 – 3х.
ІІІ рівень
5) Розв'язати рівняння:
5·(3х – 2) = 12 – 2·(6 – 5х).
6) У двох акваріумах 193 риби. В одному акваріумі на 53 риби менше, ніж в другому. Скільки риб в кожному акваріумі?
IV рівень
7) За 8 год проти течії річки катер проходить на 2 км більше, ніж за 6 год за течією. Яка власна швидкість катера, якщо швидкість течії річки 3 км/год?
ТО № 2: “Одночлени.”
І варіант
І рівень
- Знайти значення виразу 102 + 6·( – 5)2
- Обчисліть значення одночлена 5а2b3 , якщо а = 3, b = 2.
ІІ рівень
- Подайте вираз у вигляді одночлена, стандартного вигляду
а) 4х2у2·2ху; б) – 3а5b4·(– 2а2b5)
ІІІ рівень
4) Виконайте множення одночленів
а) – 10ху·(–2х2у3); б) 2,5а2b1О·2a6b8.
5) Виконайте піднесення одночлена до степеня
а) (2х5у2)3; б) (3a6b9)2.
ІV рівень
6) Спростіть вирази:
а) ![]() ; б)
; б) ![]() .
.
II варіант
І рівень
1) Знайти значення виразу 222 – 6·( – 4)2
2) Обчисліть значення одночлена 6а3b2 , якщо а = 2, b = 3.
ІІ рівень
- Подайте вираз у вигляді одночлена, стандартного вигляду
а) 0,4х3у5·5ху4; б) – 3аb·(– 2а6b5)
ІІІ рівень
4) Виконайте множення одночленів
а) – 2,5ху2·(–2х4у5); б) ![]() а2b7·4ab6.
а2b7·4ab6.
5) Виконайте піднесення одночлена до степеня
а) (2,1х2у6)2; б) (![]() ab8)3.
ab8)3.
ІV рівень
6) Спростіть вирази:
а) ![]() ·100
·100![]() ; б)
; б) ![]() .
.
ІІІ варіант
І рівень
- Знайти значення виразу 12·( – 3)3 – 192.
- Обчисліть значення одночлена 10а2b , якщо а = – 3, b = 5.
ІІ рівень
- Подайте вираз у вигляді одночлена, стандартного вигляду
а) –5х10у2·(-2,6ху5); б) – 2аb·(– ![]() а2b5)
а2b5)
ІІІ рівень
4) Виконайте множення одночленів
а) 7,8х5у6·(–5ху2); б) ![]() а4b6·(-18a5b).
а4b6·(-18a5b).
5) Виконайте піднесення одночлена до степеня
а) (–9,4ху9)2; б) (![]() a9b3)3.
a9b3)3.
ІV рівень
6) Спростіть вирази:
а) ![]() ; б)
; б) ![]() .
.
IV варіант
І рівень
1) Знайти значення виразу 6·(-5)2 + 17 2
2) Обчисліть значення одночлена 2а2b4 , якщо а = 5, b = –1.
ІІ рівень
3) Подайте вираз у вигляді одночлена, стандартного вигляду
а) 4х2у10·(–0,7ху); б) –2,4а5b6·(– 2а4b)
ІІІ рівень
4) Виконайте множення одночленів
а) – 2,5ху9·(–5х5у); б) ![]() а5b4·(–16ab).
а5b4·(–16ab).
5) Виконайте піднесення одночлена до степеня
а) (–5,8х8у7)2; б) (![]() a5b10)3.
a5b10)3.
ІV рівень
6) Спростіть вирази:
а) ![]() ·32
·32![]() ; б)
; б) ![]() .
.
ТО № 3: “Многочлени”.
І варіант
І рівень
1) Що таке многочлен?
2) Зведіть подібні доданки ![]() .
.
3) Виконайте додавання многочленів
![]() .
.
ІІ рівень
4) Виконайте множення
а) ![]() ; б)
; б) ![]() .
.
5) Розв'яжіть рівняння ![]() .
.
ІІІ рівень
6) Спростити вирази:
а) ![]() ;
;
б) ![]() .
.
7) Знайти корінь рівняння
![]() .
.
IV рівень
8) Доведіть, що вираз
![]()
при будь-якому ![]() набуває одного значення.
набуває одного значення.
9) Перевірте, чи значення виразу
![]() діліться на 6.
діліться на 6.
ІІ варіант
І рівень
І) Як додати і відняти многочлени?
2) Зведіть подібні доданки ![]() .
.
3) Виконайте додавання многочленів
![]() .
.
ІІ рівень
4) Виконайте множення
а) ![]() ; б)
; б) ![]() .
.
5) Розв'яжіть рівняння ![]() .
.
ІІІ рівень
6) Спростити вирази:
а) ![]() ;
;
б) ![]() .
.
7) Знайти корінь рівняння
![]() .
.
IV рівень
8) Доведіть, що вираз
![]()
не залежить від ![]() .
.
9) Перевірте, чи значення виразу
![]() діліться на 7.
діліться на 7.
ІІІ варіант
І рівень
І) Як помножити одночлен на многочлен?
2) Зведіть подібні доданки ![]() .
.
3) Виконайте додавання многочленів
![]() .
.
ІІ рівень
4) Виконайте множення
а) ![]() ; б)
; б) ![]() .
.
5) Розв'яжіть рівняння ![]() .
.
ІІІ рівень
6) Спростити вирази:
а) ![]() ;
;
б) ![]() .
.
7) Знайти корінь рівняння
![]() .
.
IV рівень
8) Доведіть, що вираз
![]()
дорівнює нулю.
9) Перевірте, чи значення виразу
![]() діліться на 6.
діліться на 6.
ІV варіант
І рівень
І) Як помножити многочлен на многочлен?
2) Зведіть подібні доданки ![]() .
.
3) Виконайте додавання многочленів
![]() .
.
ІІ рівень
4) Виконайте множення
а) ![]() ; б)
; б) ![]() .
.
5) Розв'яжіть рівняння ![]() .
.
- 54 -
ІІІ рівень
6) Спростити вирази:
а) ![]() ;
;
б) ![]() .
.
7) Знайти корінь рівняння
![]() .
.
IV рівень
8) Доведіть, що вираз ![]()
набуває від’ємних значень при будь-якому![]() .
.
9) Перевірте, чи значення виразу
![]() діліться на 12.
діліться на 12.
ТО № 4. “Формули скороченого множення. Цілі вирази”. (Підсумкова за І семестр).
І варіант
І рівень
1) Сформулюйте правило піднесення одночлена до степеня?
2) Як віднімають многочлени?
3) Запишіть формулу квадрату суми двох виразів і
сформулюйте її словами?
ІІ рівень
4) Зведіть подібні члени многочлена:
![]() .
.
5) Виконайте множення: ![]()
6) Піднесіть вираз ![]() до квадрата.
до квадрата.
ІІІ рівень
7) Розкрийте дужки: ![]() .
.
8) Спростіть вираз:
![]() .
.
9) Розв'яжіть рівняння:
![]() .
.
IV рівень
10) Доведіть, що значення виразу не залежить від![]() :
:
![]() .
.
11) Перевірте чи значення виразу
![]() ділиться на 6.
ділиться на 6.
ІІ варіант
І рівень
1) За яким правилом підносяться степені до степенів?
2) Що таке многочлен?
3) Сформулюйте правило множення многочленів?
ІІ рівень
4) Зведіть подібні члени многочлена:
![]() .
.
5) Виконайте множення: ![]()
6) Піднесіть вираз ![]() до квадрата.
до квадрата.
ІІІ рівень
7) Розкрийте дужки: ![]() .
.
8) Спростіть вираз:
![]() .
.
9) Розв'яжіть рівняння:
![]() .
.
IV рівень
10) Доведіть, що значення виразу не залежить від![]() :
:
![]() .
.
11) Перевірте чи значення виразу
![]() ділиться на 7.
ділиться на 7.
ТО № 5: “Розкладання многочленів на множники”.
І варіант
I рівень
-
Винести спільний множник за дужки:
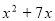 .
.
- 56 -
-
Розкласти
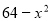 на множники за формулою
на множники за формулою
![]() .
.
-
Розкласти
 на множники за формулою
на множники за формулою
![]() .
.
II рівень
-
Розв'язати рівняння
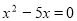 .
.
- Обчислити найзручнішим способом:
а)![]() ; б)
; б) ![]() .
.
III рівень
- Розкласти на множники многочлени:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
7) Знайти корені рівняння ![]() .
.
IV рівень
-
Довести, що
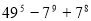 ділиться на 43.
ділиться на 43.
- Знайти найбільший корінь рівняння
![]() .
.
ІІ варіант
I рівень
1) Винести спільний множник за дужки: ![]() .
.
2) Розкласти ![]() на множники за формулою
на множники за формулою
![]() .
.
-
Розкласти
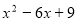 на множники за формулою
на множники за формулою
![]() .
.
II рівень
-
Розв'язати рівняння
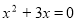 .
.
- Обчислити найзручнішим способом:
а)![]() ; б)
; б) ![]() .
.
III рівень
- Розкласти на множники многочлени:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
7) Знайти корені рівняння ![]() .
.
IV рівень
8) Довести, що ![]() ділиться на 29.
ділиться на 29.
9) Знайти найбільший корінь рівняння
![]() .
.
ІІІ варіант
I рівень
-
Винести спільний множник за дужки:
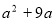 .
.
-
Розкласти
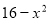 на множники за формулою
на множники за формулою
![]() .
.
-
Розкласти
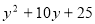 на множники за формулою
на множники за формулою
![]() .
.
II рівень
-
Розв'язати рівняння
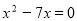 .
.
- Обчислити найзручнішим способом:
а)![]() ; б)
; б) ![]() .
.
III рівень
- Розкласти на множники многочлени:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
7) Знайти корені рівняння ![]() .
.
IV рівень
8) Довести, що ![]() ділиться на 41.
ділиться на 41.
9) Знайти найбільший корінь рівняння
![]() .
.
ІV варіант
I рівень
1) Винести спільний множник за дужки: ![]() .
.
2) Розкласти ![]() на множники за формулою
на множники за формулою
![]() .
.
-
Розкласти
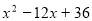 на множники за формулою
на множники за формулою
![]() .
.
II рівень
-
Розв'язати рівняння
 .
.
- Обчислити найзручнішим способом:
а)![]() ; б)
; б) ![]() .
.
III рівень
- Розкласти на множники многочлени:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
7) Знайти корені рівняння ![]() .
.
IV рівень
8) Довести, що ![]() ділиться на 11.
ділиться на 11.
9) Знайти найбільший корінь рівняння
![]() .
.
ТО № 6. “Застосування різних способів розкладання многочленів на множники”.
І варіант
І рівень
- Записати формулу суми кубів.
- Записати формулу різниці квадратів.
- Яка формула записана (а + b)2 = a2 + 2ab + b2?
ІІ рівень
- Розкласти на множники вирази:
а) а3 – 8; б) 4а2 – 9; в) х5 – 4х3; г) 27 + 8b3.
- Подати у вигляді многочлена:
( х + 4 ) · ( х2 – 4х + 16 ).
ІІІ рівень
- Розв’язати рівняння:
а) х3 – 36х = 0;
б) ( х – 2 ) · ( х2 + 2х + 4 ) = х3 + 2х.
IV рівень
- Довести, що 610 – 69 + 68 ділиться на 31.
- Розкласти на множники:
( n – 2 )2 – ( 3n + 1 )2.
ІІ варіант
І рівень
- Записати формулу різниці кубів.
- Записати формулу квадрат різниці двох виразів.
- Яка формула записана
а2 – b2 = ( a – b ) · ( a + b )?
ІІ рівень
- Розкласти на множники вирази:
а) b3 + 27; б) 16 – 25а2; в) х6 – 9х4; г) 64 – 8y3.
- Подати у вигляді многочлена:
( 2х – 1 ) · ( 4х2 + 2х + 1 ).
ІІІ рівень
- Розв’язати рівняння:
а) 64х – х3 = 0;
б) х3 – 7х2 – 4х + 28 = 0.
IV рівень
- Довести, що 2563 – 1493 ділиться на 107.
8. Розкласти на множники: 25 – ( 3х – 4 )2.
ІІІ варіант
І рівень
- Записати формулу суми кубів.
- Записати формулу різниці квадратів.
- Яка формула записана (а – b)2 = a2 – 2ab + b2?
ІІ рівень
- Розкласти на множники вирази:
а) b3 + 125; б) 100 – 16а2; в) 25х4 – х6; г) 8х3 – 27.
- Подати у вигляді многочлена:
( х – 4 ) · ( х2 + 4х + 16 ).
ІІІ рівень
- Розв’язати рівняння:
а) 100х – х3 = 0;
б) х3 + 4х2 – 9х – 36 = 0.
IV рівень
- Довести, що 1853 – 1783 ділиться на 7.
- Розкласти на множники: 81 – ( 5 – 2х )2 .
IV варіант
І рівень
- Записати формулу різниці квадратів.
- Записати формулу квадрат суми двох виразів.
- Яка формула записана
а3 – b3 = ( a – b ) · ( a2 + аb + b2 )?
ІІ рівень
- Розкласти на множники вирази:
а) b3 – 125; б) 36х2– 49; в) 9х3 – х5; г) 8 + 27а3.
- Подати у вигляді многочлена:
( 3 + 2х ) · ( 9 – 6х + 4х2 ).
ІІІ рівень
- Розв’язати рівняння: а) х3 – 49х = 0;
б) ( 4 + х ) · ( 16 – 4х + х2 ) = х3 + х .
IV рівень
- Довести, що 88 + 87 – 86 ділиться на 71.
- Розкласти на множники: ( х + 1 )2 – ( 2х – 3 )2.
ТО № 7. “Лінійне рівняння з двома змінними”.
І варіант
І рівень
- Що є розв’язком лінійного рівняння?
- Що означає, що точка належить прямій?
- Чи є пара чисел (1; 2) розв’язком рівняння
2х – 4у = – 6.
ІІ рівень
- Знайти розв’язок рівняння х + 3у = – 9.
- Замінити * числом, щоб пара (4; *) стала розв’язком рівняння 10х – 5у = 50.
ІІІ рівень
- Побудувати в системі координат графік рівняння х – 2у = – 8.
- Знайти коефіцієнт в рівнянні – 5х + bу = 15, щоб графік цього рівняння проходив через точку В(2; -5).
IV рівень
- Скласти рівняння, для якого пара (2; -3) є розв’язком.
- Серед розв’язків рівняння 6х – 4у = – 18 знайти таку пару чисел, щоб числа були однакові.
ІІ варіант
І рівень
- Яке рівняння називається лінійним?
- Що є графіком лінійного рівняння?
- Чи є пара чисел (1; 5) розв’язком рівняння 3х + 4у = 18.
ІІ рівень
- Знайти розв’язок рівняння 2х + 4у = 8.
- Замінити * числом, щоб пара (*; -3) стала розв’язком рівняння 4х + 2у = 18.
ІІІ рівень
- Побудувати в системі координат графік рівняння 2х + у = 6.
- Знайти коефіцієнт а рівняння ах + 3у = – 6 , щоб графік цього рівняння проходив через точку В(2; -2).
IV рівень
- Скласти рівняння, для якого пара (-4; 3) є розв’язком.
- Серед розв’язків рівняння 5х – у = 14 знайти таку пару чисел, щоб перше число було у три рази більше від другого.
ІІІ варіант
І рівень
- Що є розв’язком лінійного рівняння?
- Що означає, що точка належить прямій?
- Чи є пара чисел (4; -2) розв’язком рівняння 3х + у = 10.
ІІ рівень
- Знайти розв’язок рівняння 2х + 3у = – 9.
- Замінити * числом, щоб пара (-2; *) стала розв’язком рівняння
х – 5у = 8.
ІІІ рівень
- Побудувати в системі координат графік рівняння 2х – 3у = 9.
- Знайти коефіцієнт в рівнянні 5х – bу = 1, щоб графік цього рівняння проходив через точку В(-4; 3).
IV рівень
- Скласти рівняння, для якого пара (3; -1) є розв’язком.
- Серед розв’язків рівняння 2х – 3у = – 8 знайти таку пару чисел, щоб перше число було на 2 більше від другого.
IV варіант
І рівень
- Яке рівняння називається лінійним?
- Що є графіком лінійного рівняння?
- Чи є пара чисел (-3; 2) розв’язком рівняння 4х + у = – 1.
ІІ рівень
- Знайти розв’язок рівняння х – 5у = 15.
- Замінити * числом, щоб пара (*; -3) стала розв’язком рівняння – 2х + у = 7.
ІІІ рівень
- Побудувати в системі координат графік рівняння 2х + 3у = – 6.
- Знайти коефіцієнт а рівняння ах – 4у = 4 , щоб графік цього рівняння проходив через точку В(-3; 2).
IV рівень
- Скласти рівняння, для якого пара (-1; 6) є розв’язком.
- Серед розв’язків рівняння 6х – 3у = – 18 знайти таку пару чисел, щоб друге число було у чотири рази більше від першого.
ТО № 8. “Системи лінійних рівнянь”.
І варіант
І рівень
- Чи є пара чисел (1; 1) розв’язком системи
![]() х – у = –1
х – у = –1
2х + у = 4 .
-
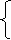 Визначити х: 7х = 10 + 4у
Визначити х: 7х = 10 + 4у
у = 1 .
ІІ рівень
- Розв’язати систему рівнянь способом підстановки
![]() х – у = 2
х – у = 2
3х – 2у = 9 .
- Розв’язати систему рівнянь способом додавання
![]() 5х – 2у = 6
5х – 2у = 6
– 7х – 2у = – 6 .
ІІІ рівень
- Швидкість катера за течією 36 км/год, а швидкість проти течії 28 км/год. Яка власна швидкість катера і швидкість течії?
IV рівень
- Знайти розв’язки системи:
![]() – 2 · (2х + 1) + 1,5 = 3 · (у – 2) – 6х
– 2 · (2х + 1) + 1,5 = 3 · (у – 2) – 6х
11,5 – 4 · (3 – х) = 2у – (5 – х) .
ІІ варіант
І рівень
- Чи є пара чисел (2; –1) розв’язком системи
![]() х + у = 1
х + у = 1
х – 2у = 3 .
-
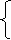 Визначити у: х = 2
Визначити у: х = 2
3у = 5 – х .
ІІ рівень
-
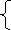 Розв’язати систему рівнянь способом підстановки
Розв’язати систему рівнянь способом підстановки
х – 2у = 11
–2х + у = –4 .
- Розв’язати систему рівнянь способом додавання
![]() 3х + у = 2
3х + у = 2
х + 2у = – 6 .
ІІІ рівень
- Один учень купив 5 олівців та 3 зошити, заплативши за це 70 коп. Другий учень купив за тими ж цінами 8 олівців та 3 зошити заплативши за все 94 коп. Скільки коштує олівець і зошит?
IV рівень
- Знайти розв’язки системи:
![]() 2 · (5х – 7) – 3 · (5 – 4у) = – 7
2 · (5х – 7) – 3 · (5 – 4у) = – 7
6 · (7у – 2) – (5 – 3х) = 23 .
ІІІ варіант
І рівень
- Чи є пара чисел (3; 6) розв’язком системи
![]() у – 2х = 0
у – 2х = 0
х – у = –3 .
-
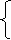 Визначити х: 5х = 2у – 1
Визначити х: 5х = 2у – 1
у = 3 .
ІІ рівень
-
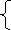 Розв’язати систему рівнянь способом підстановки
Розв’язати систему рівнянь способом підстановки
х + у = 6
2х + 2у = 1 .
- Розв’язати систему рівнянь способом додавання
![]() х – 2у = 2
х – 2у = 2
3х – 2у = – 2 .
ІІІ рівень
- Ательє першого разу пошило 3 костюми і 4 пальта, на які ви-
тратило 19 м сукна. Другого разу пошили 3 костюми і 6 пальт, на які витратили 24 м сукна. Скільки сукна потрібно на один костюм і одне пальто?
IV рівень
- Знайти розв’язки системи:
![]() 3 · (4х – 5) – 4 · (7 – 3у) = – 19
3 · (4х – 5) – 4 · (7 – 3у) = – 19
5 · (6у – 4) – (5 + 7х) = – 2 .
IV варіант
І рівень
- Чи є пара чисел (3; 1) розв’язком системи
![]() х + 2у = 5
х + 2у = 5
2х – у = 5 .
-
 Визначити у: х = 5
Визначити у: х = 5
2у = 3х – 3 .
ІІ рівень
-
 Розв’язати систему рівнянь способом підстановки
Розв’язати систему рівнянь способом підстановки
х + 5у = 7
3х – 2у = 4 .
- Розв’язати систему рівнянь способом додавання
![]() х – у = 2
х – у = 2
3х – 2у = 9 .
ІІІ рівень
- На пошиття 45 костюмів і 40 пальт витрачено 235 м сукна. На кожний костюм витрачали на 0,5 м більше сукна, ніж на пальто. Скільки сукна йшло на один костюм і одне пальто?
IV рівень
- Знайти розв’язки системи:
![]() 84 + 3 · (х – 3у) = 36х – 4 · (у + 17)
84 + 3 · (х – 3у) = 36х – 4 · (у + 17)
10 · (х – 4) = 3у + 4 · (1 – х) .
Підсумкова контрольна робота
І варіант
І рівень
1) Спростити вирази:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
ІІ рівень
2) Розв'язати рівняння ![]() .
.
3) Розв'язати систему рівнянь
![]()
![]()
ІІІ рівень
4) Розв'язати задачу за допомогою рівняння.
Велосипедист їхав 2 години лісом і 3 години по дорозі, проїхавши всього 42 км Швидкість велосипедиста по дорозі на 4 км/год більша ніж лісом. 3 якою швидкістю велосипедист їхав лісом, і з якою по дорозі?
IІ рівень
5) Розкласти на множники ![]() .
.
6) Довести, що вираз при всіх значеннях змінних дорівнює нулю
![]() .
.
II варіант
І рівень
1) Спростити вирази:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
ІІ рівень
2) Розв'язати рівняння ![]() .
.
3) Розв'язати систему рівнянь
![]()
![]()
ІІІ рівень
4) Розв'язати задачу за допомогою рівняння.
5) За 5 годин їзди поїздом і 2 години машиною турист проїхав 620 км. Яка швидкість поїзда і яка швидкість машини, якщо швидкість поїзда на 40 км/год більша ніж швидкість машини?
ІV рівень
6) Розкласти на множники ![]() .
.
7) Довести, що вираз при всіх значеннях змінних дорівнює нулю
![]() .
.
7 клас (геометрія)
ТО №1. “Основні геометричні фігури і їх властивості”
І варіант
І рівень
- Що таке півпряма?
- Сформулюйте основну властивість належності точок і прямих.
- Що таке трикутник?
ІІ рівень
![]() 4. АС = 5 см, СВ = 12 см.
4. АС = 5 см, СВ = 12 см.
А С В Знайти АВ.
5.
![]()
![]() М К
М К ![]() KMN = 68,
KMN = 68,
![]() DMN = 24.
DMN = 24.
Знайти ![]() KMD.
KMD.
N D
![]()
 6. В Т
6. В Т ![]() А = 75,
А = 75,

![]()
![]() В = 38,
В = 38,
![]() С = 67.
С = 67.
![]()
![]() S Н
S Н
А С
Знайти кути трикутника STH.
ІІІ рівень
7. Дано: ![]() (ab) = 80,
(ab) = 80, ![]() (ad) = 40,
(ad) = 40, ![]() (db) = 60.
(db) = 60.
Чи проходить промінь d між сторонами a і b?
8. Дано: MD = 24 см, точка N належить відрізку MD, MN у три рази більший ND. Знайти MN і ND.
ІV рівень
9. Скільки відрізків утворюють п’ять точок, що лежать на одній прямій?
![]() 10. А В K D
10. А В K D
K – середина відрізка BD, AD = 30 см, АВ = 6 см. Знайти довжину відрізка АК.
ІІ варіант
І рівень
- Що таке відрізок?
- Сформулюйте основну властивість розміщення точок на прямій.
- Які трикутники називаються рівними?
ІІ рівень
![]() 4. КР = 18 см, МР = 6 см.
4. КР = 18 см, МР = 6 см.
К М Р Знайти КМ.
5.
![]()
![]()
![]() В А
В А ![]() ABD = 35,
ABD = 35,
![]() DBC = 28 .
DBC = 28 .
С D Знайти ![]() АВC
АВC
![]()
![]() 6. Р АВ = 8 см,
6. Р АВ = 8 см,
![]()
![]() В ВМ = 5 см,
В ВМ = 5 см,
![]() С N АМ = 12 см.
С N АМ = 12 см.
![]() А М
А М
Знайти сторони трикутника CPN.
ІІІ рівень
7. Дано: RP = 8 см, RS = 12 см, PS = 4 см.
Чи розділяє точка Р точки R і S?
8. Дано: ![]() (kn) = 140, промінь а проходить між сторонами k і n,
(kn) = 140, промінь а проходить між сторонами k і n, ![]() (ka) на 60 менший від
(ka) на 60 менший від ![]() (an). Знайти
(an). Знайти ![]() (ka) і
(ka) і ![]() (an).
(an).
ІV рівень
9. Скільки кутів утворюють чотири промені, що виходять з однієї точки?
![]() 10. А С В D
10. А С В D
С – середина відрізка АB, AD = 34 см, ВD = 18 см. Знайти довжину відрізка CD.
ІІІ варіант
І рівень
- Що таке кут?
- Сформулюйте основну властивість вимірювання відрізків.
- Які прямі називаються паралельними?
ІІ рівень
4. АD = 14 см, DP = 8 см.
![]() А D P Знайти АP.
А D P Знайти АP.
5.

![]() T N
T N ![]() TMN = 94,
TMN = 94,
![]() TMH = 144.
TMH = 144.
Знайти ![]() NMH.
NMH.
![]() M H
M H

![]()

![]() 6. Z P
6. Z P ![]() S = 40,
S = 40,
![]() Y = 80,
Y = 80,
![]() Z = 60.
Z = 60.
![]()
![]() A X
A X
S Y
Знайти кути трикутника APX.
ІІІ рівень
7. Дано: ![]() (bm) = 130,
(bm) = 130, ![]() (bc) = 80,
(bc) = 80, ![]() (cm) = 50.
(cm) = 50.
Чи проходить промінь c між сторонами b і m?
8. Дано: KS = 26 см, точка A належить відрізку KS, KA на 6 см менший від AS. Знайти KA і AS.
ІV рівень
9. Скільки відрізків утворюють чотири точки, що лежать на одній прямій?
![]() 10. А В Р D
10. А В Р D
Р – середина відрізка BD, AD = 42 см, АВ = 10 см. Знайти довжину відрізка АР.
ІV варіант
І рівень
- Які півпрямі називаються доповняльними?
- Сформулюйте основну властивість вимірювання кутів.
- Які відрізки називаються рівними?
ІІ рівень
4. AM = 22 см, NМ = 16 см.
![]() А N М Знайти AN.
А N М Знайти AN.
![]() 5. P
5. P
 B
B ![]() PSB = 62,
PSB = 62,
![]() BST = 18.
BST = 18.
![]() S T Знайти
S T Знайти ![]() PST.
PST.
![]()
![]() C
C
![]()
![]() 6. L KL = 14 см,
6. L KL = 14 см,
![]() LA = 10 см,
LA = 10 см,
![]() B D KА = 18 см.
B D KА = 18 см.
K А
Знайти сторони трикутника BCD.
ІІІ рівень
7. Дано: BP = 18 см, BS = 30 см, PS = 20 см.
Чи належить точка Р точки BS?
8. Дано: ![]() CDP = 80, промінь DO проходить між сторонами
CDP = 80, промінь DO проходить між сторонами ![]() CDP,
CDP, ![]() CDO на 24 більший від
CDO на 24 більший від ![]() ODP. Знайти
ODP. Знайти ![]() CDO і
CDO і ![]() ODP.
ODP.
ІV рівень
9. Скільки кутів утворюють п’ять променів, що виходять з однієї точки?
![]() 10. K С В M
10. K С В M
С – середина відрізка KB, KM = 48 см, ВM = 26 см. Знайти довжину відрізка CM.
ТО № 2. “Суміжні і вертикальні кути”.
І варіант
І рівень
- Які кути називають суміжними?
- Яку властивість мають вертикальні кути?
- Що називається бісектрисою кута?
ІІ рівень
![]() 4. B
4. B ![]() АСВ = 54
АСВ = 54
Знайти ![]() BCD?
BCD?
А С D
![]()

 5.
5.
1 ![]() 1 = 137.
1 = 137.
-
4 Знайти
 3,
3,  2?
2?
2
ІІІ рівень
6. Сума двох кутів, утворених при перетині двох прямих, дорівнює 112. Знайти всі утворені кути.
7. Один із суміжних кутів на 62 менший від другого. Знайти суміжні кути.
 IV рівень
IV рівень
8. С ОВ – бісектриса
 В
В ![]() COD.
COD.
Знайти ![]() АОС,
АОС,
![]() якщо
якщо ![]() BOD = 20.
BOD = 20.
А О D
ІІ варіант
І рівень
- Які кути називають вертикальними?
- Яку властивість мають суміжні кути?
- Які прямі називаються перпендикулярними?
ІІ рівень
![]() 4. М
4. М ![]() MPN = 138
MPN = 138
Знайти ![]() DPM?
DPM?
D P N
![]()
 5.
5.
 1
1 ![]() 3 = 62.
3 = 62.
3 4 Знайти ![]() 1,
1, ![]() 4?
4?
2
ІІІ рівень
6. Сума двох кутів, утворених при перетині двох прямих, дорівнює 244. Знайти всі утворені кути.
7. Один із суміжних кутів у 4 рази більший від другого. Знайти суміжні кути.
IV рівень
![]() 8. D ОВ – бісектриса
8. D ОВ – бісектриса
 K
K ![]() COD.
COD.
Знайти ![]() АОС,
АОС,
якщо ![]() BOD = 20.
BOD = 20.
![]() А B C
А B C
ТО №3. “Ознака рівності трикутників. Рівнобедрений трикутник”.
І варіант
І рівень
- Сформулювати ІІ ознаку рівності трикутників.
- Бісектриса трикутника – це ...
![]()
![]() 3. N За якою ознакою
3. N За якою ознакою
![]() ∆MNP = ∆MKP?
∆MNP = ∆MKP?
![]()
![]()
![]() P M
P M
K
ІІ рівень
4. Відрізки KP і ST перетинаються в точці О. Відомо, що ![]() К =
К = ![]() Р, КО = ОР. Довести, що ∆КТО = ∆SOP.
Р, КО = ОР. Довести, що ∆КТО = ∆SOP.
5. Бічна сторона рівнобедреного трикутника 8 см, а периметр – 30 см. Знайти основу трикутника.
ІІІ рівень
6. Периметр рівнобедреного трикутника 29,2 см. Його бічна сторона на 5 см більша за основу. Знайти сторони трикутника.
IV рівень
![]()
![]()

 7. С В Дано: АО = ОD.
7. С В Дано: АО = ОD.
Що ще потрібно
О знати, щоб довести,
що СА = BD.
А D
8. Трикутник АВС рівнобедрений з основою АС, BD – бісектриса, точка К лежить на BD. Довести, що ![]() ВАК =
ВАК = ![]() ВСК.
ВСК.
ІІ варіант
І рівень
- Сформулювати І ознаку рівності трикутників.
- Висота трикутника – це ...
![]()
![]() 3. В За якою ознакою
3. В За якою ознакою
![]() ∆АВС = ∆ADC?
∆АВС = ∆ADC?
![]()
![]()
![]() А С
А С
D
ІІ рівень
4. Відрізки AB і CD перетинаються в точці О. Відомо, що AO = OD, CО = ОB. Довести, що ∆AOC = ∆DOB.
5. Основа рівнобедреного трикутника 5,2 см, а бічна сторона – 6,4 см. Знайти периметр трикутника.
ІІІ рівень
6. Периметр рівнобедреного трикутника 19,6 см. Його основа на 4 см більша за бічну сторону. Знайти сторони трикутника.
IV рівень
![]()


![]() 7. В D Дано: АВ = СD.
7. В D Дано: АВ = СD.
Що ще потрібно
знати, щоб довести,
що ![]() В =
В = ![]() D.
D.
![]() А C
А C
8. Трикутник АВС рівнобедрений з основою АС, BМ – медіана, точка D лежить на BМ. Довести, що AD = DC.
ІІІ варіант
І рівень
- Що таке медіана трикутника.
- Записати властивість медіани рівнобедреного трикутника.
![]()
![]() 3. Р За якою ознакою
3. Р За якою ознакою
![]() ∆КРМ = ∆KSM?
∆КРМ = ∆KSM?
![]()
![]()
![]() К M
К M
S
ІІ рівень
4. Відрізки DP і MN перетинаються в точці О. Відомо, що ![]() N =
N = ![]() M, NО = ОM. Довести, що ∆DON = ∆MOP.
M, NО = ОM. Довести, що ∆DON = ∆MOP.
5. Основа рівнобедреного трикутника 8 см, а периметр – 32 см. Знайти бічну сторону трикутника.
ІІІ рівень
6. Периметр рівнобедреного трикутника 24,9 см. Його бічна сторона на 6 см менша за основу. Знайти сторони трикутника.
IV рівень



 7. А С Дано:
7. А С Дано: ![]() А =
А = ![]() С.
С.
Що ще потрібно
знати, щоб довести,
В О D що АВ = СD.
8. Трикутник АВС рівнобедрений з основою АС, BD – бісектриса, точка Р лежить на BD. Довести, що АР = РС.
ІV варіант
І рівень
- Сформулювати ІІІ ознаку рівності трикутників.
- Рівнобедреним трикутником називається ...
![]()
![]()
![]() 3. В За якою ознакою
3. В За якою ознакою
∆АВD = ∆CBD?
![]()
![]() А С
А С
D
ІІ рівень
4. Відрізки AD і MC перетинаються в точці О. Відомо, що MO = OC, AО = ОD. Довести, що ∆AOM = ∆COD.
5. Бічна сторона рівнобедреного трикутника 7,5 см, а основа – 3,6 см. Знайти периметр трикутника.
ІІІ рівень
6. Периметр рівнобедреного трикутника 18,9 см. Його основа на 3 см менша за бічну сторону. Знайти сторони трикутника.
IV рівень

![]()
![]() 7. В С Дано: ВD = AС.
7. В С Дано: ВD = AС.
Що ще потрібно
знати, щоб довести,
що AВ = CD.
![]() А D
А D
8. Трикутник АВС рівнобедрений з основою АС, BК – висота, точка М лежить на BК. Довести, що ![]() AМК =
AМК = ![]() СМК.
СМК.
ТО №4. “Паралельність прямих.
Сума кутів трикутника”.
І варіант
І рівень
- Які кути називаються внутрішньо-односторонніми?
2. Чому дорівнює сума кутів трикутника?
3. Яку властивість мають внутрішні різносторонні кути?
II рівень
4.Один з кутів, утворених при перетині двох паралельних прямих січною, дорівнює 84°. Знайти решта утворені кути.
5. Кут при основі рівнобедреного трикутника дорівнює 54°. Знайти кут при вершині трикутника.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 238°. Знайти всі утворені кути.
7. Кут при основі рівнобедреного трикутника на 36° більший від кута при вершині. Знайти кути трикутника.
IV рівень
8. У трикутнику КNМ ![]() К = 90°, а
К = 90°, а ![]() N = 62°. На продовженні катета КМ відкладений відрізок КS, що дорівнює КN. Знайти кути трикутника MSN.
N = 62°. На продовженні катета КМ відкладений відрізок КS, що дорівнює КN. Знайти кути трикутника MSN.
ІІ варіант
І рівень
- Які кути називаються різносторонніми?
2. Який трикутник називається прямокутним?
3. Яку властивість мають внутрішні односторонні кути?
II рівень
4. Один з кутів, утворених при перетині двох паралельних прямих січною, дорівнює 136°. Знайти решта утворені кути.
5. Кут при вершині рівнобедреного трикутника дорівнює 86°. Знайти кут при основі трикутника.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 152°. Знайти всі утворені кути.
7. Кут при вершині рівнобедреного трикутника на 72° менший від кута при основі. Знайти кути трикутника.
IV рівень
8. У трикутнику АВС ![]() А = 90°, а
А = 90°, а ![]() С = 78°. На продовженні гіпотенузи ВС відкладений відрізок CD, що дорівнює АС. Знайти кути трикутника ABD.
С = 78°. На продовженні гіпотенузи ВС відкладений відрізок CD, що дорівнює АС. Знайти кути трикутника ABD.
ІІІ варіант
І рівень
- Які кути називаються внутрішньо-односторонніми?
2. Чому дорівнює сума гострих кутів прямокутного трикутника?
3. Який кут називається зовнішнім кутом трикутника?
II рівень
4.Один з кутів, утворених при перетині двох паралельних прямих січною, дорівнює 78°. Знайти решта утворені кути.
5. Кут при основі рівнобедреного трикутника дорівнює 65°. Знайти кут при вершині трикутника.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 266°. Знайти всі утворені кути.
7. Кут при основі рівнобедреного трикутника на 30° менший від кута при вершині. Знайти кути трикутника.
IV рівень
8. У трикутнику APD ![]() A = 90°, а
A = 90°, а ![]() D = 56°. На продовженні катета AD відкладений відрізок AB, що дорівнює AP. Знайти кути трикутника BPD.
D = 56°. На продовженні катета AD відкладений відрізок AB, що дорівнює AP. Знайти кути трикутника BPD.
ІV варіант
І рівень
- Які кути називаються внутрішніми різносторонніми?
2. Чому дорівнює сума кутів трикутника?
3. Як називаються сторони прямокутного трикутника?
II рівень
4. Один з кутів, утворених при перетині двох паралельних прямих січною, дорівнює 145°. Знайти решта утворені кути.
5. Кут при вершині рівнобедреного трикутника дорівнює 74°. Знайти кут при основі трикутника.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 138°. Знайти всі утворені кути.
7. Кут при вершині рівнобедреного трикутника на 27° більший від кута при основі. Знайти кути трикутника.
IV рівень
8. У трикутнику BMN ![]() B = 90°, а
B = 90°, а ![]() N = 54°. На продовженні гіпотенузи MN відкладений відрізок MA, що дорівнює BM. Знайти кути трикутника ABN.
N = 54°. На продовженні гіпотенузи MN відкладений відрізок MA, що дорівнює BM. Знайти кути трикутника ABN.
ТО № 5. “Геометричні побудови”.
І варіант
І рівень
- Що таке коло?
- Де лежить центр кола, вписаного в трикутник?
- Намалювати коло, провести радіус.
ІІ рівень
- Накреслити довільний відрізок і знайти його середину.
- Накреслити довільний гострокутний трикутник і побудувати одну з його бісектрис.
ІІІ рівень
-

 АС – дотична, відрізок АВ –
АС – дотична, відрізок АВ –
хорда кола з центром в точці О,
О ВАС = 76°.
 А В Знайти величину АОВ.
А В Знайти величину АОВ.
С
IV рівень
- Побудувати трикутник за двома сторонами і кутом між ними.
ІІ варіант
І рівень
- Яке коло називається описаним навколо трикутника?
- Де лежить центр кола, описаного навколо трикутника?
- Намалювати коло, провести дотичну до нього.
ІІ рівень
- Накреслити довільний кут і побудувати його бісектрису.
- Накреслити довільний тупокутний трикутник і побудувати одну з його медіан.
ІІІ рівень

![]()
 А О Пряма АС – дотична, АВ – хорда кола з
А О Пряма АС – дотична, АВ – хорда кола з
центром в точці О, АОВ = 70°. Знайти
В ВАС.
С
IV рівень
- Побудувати рівнобедрений трикутник за бічною стороною і висотою, проведеною до основи.
ІІІ варіант
І рівень
- Що таке дотична?
- Де лежить центр кола, вписаного в трикутник?
- Намалювати коло, провести діаметр.
ІІ рівень
- Накреслити довільну пряму а і позначити на ній точку А. Провести через точку А пряму, перпендикулярну до прямої а.
- Накреслити довільний трикутник і побудувати одну з його бісектрис.
ІІІ рівень
-

 АС – дотична, відрізок АВ –
АС – дотична, відрізок АВ –
хорда кола з центром в точці О,
О ВАС = 66°.
 В Знайти величину АОВ.
В Знайти величину АОВ.
А
С
IV рівень
- Побудувати трикутник за стороною і двома прилеглими до неї кутами.
IV варіант
І рівень
- Яке коло називається вписаним в трикутник?
- Де лежить центр кола, описаного навколо трикутника?
- Намалювати коло, провести хорду.
ІІ рівень
- Накреслити довільний тупий кут і поділити його пополам.
- Накреслити довільний трикутник і побудувати одну з його медіан.
ІІІ рівень
-
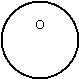 АС – дотична, відрізок АВ –
АС – дотична, відрізок АВ –

![]() хорда кола з центром в точці О, АОВ = 126°. Знайти ВАС.
хорда кола з центром в точці О, АОВ = 126°. Знайти ВАС.
А В
С
IV рівень
- Побудувати рівнобедрений трикутник за основою і медіаною, проведеною до основи.
Підсумкова контрольна робота
І варіант
І рівень
1. Визначити вид кута, якщо його градусна міра 68°.
2. Накреслити коло. Провести в ньому хорду.
3. Чи можуть два суміжні кути дорівнювати 83° і 107°?
II рівень
4. Точка D лежить між точками К і F. Знайти КF, якщо КD = 2,7 см, DF = 11,6 см.
5. Один з кутів, утворених при перетині двох прямих, дорівнює 118°. Визначити решту кутів.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 126°. Визначити всі кут.
7. Периметр рівнобедреного трикутника 6,4 м. Його основа на 2 м менша за бічну сторону. Знайти сторони трикутника.
IV рівень
8. АК – бісектриса рівнобедреного трикутника АВС з основою АС. Знайти ![]() АКС, якщо
АКС, якщо ![]() В = 80°.
В = 80°.
II варіант
І рівень
1. Визначити вид кута, якщо його градусна міра 124°.
2. Накреслити коло. Провести в ньому діаметр.
3. Чи можуть два суміжні кути дорівнювати 76° і 104°?
II рівень
4. Точка М лежить між точками А і В. Знайти АМ, якщо
АВ = 18,8 см, МВ = 5,5 см.
5. Один з кутів, утворених при перетині двох прямих, дорівнює 27°. Визначити решту кутів.
III рівень
6. Сума двох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 284°. Визначити всі кути.
7. Периметр рівнобедреного трикутника 9,6 м. Бічна сторона на 3 м більша за основу. Знайти сторони трикутника.
IV рівень
8. АК – висота рівнобедреного трикутника АВС з основою АС. Знайти ![]() В, якщо
В, якщо ![]() САК = 20°.
САК = 20°.


про публікацію авторської розробки
Додати розробку
