Южненська загальноосвітня школа І-ІІІ ступенів

Підготувала і провела

вчитель математики

Мордюкова Тетяна Федорівна

Тема. Теореми синусів і косинусів.

Мета: навчити учнів розв’язувати задачі з використанням теорем синусів і косинусів та наслідків з них; розвивати здібності учнів та інтерес до математики через розв’язування нестандартних задач; формувати зацікавленість у результатах спільної роботи; виховувати почуття взаємодопомоги, взаємо підтримки.

Обладнання: картки, таблиці, підручник.

«Найкращий спосіб вивчити що-небудь –

це відкрити його самому»

Д.Пойа

ХІД УРОКУ

І. Мотивація навчальної діяльності.

ІІ. Робота у «Творчій лабораторії».

Біля дошки двоє учнів працюють за картками: «роблять відкриття», розв’язуючи задачі.

Задача 1. Доведіть, що бісектриса кута трикутника ділить протилежну сторону на відрізки, пропорційні до протилежних сторін. (Властивість бісектриси трикутника.)

Задача 2. Як знайти радіус кола, описаного навколо трикутника, знаючи його сторони? Складіть алгоритм розв’язування задачі.

ІІІ. Актуалізація опорних знань.

1. Математичний диктант.

    1. Якщо в трикутнику відомі дві сторони b і c та кут між ними, то третя сторона        дорівнює…

    2. Якщо в трикутнику відомі сторона a та два прилеглі до неї кути  і , то дві інші сторони можна знайти так …

    3. Якщо в трикутнику відомі дві сторони  b і c та проекція однієї з них на другу, то третя сторона дорівнює …

4. Сума квадратів діагоналей паралелограма дорівнює …

5. У трикутнику проти більшої сторони лежить …

6. У трикутнику проти меншого кута лежить …

7. Який кут трикутника найбільший, якщо його сторони a = 7, b = 9, c = 5?

8. Який вид має трикутник, якщо a : b : c = 9 : 6 : 10?

9. Трикутник зі сторонами 3 см, 4 см, 5 см …

( Учні, що сидять за однією партою, міняються зошитами та виконують взаємоперевірку. Правильні відповіді записані заздалегідь на закритій частині дошки.)

2. Мозковий штурм.

1. Сформулюйте та символічно запишіть теореми синусів і косинусів.

2. Сформулюйте наслідки з теорем синусів і косинусів.

3. Що означає «розв’язати трикутник»?

4. за опорними малюнками знайдіть x:

А).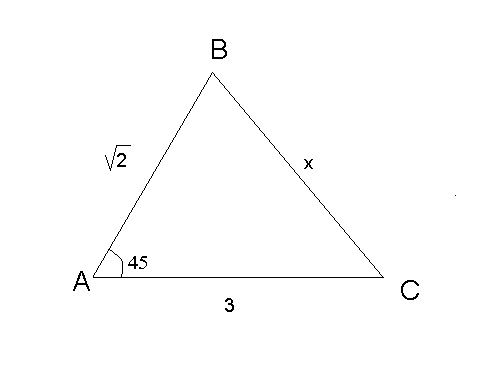                            

Б).

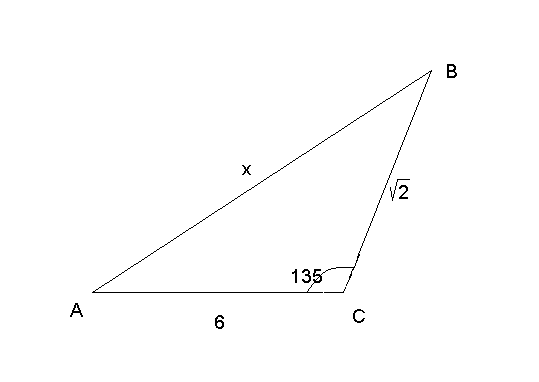
В).

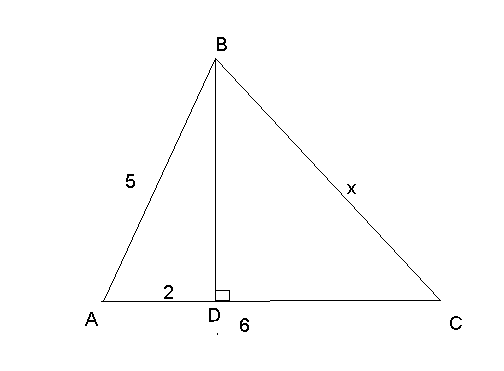
Г).

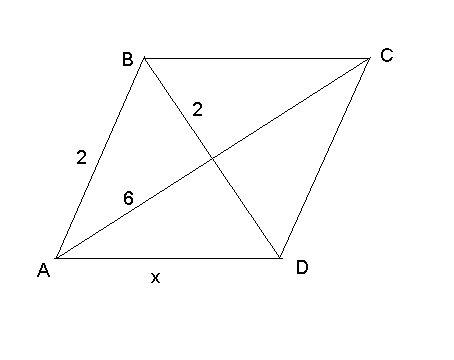
IV. Удосконалення знань, умінь і навичок.

Використовується метод проектів. Учні працюють у п’яти групах (одна група експертів, одна група консультантів і три групи практиків), розв’язують одну і ту саму задачу, яку можна розв’язати різними способами. Завдання – вибрати той спосіб розв’язування, який є раціональнішим, цікавішим, доступнішим, та обґрунтувати свій вибір.

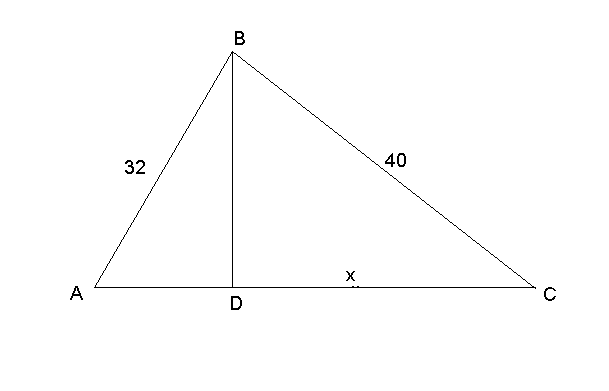
Задача. Відстань від транспортера до баржі 48 м. довжина першої стрічки транспортера 32 м, а другої, що подає зерно на баржу, 40 м. Знайдіть відстань від баржі до основи складського приміщення.

1. Група експертів під час захисту проектів рецензує роботу інших груп за планом:

   - спосіб розв’язування;

   - якість виконаної роботи;

   - якість оформлення малюнка;

   - математична мова (логічність, доказовість, використання термінології).

2. Група консультантів надає допомогу тим, хто її потребує.

3. Три групи практиків розв’язують задачу, а капітан презентує розв’язання задачі біля дошки.

V. Підведення підсумків.

1. Чого ви навчилися на уроці?

2. Що вам найбільше сподобалося?

3. Що корисного взяли від уроку?

VI. Домашнє завдання.

Повт п.109, п.110. № 26 (а), № 27 (а), № 28 (а).