Задачі практичного змісту в шкільному курсі математики

Задачі практичного змісту в шкільному курсі математики

1. Відсотки (формула складних відсотків)

1. Від тривалого  зберігання ячмінь втрачає за перший рік 3%  своєї маси, а за кожний наступний рік по 1%. Скільки ячменю залишиться у СФГ «Івашина» від 20 т ячменю через 3 роки  зберігання? Відповідь округлити до одиниць.

Розв'язання

20000  0,03 = 600 (кг) – втрати  ячменю за перший  рік.

20000 – 600 = 19400 (кг) – маса ячменю після першого року зберігання.

Використаємо формулу складних відсотків

А_n = А₀ (1 + )ⁿ, 

де p = 1%, n = 2,  А₀ = 19400 кг.

Оскільки ячмінь втрачає у масі, то у  формулі замість знака «+» буде знак «-».

А₂ = 19400 (1 - )² = 19400  0,99² =19400  0,9801 =  19013,94 кг

Отже,  через 3 роки зберігання від 2 т ячменю залишиться 19013,9419014 кг.

Відповідь: 19014 кг

2. Площі фігур. Практична задача

Учні  виступають  в ролі дизайнерів підлоги та паркетників, яким треба виконати таку роботу:

Задача. Виконати укладання паркетної підлоги в залі розміром 5,75  8 м. Паркет укласти  в ряди так, щоб паралелограми чергувалися з трапеціями, а трикутників у одному ряді було лише два.

Паркетні плитки мають форму прямокутного трикутника, паралелограма й рівнобічної трапеції з такими розмірами:

20

Скільки потрібно паркетних плиток кожного виду, щоб укласти підлогу в залі?

Розв'язання

Щоб виконати це завдання, треба знати, скільки і яких паркетних плиток знадобиться для покриття підлоги. 

Площа однієї смуги завширшки 20 см і довжиною 575 см буде 20575=11 500 см².

Площа прямокутного трикутника S= ,  S= (см²), тоді площа двох трикутників  дорівнюватиме 300 см².

Площа паралелограма  обчислюється за формулою S= ah, S=35  20 =700 (см²), а площа трапеції – за формулою S =   S = =700 (см²). Обчисливши  (11500-300): 700 = 16, бачимо, що в одній смузі по ширині ігрового залу поміститься по 8 паралелограмів і трапецій.  Таких смуг у довжині кімнати поміститься 800:20=40. Отже, для настилання підлоги знадобиться:

трикутників – 240=80;

паралелограмів - 840=320;

трапецій - 840=320.

 Перевіркою встановлюється:

 площа ігрового залу 575800 = 460 000 (см²);

 площа однієї смуги 57520 = 11 500 (см²);

таких смуг 40, тому 1150040 = 460 000 (см²) - площа паркетної  підлоги.

Висновок.

Вартість укладання будь-якого паркету (березового, дубового, бамбукового, керамічного,  коркового)  можна порахувати самостійно. Потрібно лише знати все необхідне: площу кімнати, площу однієї плитки,  кількість плиток, ціну за квадратний метр укладання в залежності від виду, типу і характеристик паркету.

Відповідь: трикутних плиток – 80 штук, паралелограмів  - 320 штук, трапецій – 320 штук.

3. Стандартний вигляд числа

На території Києво-Печерської лаври розташовано Музей мікромініатюри знаного у всьому світі майстра Миколи Сядристого. Тут експонується «Троянда у волосині»: всередині волосся по його довжині просвердлено порожнину і відполіровано до прозорості. Потім всередину вставлена гілочка троянди, товщиною 0,05 мм. Найменша в світі книга: «Кобзар» Шевченка площею 0,6 мм². У ній 12 сторінок з віршами та малюнками. Товщина букв в цій книзі 0,0035мм. Сторінки зшиті... павутинкою, обкладинка і листки - з пелюсток безсмертника. Фрегат, довжиною 3,5 мм, товщина оснастки 0.003 мм. Модель складається з 337 деталей.

Задача.  Записати товщину троянди,  товщину букв в «Кобзарі» та довжину фрегата у стандартному вигляді. Подати кожне з них в системі СІ.

Розв’язання

Товщина троянди – 0,05мм=510^-2мм=510^-3см=510^-5м

Товщина букв – 0,0035мм=3,5 10^-3мм=3,5 10^-4см=3,5 10^-6м

Довжина фрегата -3,5мм=3,5 10^-1см = 3,5 10^-3м

Відповідь: 510^-5м, 3,5 10^-6м,  3,5 10^-3м.

4. Елементи   комбінаторики

Задача. В Україні 17 аеропортів мають чинний сертифікат на виконання авіаційних перевезень. Кожні два з них мають авіасполучення. Скільки авіаліній  в Україні?

Розв’язання

Кожна авіалінія сполучає два  аеропорти. Першим можна взяти будь-який із 17 аеропортів (аеропорт А), а другим – будь-який із 16 (аеропорт Б), що залишилися. Помноживши ці числа, одержимо 17∙16 = 272. Однак при цьому кожну авіалінію врахували двічі (перший раз, коли першим було вибрано аеропорт А, а другим – аеропорт Б, другий раз -  коли навпаки)

272 : 2 = 136 =

===136 (авіаліній)

Відповідь: 136 авіаліній

5. Гармонійні коливання (10 клас з поглибленим вивченням математики)

При диханні наші легені увесь час роблять коливальні рухи (то розширюючись, то стискаючись). Об’єм повітря, яке потрапляє до легень, обчислюють за зміною обводу грудної клітки.

Задача. Побудувати графік дихання учня нашого класу, що веде здоровий спосіб життя та побудувати графік

Розв’язання

Виміряємо (у сантиметрах) обвід грудної клітки учня класу під час видиху (V₁)  і вдиху  (V₂).

Маємо:  V₁=89 см,  V₂=97 см

Зміну обводу клітки знаходимо так:   ΔV = V₂ - V₁ = 97 – 89 = 8(см)

Тоді амплітуда гармонійного коливання

А =

За 60 секунд (t) учень зробив 23 (n) вдихи. Знайдемо період коливань Т:

Т = = = 2,6

Обчислимо   частоту коливань:

ω = =

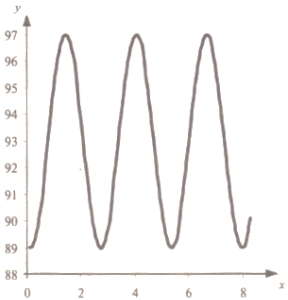
Складемо формулу гармонійного коливання:

y = 4Sin((х - )) + 93

Побудуємо відповідний графік.

6. Об’єми многогранників

В Японії розробили технологію вирощування кавунів, які мають кубічну форму, з метою знизити витрати на транспортування, оскільки товар кубічної форми займає менше місця і менше пошкоджується.

Український фермер Валерій Подольський  також запустив проєкт по вирощуванню кубічних кавунів. За смаковими якостями вони не відрізняються від звичайного кавуна.

Задача.  Оцініть масу  кавуна, що має форму куба,  якщо його ребро дорівнює 15см, а щільність кавуна близька до щільності води. На скільки збільшиться маса кавуна, якщо він підросте ще на 5 см?

Розв’язання

Знайдемо об’єм куба зі стороною 15 см.

 а = 15см = 0,15м,  V_куба= а³,   V₁ = 0,15³ = 0,003375м³. Маса кавуна 3кг 375г.

Якщо сторона кавуна  збільшиться на 5 см, тобто буде 20 см = 0,2 м, то 

V₂ = 0,2³ = 0,008м³ . Маса  кавуна – 8кг.

Отже, об’єм кавуна збільшиться  на V = V₂ – V₁,     V = 0,008 – 0, 003375 = 0,004625 м³

Об’єм та маса кавуна, якщо він стиглий, прямо пропорційні.  Тоді  якщо кавун підросте на 5 см, то його  маса збільшиться на 4 кг 625г

Відповідь; 4 кг  625г