Тести з алгебри 11 класу по темі "Похідна та її застосування"

Приклади  тестових завдань завдань з алгебри в 11 класі  на тему «Похідна та її застосування»

Варіант 1

1. Знайти похідну функції: у = 2х² + х.

        а) 4х² + 1.;    б) 2х + 1;     в) 2х ;     г) 4х + 1.

2.  Знайти похідну функції: у = 2 + cos х.

        а) 2 + sin x;    б) 2 – sin x;     в) –sin x ;     г) sin x.

3.  Обчислити значення похідної функції: у = х³ + 1 у точці х = 1.

        а) 2 ;    б) 1;     в) 3 ;     г) 4.

4. Обчислити значення похідної функції: у = sinx у точці х = π/4.

        а)  -;    б) ;     в) - ;     г) .

5. Дано  функцію у = х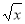. Її похідна дорівнює:

        а) ;    б) ;     в) ;     г) .

6. Розв’язати рівняння: у′ = 0, якщо у = х² - 4 х.

        а) -4;    б) -2;     в) 2 ;     г) 4.

7. Знайти критичну точку функції: у = 2х² - 4х.

        а) -1;    б) 1;     в) 0 ;     г) 2.

8. Знайти критичні точки функції: у = 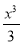+ х² - 3х +4.

        а) -1 і 3;    б) -3 і 1;     в) 1 і 3 ;     г) -1 і 2.

9. Розв’язати нерівність у′ ≥ 0, якщо у = 10х - х².

        а) ( - ∞; 5);    б) ( - ∞; 5];     в) ( 5; ∞) ;     г) ( - 5; ∞).

10.  Знайти проміжки спадання функції: у = х³ - 48х.

        а) ( - ∞; -4);    б) ( - 4; 4);     в) ( 4; ∞);     г) ( - ∞; ∞) .

11.  Критичними точками функції у = х – cos х є точки:

        а) + πn, n є Z;    б) 2πn, n є Z;       в) - + πn, n є Z;   г) πn, n є Z;

12. Знайти точки екстремуму функції: у = 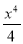- х³  + х² +1.

        а) -1; 0; 1.    б) 1; 0;      в) 0 ;1; 2;     г) 0; 2.

Варіант 2

1. Знайти похідну функції: у = .

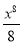        а) ;    б) ;     в) ;     г) х⁷.

2.  Знайти похідну функції: у = 1 + sin x.

        а)  sin x;    б) cos х;     в) – cos х;     г) 1.

3.  Обчислити значення похідної функції у = 6х² у точці х = 4.

        а) 30 ;    б) 45;     в) 50 ;     г) 48.

4. Обчислити значення похідної функції: у = sin x у точці х = π/3.

        а)  ;    б) ;     в) - ;     г).

5. Дано  функцію у = 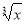. Її похідна дорівнює:

        а) ;    б);     в) ;     г)

6. Розв’язати рівняння: у′ = 0, якщо у = х² + 8 х.

        а) -4;    б) -2;     в) 2 ;     г) 5.

7. Знайти критичну точку функції: у = х² - 4.

        а) -4;    б) 4;     в) 0 ;     г) 2.

8. Знайти критичні точки функції: у = 3х⁴ – 16х³ + 18х² + 5.

        а) -1 і 3;    б) -3 і 1;     в) 1 і 3 ;     г) -1 і 2.

9. Розв’язати нерівність у′ ≥ 0, якщо у = 4х - х².

        а) ( - ∞; 2);    б) ( - ∞; 2];     в) ( 4; ∞) ;     г) ( - 4; ∞).

10.  Знайти проміжки спадання функції: у = х³ - 12х.

        а) ( - ∞; -2);    б) ( - 2; 2);     в) ( 2; ∞);     г) ( - ∞; ∞) .

11.  Критичними точками функції у = х + sin x є точки:

        а) + πn, n є Z;    б) π + 2πn, n є Z;       в) - + πn, n є Z;   г) πn, n є Z;

12.  Знайти точки екстремуму функції: у = 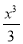- х²  - 8х +1.

        а) -2;  1.    б) 1; 2;      в) -2; 4;     г) 4; 2.