Тестові завдання на відповідність по темах алгебри 11 класу
ВІДДІЛ ОСВІТИ ПІДВОЛОЧИСЬКОЇ СЕЛИЩНОЇ РАДИ
НВК «ІВАНІВСЬКИЙ ЗНЗ І-ІІІ СТУПЕНІВ - ДНЗ»
Збірник
тестових завдань на відповідність
Алгебра 11 клас
Тернопіль
«Підручники &посібники»
2019
Матеріали підготувала Семенюк Любомира Адамівна (НВК «Іванівський ЗНЗ І-ІІІ ступенів -- ДНЗ»)
Рецензенти:
Білан Н.Я. – методист методичного кабінету відділу освіти Підволочиської селищної ради
Схвалено на засіданні науково-методичної ради Методичного кабінету відділу освіти Підволочиської селищної ради
Передмова
Проблема оцінювання знань школярів набула сьогодні особливої актуальності. Якість освіти безпосередньо пов’язують з системою оцінювання всіх складових навчально-виховного процесу – навчальних досягнень учнів, ефективністю роботи кожного вчителя і школи в цілому. Чим об’єктивнішим буде це оцінювання, тим якіснішою стане освіта. Визнаним у світі інструментами педагогічного оцінювання та вимірювання є тестові технології, які все частіше використовуються в школі. Потужним стимулом і викликом стало обов’язкове зовнішнє незалежне оцінювання (ЗНО) випускників шкіл.
Даний збірник призначений для тестової перевірки засвоєння учнями основного рівня курсу алгебри 11 класу.
Завдання збірника розподілено на вісім розділів по чотири варіанти у кожному:
- показникова функція, показникові рівняння та нерівності;
- логарифмічна функція, логарифмічні рівняння та нерівності;
- елементи комбінаторики,
- елементи теорії ймовірностей та математичної статистики;
- похідна функції;
- геометричний та фізичний зміст похідної;
- застосування похідної до дослідження функції;
- визначений інтеграл. Формула Ньютона-Лейбніца.
Тестові завдання дозволяють за короткий час перевірити об’єм вивченого матеріалу, швидко діагностувати оволодіння учнями основного рівня підготовки з окремих навчальних тем.
Дані тести можна використовувати як для індивідуальної перевірки, так і окремими завданнями на самостійних чи контрольних роботах.
Показникова функція, рівняння та нерівності
Варіант 1
- Встановити відповідність між заданими нерівностями та значенням а.
|
А 1 |
|
Б 3,7 |
|
В 0,4 |
|
|
Г -2 |
- Встановити відповідність між заданими рівняннями та їх коренями.
|
А -3 |
|
Б -1 |
|
В 3 |
|
Г -2 |
|
|
Д 1 |
- Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
|
А [ -2; ∞) |
|
Б ( +2; ∞) |
|
В ( - ∞; 2) |
|
Г [ 0; ∞) |
|
|
Д [ -4; ∞) |
Варіант 2
- Встановити відповідність між заданими нерівностями та значенням а.
- а-6 < а-2 А -1
- а0,15 > а0,36 Б 2,5
- а5 = а-4 В 0,3
Г 1
- Встановити відповідність між заданими рівняннями та їх коренями.
-
3х =
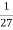 А 2
А 2
-
(
 )х = 9 Б -3
)х = 9 Б -3
- 9х = 81 В 3
-
(
 )х = 9 Г -1
)х = 9 Г -1
Д -2
- Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
- 0,5х ≥ 2 А [ -2; ∞)
-
6х ≥
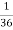 Б ( - ∞; -1)
Б ( - ∞; -1)
-
4х <
 В ( - ∞; -1]
В ( - ∞; -1]
- 8х ≤ 1 Г [ -1; ∞)
Д [ - ∞; 0)
Варіант 3
1. Встановити відповідність між заданими нерівностями та значенням а.
|
А 0,5 |
|
Б 5,1 |
|
В 1 |
|
|
Г -2,3 |
2. Встановити відповідність між заданими рівняннями та їх коренями.
|
А -3 |
|
Б -4 |
|
В |
|
Г -2 |
|
|
Д |
3. Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
|
А [ -3; ∞) |
|
Б ( 2; ∞) |
|
В ( - ∞; 1) |
|
Г [ 0; ∞) |
|
|
Д ( -∞; 0] |
Варіант 4
1. Встановити відповідність між заданими нерівностями та значенням а.
- а-8,7 < а-7,8 А 1
- а0,8 > а0,78 Б 4,8
- а8 = а-8 В -4,3
Г 1
2. Встановити відповідність між заданими рівняннями та їх коренями.
-
4х =
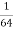 А 2
А 2
-
(
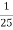 )х = 5 Б -3
)х = 5 Б -3
-
49х = 7 В

-
(0,5)х = 4 Г -
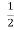
Д -2
3. Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
-
 х ≥
х ≥ 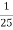 А ( 4; ∞)
А ( 4; ∞)
-
3х >
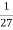 Б ( - 3; ∞)
Б ( - 3; ∞)
- 2х ≤ 16 В ( - ∞; 2]
-
(
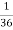 )х > 6 Г [ -
)х > 6 Г [ -  ; ∞)
; ∞)
Д ( - ∞; 4)
Логарифмічна функція, рівняння та нерівності
Варіант 1
- Встановити відповідність між виразами та їх значеннями
-
log27 3 А -

- log81 1 Б 3
- log1/3 27 В 0
- log3 27 Г -3
Д ![]()
- Встановити відповідність між заданими рівняннями та їх коренями.
- log5 х = 2 А 5
- log5 (-х) = 1 Б -5
- log1/5 х = -1 В 25
-
log25 х = -
 Г
Г 
Д - ![]()
- Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
- log3 х < 0 А ( 1; ∞)
- log3 (-х) < 0 Б ( - ∞; -1)
- log3 х > 0 В ( - ∞; 1)
- log3 (-х) > 0 Г ( -1; 0)
Д ( 0; 1)
Варіант 2
- Встановити відповідність між виразами та їх значеннями
- log25 5 А 3
- log5 125 Б -1
- log1/5 1 В 0
- log1/25 25 Г -3
Д ![]()
- Встановити відповідність між заданими рівняннями та їх коренями.
- log3 х = -4 А - 81
- log3 (-х) = 4 Б - 64
-
log4 х = -3 В
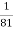
-
log4 (-x) = 3 Г
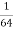
Д - ![]()
- Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
- log0,4 х < 0 А ( 1; ∞)
- log0,4 (-х) < 0 Б ( - ∞; -1)
- log0,4 х > 0 В ( - ∞; 1)
- log0,4 (-х) > 0 Г ( -1; 0)
Д ( 0; 1)
Варіант 3
1. Встановити відповідність між виразами та їх значеннями
- log4 16 А - 2
- log16 4 Б 2
- log2 16 В 0
- log16 1 Г 4
Д ![]()
2. Встановити відповідність між заданими рівняннями та їх коренями.
- log6 х = 36 А -36
-
log36(-х) =
 Б 2
Б 2
- log1/6 х = -2 В - 6
- log1/36 (-х) = - 1 Г 6
Д 36
3. Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
- log0.7 х ≥ 0 А [ 1; ∞)
- log0.7 (-х) ≥ 0 Б ( - ∞; -1]
- log0.7 x ≤ 0 В ( - ∞; 1]
- log0.7 (-х) ≤ 0 Г [ -1; 0)
Д ( 0; 1]
Варіант 4
1. Встановити відповідність між виразами та їх значеннями
- log7 49 А 2
-
log49 7 Б -

- log49 1 В 0
- log1/7 49 Г -2
Д ![]()
2. Встановити відповідність між заданими рівняннями та їх коренями.
- log1/4 х = -2 А - 2
-
log1/16 х =
 Б - 16
Б - 16
-
log16 х =
 В 16
В 16
-
log4 (-x) = 2 Г

Д 2
3. Встановити відповідність між заданими нерівностями та множинами їх розв’язків.
- log5 х ≥ 0 А [ 1; ∞)
- log5 (-х) ≤ 0 Б ( - ∞; -1]
- log5 х ≤ 0 В ( - ∞; 1)
- log5 (-х) ≥ 0 Г [ -1; 0)
Д ( 0; 1]
Елементи комбінаторики.
Варіант 1
- Встановити відповідність між виразами та їх значеннями
-
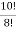 А 40
А 40
-
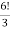 Б 90
Б 90
- 2! + 4! В 80
- 4*4! - 42 Г 240
Д 36
- Встановити відповідність між заданими позначеннями кількостей сполук та їх числовими значеннями
- С93 А 11
- С710 Б 45
- С1012 : Р3 В 84
- А210 – С210 Г 120
Д 60
Варіант 2
1. Встановити відповідність між виразами та їх значеннями
-
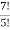 А 180
А 180
-
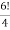 Б 42
Б 42
- 3! + 5! В 115
- 5! - 5 Г 126
Д 96
2. Встановити відповідність між заданими позначеннями кількостей сполук та їх числовими значеннями
- С82 А 28
- А37 Б 100
- С912 - Р5 В 210
- А310 : С310 Г 12
Д 6
Варіант 3
1. Встановити відповідність між виразами та їх значеннями
-
 А 30
А 30
-
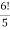 Б 9
Б 9
- 3! + 4! В 18
- 3*3! - 32 Г 72
Д 144
2. Встановити відповідність між заданими позначеннями кількостей сполук та їх числовими значеннями
- С72 А 5
- С59 Б 52
- С710 : Р4 В 28
- А28 – С28 Г 21
Д 126
Варіант 4
1. Встановити відповідність між виразами та їх значеннями
-
 А 126
А 126
-
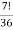 Б 30
Б 30
- 3! + 5! В 114
- 5! - 6 Г 140
Д 124
2. Встановити відповідність між заданими позначеннями кількостей сполук та їх числовими значеннями
- А72 А 8
- С46 Б 7
- С39 : А42 В 42
- С28 - Р4 Г 15
Д 4
Елементи теорії ймовірностей і математичної статистики
Варіант 1
- Ряд даних вибірки має вигляд : 2, 8, 4, 5, 2, 6, 5, 4, 2. Встановити відповідність між заданими статистичними характеристиками ряду даних та їх значеннями
-
Розмах вибірки А 4

- Мода Б 2
- Медіана В 4
- Середнє значення Г 6
Д 4![]()
- У ящику є 6 червоних, 8 синіх, 12 зелених і 14 білих куль. Встановити відповідність між заданими подіями та їхніми ймовірностями
-
Перша навмання вийнята куля – червона або біла. А
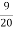
-
Перша навмання вийнята куля – червона або зелена. Б

-
Перша навмання вийнята куля – не червона . В
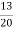
-
Перша навмання вийнята куля – не біла. Г
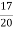
Д ![]()
Варіант 2
1. Ряд даних вибірки має вигляд : 7, 5, 4, 6, 4, 3, 9, 4, 5. Встановити відповідність між заданими статистичними характеристиками ряду даних та їх значеннями
-
Розмах вибірки А 5

- Мода Б 5
- Медіана В 4
- Середнє значення Г 6
Д 6![]()
- У ящику є 5 червоних, 8 синіх, 7 зелених і 10 жовтих куль. Встановити відповідність між заданими подіями та їхніми ймовірностями
-
Перша навмання вийнята куля – червона або зелена. А

-
Перша навмання вийнята куля – не жовта. Б

- Перша навмання вийнята куля – біла . В 0
-
Перша навмання вийнята куля – червона. Г

Д ![]()
Варіант 3
- Ряд даних вибірки має вигляд : 5, 4, 3, 8, 8, 12, 8, 4, 5. Встановити відповідність між заданими статистичними характеристиками ряду даних та їх значеннями
-
Розмах вибірки А 4

- Мода Б 9
- Медіана В 8
- Середнє значення Г 5
Д 6![]()
2. У ящику є 8 червоних, 5 чорних, 7 зелених і 10 білих куль. Встановити відповідність між заданими подіями та їхніми ймовірностями
-
Перша навмання вийнята куля – біла. А
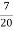
-
Перша навмання вийнята куля – червона або чорна. Б
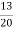
-
Перша навмання вийнята куля – не чорна . В

-
Перша навмання вийнята куля – не біла. Г

Д ![]()
Варіант 4
1. Ряд даних вибірки має вигляд : 7, 10,14, 13, 11, 14, 10, 14, 15. Встановити відповідність між заданими статистичними характеристиками ряду даних та їх значеннями
- Розмах вибірки А 14
- Мода Б 8
- Медіана В 12
- Середнє значення Г 13
Д 16
2. У ящику є 11 червоних, 8 синіх, 8 білих і 13 оранжевих куль. Встановити відповідність між заданими подіями та їхніми ймовірностями
-
Перша навмання вийнята куля – червона або оранжева. А

-
Перша навмання вийнята куля – не синя. Б

-
Перша навмання вийнята куля – біла . В

-
Перша навмання вийнята куля – синя або біла. Г

Д ![]()
Похідна функції
Варіант 1
- Встановити відповідність між функціями та їх похідними
- у = - 4х -5 А у' = 5
-
у = - 4 + 5х Б у' =

-
у =
 + 5 В у' = - 4
+ 5 В у' = - 4
-
у =
 - 4 Г у' = - 5
- 4 Г у' = - 5
Д у' = ![]()
- Встановити відповідність між функціями та їх похідними
- у = cos (3x+4) А у' = 4cos (4x - 5)
- у = sin (4x - 5) Б у' = -3 sin (3x + 4)
- у = 3 cos (x+4) В у' = 4cos (x + 5)
- у = 4 sin (x + 5) Г у' = cos (3x+4)
Д у' = -3sin (x +4)
- Встановити відповідність між функціями та їх похідними в точці х0 = 1
-
у = 3х2 + 5х А 9

- у = - 10 + 5х4 Б 10
-
у =
 + 3х3 В - 8
+ 3х3 В - 8
-
у =
 – 4х2 Г 9
– 4х2 Г 9
Д - 7![]()
Варіант 2
- Встановити відповідність між функціями та їх похідними
- у = 3х + 6 А у' = -3
-
у = - 4 - 3х Б у' = -

-
у = -
 + 5 В у' = 3
+ 5 В у' = 3
-
у =
 - 3 Г у' = - 5
- 3 Г у' = - 5
Д у' = ![]()
- Встановити відповідність між функціями та їх похідними
- у = cos (4x+6) А у' = -5cos (5x - 3)
- у = -sin (5x - 3) Б у' = -4 sin (4x + 6)
- у = 3 cos (x+6) В у' = -3sin (x + 6)
- у = 4sin (x + 3) Г у' = -4cos (4x+6)
Д у' = 4cos (x +3)
- Встановити відповідність між функціями та їх похідними в точці х0 = 2
-
у = 4х2 + 5х А 20

- у = - 10 + 3х3 Б 21
-
у =
 + 5х2 В - 11
+ 5х2 В - 11
-
у =
 – 3х2 Г 9
– 3х2 Г 9
Д 26
Варіант 3
- Встановити відповідність між функціями та їх похідними
- у = 7х + 6 А у' = - 7
-
у = - 5х + 7 Б у' = -

-
у =
 + 5 В у' = 7
+ 5 В у' = 7
-
у =-
 + 4 Г у' = - 5
+ 4 Г у' = - 5
Д у' = ![]()
2. Встановити відповідність між функціями та їх похідними
- у = 8cos (5x+3) А у' = 8cos (8x - 3)
- у = sin (8x - 3) Б у' = -8 sin (8x - 3)
- у = -5 cos (8x - 3) В у' = - 7cos (x + 7)
- у = -7 sin (x + 7) Г у' = - 40 sin (5x+3)
Д у' = 40sin (8x - 3)
3. Встановити відповідність між функціями та їх похідними в точці х0 = - 1
-
у = 7х2 + 8х А -15

- у = 9х3 + 6х2 Б 15
-
у =
 х2 - 5х3 В - 6
х2 - 5х3 В - 6
-
у =
 х3 – 4х Г -3
х3 – 4х Г -3
Д - 4![]()
Варіант 4
1. Встановити відповідність між функціями та їх похідними
- у = 3х - 4 А у' = -4
-
у = - 4х + 3 Б у' = -

-
у =
 - 5 В у' = 3
- 5 В у' = 3
-
у = -
 + 7 Г у' = - 4
+ 7 Г у' = - 4
Д у' = ![]()
2. Встановити відповідність між функціями та їх похідними
- у = - 5cos (4x- 3) А у' = -20 sin (5x - 3)
- у = 5sin (3x - 4) Б у' = -20 sin (4x - 3)
- у = 4 cos (5x - 3) В у' = 20sin (4x - 3)
- у = -3sin (5x + 4) Г у' = 15cos (3x - 4)
Д у' = -15cos (5x +4)
3. Встановити відповідність між функціями та їх похідними в точці х0 = - 2
- у = 2х2 + 7х А - 5
- у = х3 - 2х Б 10
- у = - 8 + 4х2 В - 1
-
у =
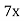 – х3 Г 8
– х3 Г 8
Д - 16
Геометричний та фізичний зміст похідної
Варіант 1
- Встановити відповідність між функціями та кутовими коефіцієнтами дотичної до графіка цієї функції з абсцисою х0
- f(х) = х3, х0 = 2 А 1
-
f(х) =
 , х0 = -1 Б 12
, х0 = -1 Б 12
- f(х) = х2 +2, х0 = 4 В -1
-
f(х) =
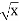 , х0 =
, х0 =  Г 8
Г 8
Д 2
- Встановити відповідність між залежностями відстані s від часу t руху матеріальних тіл та їх швидкостями в момент часу t = 2с
- s(t) = 6t – t2 А 24м/с
- s(t) = t3 + 3t2 Б 16м/с
-
s(t) = 6t – 2t2 +
 t3 В 8м/с
t3 В 8м/с
- s(t) = 3t2 – 4t + 2 Г 2м/с
Д 4м/с
Варіант 2
- Встановити відповідність між функціями та кутовими коефіцієнтами дотичної до графіка цієї функції з абсцисою х0
- f(х) = х3 + 4, х0 = 1 А -4
-
f(х) =
 , х0 =
, х0 =  Б 6
Б 6
- f(х) = х2 +5, х0 = 3 В -1
-
f(х) =
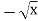 , х0 =
, х0 =  Г 8
Г 8
Д 3
- Встановити відповідність між залежностями відстані s від часу t руху матеріальних тіл та їх швидкостями в момент часу t = 1с
-
s(t) =
 t4 + 8t2 А 17м/с
t4 + 8t2 А 17м/с
-
s(t) =
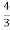 t3 - 2t Б 2м/с
t3 - 2t Б 2м/с
- s(t) = 6 – 2t2 + 3t3 В 7м/с
-
s(t) =
 t5 + 6t3 – 4t Г 5м/с
t5 + 6t3 – 4t Г 5м/с
Д 18м/с
Варіант 3
1. Встановити відповідність між функціями та кутовими коефіцієнтами дотичної до графіка цієї функції з абсцисою х0
- f(х) = х4, х0 = 1 А 9
-
f(х) = -
 , х0 = 3 Б 4
, х0 = 3 Б 4
-
f(х) = 3х3, х0 = - 1 В

-
f(х) =
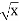 , х0 = 4 Г
, х0 = 4 Г 
Д - ![]()
2. Встановити відповідність між залежностями відстані s від часу t руху матеріальних тіл та їх швидкостями в момент часу t = 2с
- s(t) = 7t2 – 4 А 12м/с
- s(t) = 2t3 - 4t Б 50м/с
- s(t) = 5t2 – 4t +8 В 26м/с
-
s(t) =
 t3 +
t3 +  t2 + 7 Г 15м/с
t2 + 7 Г 15м/с
Д 42м/с
Варіант 4
1. Встановити відповідність між функціями та кутовими коефіцієнтами дотичної до графіка цієї функції з абсцисою х0
- f(х) = 2х3 , х0 = - 1 А -6
- f(х) = 2х4, х0 = 1 Б 6
-
f(х) = - 6х2 , х0 =
 В -2
В -2
-
f(х) =
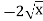 , х0 = 4 Г 8
, х0 = 4 Г 8
Д - ![]()
2. Встановити відповідність між залежностями відстані s від часу t руху матеріальних тіл та їх швидкостями в момент часу t = 1с
- s(t) = 3t2 - 8t А 6м/с
-
s(t) = - 10t +
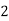 t2 Б 30м/с
t2 Б 30м/с
-
s(t) = -3t +
 t3 В 16м/с
t3 В 16м/с
- s(t) = 6t2 – 18t Г 24м/с
Д 13м/с
Застосування похідної для дослідження функцій
Варіант 1
- Встановити відповідність між похідними f '(х) функцій та проміжками зростання відповідних їм функцій f (х)
- f '(х) = (х -4)2(х+2) А [- 4; 2]
- f '(х) = (2-х)(х+4) Б [ -2; ∞)
- f '(х) = (х -4)(х-2)2 В ( - ∞; -4]U[ -2; ∞)
- f '(х) = (х +4)(х+2) Г [ 4; ∞)
Д ( - ∞; 2]U[ 4; ∞)
- Встановити відповідність між похідними f '(х) функцій та проміжками спадання відповідних їм функцій f (х)
1. f '(х) = (х +3)(х-1) А [1; ∞)
2. f '(х) = (1-х)(3 - х)2 Б [ -1; 3]
3. f '(х) = (х + 1)(х-3) В ( - ∞; 1]
4. f '(х) = (х +3)2(х-1) Г ( - ∞; -1]
Д [ - 3; 1]
- Встановити відповідність між функціями та їх критичними точками
- у = 8х + х2 А 1; -1; 0
- у = х2 - 4 Б 2
- у = х2 - 6х В 0; - 1;
- у = х4 - 2х2 Г 3
Д - 4
Варіант 2
- Встановити відповідність між похідними f '(х) функцій та проміжками зростання відповідних їм функцій f (х)
- f '(х) = (х -5)(х+7) А [- 5; ∞)
- f '(х) = (5-х)(х+7) Б [ -7; 5]
- f '(х) = (х -5)2(х-7) В ( - ∞; -7]U[ 5; ∞)
- f '(х) = (х +5)(х+7)2 Г [ 7; ∞)
Д ( - ∞; -5]U[ 7; ∞)
- Встановити відповідність між похідними f '(х) функцій та проміжками спадання відповідних їм функцій f (х)
1. f '(х) = (х -4)2(х+8) А [- 8; ∞)
2. f '(х) = (8-х)(4 - х) Б [ 4; 8]
3. f '(х) = (х - 8)(х+4)2 В ( - ∞; -8]
4. f '(х) = (х +4)(х+8) Г ( - ∞; 8]
Д [ - 8; -4]
- Встановити відповідність між функціями та їх критичними точками
- у = х4 - 4х А 1; -1
- у = 2х4 - х2 Б 1
-
у = х2 + 6х В 0; -
 ;
; 
- у = х3 - 3х Г -3
Д -1
Варіант 3
1. Встановити відповідність між похідними f '(х) функцій та проміжками зростання відповідних їм функцій f (х)
- f '(х) = (х - 4)(х + 3) А [- 3; ∞]
- f '(х) = (х - 3)2(х + 4) Б [ - 4; ∞)
- f '(х) = (х - 4)2(х + 3) В ( - ∞; -3]U[ 4; ∞)
- f '(х) = (х - 4)(х - 3) Г [ 4; ∞)
Д ( - ∞; 3]U[ 4; ∞)
2. Встановити відповідність між похідними f '(х) функцій та проміжками спадання відповідних їм функцій f (х)
1. f '(х) = (х + 5)(х + 1)2 А [1; 5]
2. f '(х) = (1 - х)(5 - х) Б [ 1; - 5]
3. f '(х) = (х - 1)(7 - х)2 В ( - ∞; 1]
4. f '(х) = (х +1)(х-5) Г ( - ∞; -5]
Д [ - 1; 5]
3. Встановити відповідність між функціями та їх критичними точками
- у = 3х3 - 9х А 1; -1; 0
- у = 6х2 – 2х Б -1; 1
- у = 3х4 - 6х2 В 0; - 1;
-
у = х4 – х3 Г 0;

Д ![]()
Варіант 4
1. Встановити відповідність між похідними f '(х) функцій та проміжками зростання відповідних їм функцій f (х)
- f '(х) = (х - 6)(х + 5) А [ 5; ∞)
- f '(х) = (х - 5)(х + 6)2 Б [ 6; ∞]
- f '(х) = (х + 5)2(х - 6) В ( - ∞; -5]U[ 6; ∞)
- f '(х) = (х + 6)(х - 5) Г [ - ∞; -6]
Д ( - ∞; -6]U[ 5; ∞)
2. Встановити відповідність між похідними f '(х) функцій та проміжками спадання відповідних їм функцій f (х)
1. f '(х) = (х + 2)2( х - 3) А [ 2; ∞)
2. f '(х) = (3-х)( х + 2) Б [ - 2; 3]
3. f '(х) = (2 - х)(х+3)2 В ( - ∞; -2] U[ 3; ∞)
4. f '(х) = (х - 2)(х + 3) Г ( - ∞; 3]
Д [ - 3; 2]
3. Встановити відповідність між функціями та їх критичними точками
- у = х4 + 2х2 А -1
- у = 2х3 - 3х2 Б 0
-
у = 3х2 + 6х В

- у = х2 - 8х Г -1; 0
Д 0; 1
Первісна. Правила знаходження первісної
Варіант 1
- Встановити відповідність між функціями f(х) та їх первісними F(х)
- f(х) = х3 А F(x) = х3 + С
-
f(х) =
 х3 Б F(x) =
х3 Б F(x) =  х4 + С
х4 + С
-
f(х) = 3х2 В F(x) =
 х4 + С
х4 + С
-
f(х) =
 х2 Г F(x) = 8х3 + С
х2 Г F(x) = 8х3 + С
Д F(x) = ![]() х3 + С
х3 + С
- Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = cos 7х + sin
 А F(x) =
А F(x) =  sin7х -
sin7х - 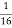 cos 4х + C
cos 4х + C
-
f(х) = cos 7х + 7sin х Б F(x) = 4sin х -
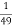 cos 7х + C
cos 7х + C
-
f(х) = 4cos х +
 sin 7х В F(x) =
sin 7х В F(x) =  sin7 х - 7cos х + C
sin7 х - 7cos х + C
-
f(х) = cos 7х +
 sin 4х Г F(x) = 7sin х - cos 7х + C
sin 4х Г F(x) = 7sin х - cos 7х + C
Д F(x) = = ![]() sin7 х - 7cos
sin7 х - 7cos ![]() + C
+ C
- Встановити відповідність між точками і первісними F(х), графік яких проходить через дані точки, для функції f (х) = х2 +5
-
М (-1; -1) А F(x) = х3/3 + 5х + 5

-
М (1;1) Б F(x) = х3/3 +5х - 4

-
М (1; 0) В F(x) = х3/3 + 5х - 5

-
М(-1; 0) Г F(x) = х3/3 + 5х + 4

Д F(x) = х3/3 + 5х - ![]()
Варіант 2
- Встановити відповідність між функціями f(х) та їх первісними F(х)
- f(х) = х3 А F(x) = х3 + С
-
f(х) =
 х3 Б F(x) =
х3 Б F(x) = 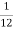 х4 + С
х4 + С
-
f(х) = 6х2 В F(x) =
 х4 + С
х4 + С
-
f(х) =
 х2 Г F(x) = 2х3 + С
х2 Г F(x) = 2х3 + С
Д F(x) = ![]() х3 + С
х3 + С
- Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = cos 4х + sin
 А F(x) = sin
А F(x) = sin - cos 4х + C
- cos 4х + C
-
f(х) = cos
 + sin 4х Б F(x) = sin 4х - cos
+ sin 4х Б F(x) = sin 4х - cos  + C
+ C
-
f(х) =
 cos
cos + 4sin 4х В F(x) = 16sin4х -
+ 4sin 4х В F(x) = 16sin4х - 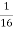 cos
cos + C
+ C
-
f(х) = 4 cos 4х +
 sin
sin  Г F(x) = 4sin
Г F(x) = 4sin  - 4cos
- 4cos + C
+ C
Д F(x) = = 4sin![]() -
- ![]() cos4х + C
cos4х + C
- Встановити відповідність між точками і первісними F(х), графік яких проходить через дані точки, для функції f (х) =3х2 + 4х
- М (-1; -1) А F(x) = х3 + 2х2 - 5
- М (2; 1) Б F(x) = х3 + 2х2 - 2
- М (1; -2) В F(x) = х3 + 2х2 +1
- М(-2; 1) Г F(x) = х3 + 2х2 -15
Д F(x) = х3 + 2х2 -1
Варіант 3
1. Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = 5х4 А F(x) =
 х3 + С
х3 + С
- f(х) = 3 х2 Б F(x) = 2х4 + С
- f(х) = 8х3 В F(x) = х4 + С
-
f(х) =
 х2 Г F(x) = х5 + С
х2 Г F(x) = х5 + С
Д F(x) = х3 + С
2. Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = sin5x + cos
 А F(x) =
А F(x) =  sin5х - 5cos
sin5х - 5cos  + C
+ C
-
f(х) = sin
 + cos5х Б F(x) = 5sin
+ cos5х Б F(x) = 5sin  +
+  cos5х + C
cos5х + C
-
f(х) =
 sin5х +
sin5х +  cosх В F(x) =-
cosх В F(x) =-  cos5х + 5sin
cos5х + 5sin + C
+ C
-
f(х) = sin
 + 4cosх Г F(x) = 4sinх - 5cos
+ 4cosх Г F(x) = 4sinх - 5cos + C
+ C
Д F(x) = = ![]() sinх -
sinх - ![]() cos5x + C
cos5x + C
3. Встановити відповідність між точками і первісними F(х), графік яких проходить через дані точки, для функції f (х) = х3 - 1
-
М (-1; -1) А F(x) = х4/4 - х - 2

-
М (1;1) Б F(x) = х4/4 - х +

-
М (1; 0) В F(x) = х4/4 - х + 1

-
М(-1; 0) Г F(x) = х4/4 - х - 2
 Д F(x) = х4/4 - х - 1
Д F(x) = х4/4 - х - 1
Варіант 4
1. Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = х4 А F(x) =
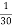 х6 + С
х6 + С
-
f(х) =
 х5 Б F(x) =
х5 Б F(x) =  х3 + С
х3 + С
-
f(х) = 4х3 В F(x) =
 х5 + С
х5 + С
-
f(х) =
 х2 Г F(x) = х4 + С
х2 Г F(x) = х4 + С
Д F(x) = ![]() х6 + С
х6 + С
2. Встановити відповідність між функціями f(х) та їх первісними F(х)
-
f(х) = cos
 + sin5x А F(x) = sin5x - cos
+ sin5x А F(x) = sin5x - cos + C
+ C
-
f(х) = cos5x + sin
 Б F(x) = 5sin
Б F(x) = 5sin -
-  cos5x + C
cos5x + C
-
f(х) = 5cos5x +
 sin
sin В F(x) = 5cos5х -
В F(x) = 5cos5х -  sin5x + C
sin5x + C
-
f(х) =
 cos
cos + 5sin5x Г F(x) = sin
+ 5sin5x Г F(x) = sin  – cos5x + C
– cos5x + C
Д F(x) = = ![]() sin5x - 5cos
sin5x - 5cos![]() + C
+ C
3. Встановити відповідність між точками і первісними F(х), графік яких проходить через дані точки, для функції f (х) =2х3 - 2х
-
М (-1; -1) А F(x) =
 х4 - х2 - 3
х4 - х2 - 3
-
М (2; 1) Б F(x) =
 х4 - х2 - 5
х4 - х2 - 5
-
М (1; -2) В F(x) =
 х4 - х2 - 6
х4 - х2 - 6
-
М(-2; -1) Г F(x) =
 х4 - х2 -
х4 - х2 -  Д F(x) =
Д F(x) =  х4 - х2 - 1
х4 - х2 - 1
Визначений інтеграл. Формула Ньютона-Лейбніца
Варіант 1
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
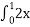 3 dx А 1
3 dx А 1
-
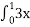 2 dx Б
2 dx Б 
-
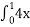 5 dx В
5 dx В 
-
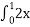 4 dx Г
4 dx Г 
Д ![]()
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
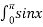 dx А 4
dx А 4
-
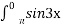 dx Б -
dx Б - 
-
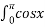 dx В 2
dx В 2
-
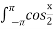 dx Г
dx Г 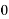
Д ![]()
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
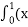 2-1) dx А
2-1) dx А 
-
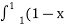 2)dx Б -
2)dx Б - 
-
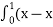 2) dx В
2) dx В 
-
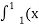 2-х) dx Г
2-х) dx Г 
Д ![]()
Варіант 2
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
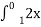 2 dx А -1
2 dx А -1
-
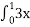 4 dx Б
4 dx Б 
-
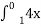 3 dx В
3 dx В 
-
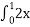 5 dx Г
5 dx Г 
Д ![]()
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
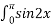 dx А 4
dx А 4
-
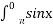 dx Б - 2
dx Б - 2
-
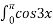 dx В 2
dx В 2
-
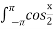 dx Г
dx Г 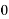
Д ![]()
- Встановити відповідність між визначеними інтегралами та їх значеннями
-
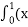 2- 4) dx А 7
2- 4) dx А 7 
-
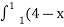 2)dx Б - 3
2)dx Б - 3 
-
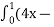 1) dx В
1) dx В 
-
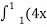 – х2) dx Г 1
– х2) dx Г 1
Д - ![]()
Варіант 3
1. Встановити відповідність між визначеними інтегралами та їх значеннями
-
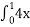 4 dx А
4 dx А 
-
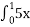 3 dx Б
3 dx Б 
-
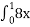 5 dx В
5 dx В 
-
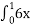 3 dx Г
3 dx Г 
Д ![]()
2. Встановити відповідність між визначеними інтегралами та їх значеннями
-
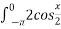 dx А 4
dx А 4
-
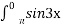 dx Б -
dx Б - 
-
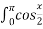 dx В - 2
dx В - 2
-
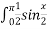 dx Г
dx Г 
Д 2
3. Встановити відповідність між визначеними інтегралами та їх значеннями
-
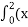 2- x)dx А -4
2- x)dx А -4
-
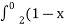 2)dx Б -
2)dx Б - 
-
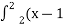 )dx В -
)dx В - 
-
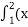 – х2) dx Г
– х2) dx Г 
Д ![]()
Варіант 4
1. Встановити відповідність між визначеними інтегралами та їх значеннями
-
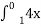 3 dx А -1
3 dx А -1
-
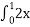 2 dx Б
2 dx Б 
-
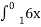 4 dx В
4 dx В 
-
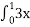 5 dx Г
5 dx Г 
Д ![]()
2. Встановити відповідність між визначеними інтегралами та їх значеннями
-
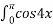 dx А -
dx А - 
-
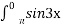 dx Б 2
dx Б 2
-
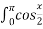 dx В - 2
dx В - 2
-
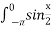 dx Г
dx Г 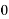
Д ![]()
3. Встановити відповідність між визначеними інтегралами та їх значеннями
-
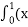 2- 3x) dx А 5
2- 3x) dx А 5 
-
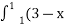 2)dx Б 6
2)dx Б 6 
-
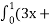 1) dx В -1
1) dx В -1
-
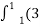 + х2) dx Г 2
+ х2) dx Г 2
Д 5 ![]()
1


про публікацію авторської розробки
Додати розробку
