Урок "Прес - конференція банку" на тему: "Правила знаходження первісних"

Про матеріал

Дидактичний матеріал до нестандартного уроку (прес - конференція банку) на тему "Правила знаходження первісних", та опорний конспект до теми "Первісна та її властивості".

Перегляд файлу

Мета:

Навчальна: закріпити знання про первісну, формувати в учнів вміння і навички обчислення первісних, користуючись таблицею первісних та правилами знаходження первісних.

Розвиваюча: розвивати вміння самостійно використовувати набуті знання, активізувати пізнавальну діяльність.

Виховна: формувати навички правильної математичної мови.

Тип уроку: урок закріплення і удосконалення нових знань, умінь і навичок.

Вид уроку: прес – конференція банку.

Конструктор уроку:

І. Організаційна частина.

ІІ. Перевірка домашнього завдання.

• Бліцопитування;

• сигнальні картки; картки – завдання.

ІІІ. Актуалізація знань, умінь і навичок.

• Інтерактивна гра «Прес - конференція»;  самостійний творчий пошук учнів: - газета «Банківська справа»;

- журнал «Історія і право»;

- телепередача «Успішний бізнесмен»; - газета «Аргументи і факти».

• тестові завдання; картки – завдання.

IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

• «Самооцінка» своєї готовності до уроку.

V. Сприйняття та усвідомлення нового матеріалу.

• опорний конспект.

VІ. Перевірка знань учнями фактичного матеріалу.

• Стратегія творчого пошуку учнів:

- видавництво «Шпаргалка студенту»;

- телепередача «Віриш? Не віриш?»; - видавництво «Екзамен без проблем»;  картки – завдання.

VІІ. Підведення підсумків. Домашнє завдання.

• Радіопередача «Роблю сам»

Бліцопитування

(перевірка домашнього завдання)

Початковий рівень

(за кожну правильну відповідь – 1 бал)

Відімкніть кодовий замок банку «Первісна»

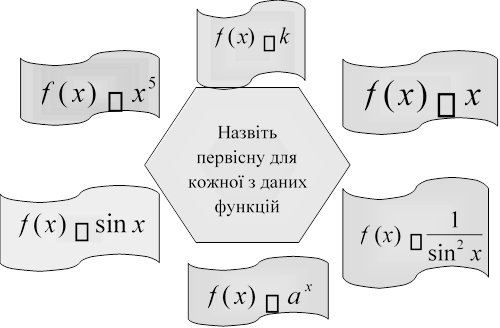
«Прес - конференція»

(актуалізація) Середній рівень

(за кожну правильну відповідь – 1 бал)

Дайте відповіді на запитання журналістів із різних науково – популярних газет, журналів телепередач тощо

Тестові завдання

(картка – завдання №1)

Початковий рівень

(за кожну правильну відповідь – 1 бал)

1. Яка з наведених функцій є первісною функції f (x) = x⁴?

А) F(x) = 4x³; Б) F(x) =; B) F(x) _^x⁵; Г) F(x) = x⁵.

2. Знайдіть загальний вигляд первісної функції f (x) = x – 4:

А) x² – 4x + C; Б) 4x + C; В) ; Г) x²– 4 + C.

3. 3. Укажіть загальний вигляд первісної функції f (x) = 2x³+ 6x: А) 6x + 6 + C; Б) ¹x⁴_3x²_c; В) x⁴ + 2x³+ C; Г) 4x⁴ + 3x² + C.

Тестові завдання

(картка – завдання №2)

Середній рівень

(за кожну правильну відповідь – 1 бал)

4. Яка з поданих функцій є первісною функції f (x) = 3^x?

А) ; Б) F(x) = 3^xln3; В) F(x) = 3^x; Г) F(x) _³^x

5. 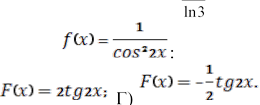Яка з наведених функцій є первісною функції

A) Б) В)

6. Укажіть загальний вигляд первісної функції f(x) = 10x⁴ - 6x.

А) 2x⁵ – 4x² + C; Б) 2x⁵ – 3x² + C; В) 5x⁵ – 4x² + C; Г) 40x³ – 6 + C.

*Правильні відповіді відмітьте* X		А	Б	В	Г		А	Б	В	Г
	1					4
	2					5
	3					6

Мотивація «Самооцінка» своєї готовності до уроку

Дайте відповіді на запитання:

- Хто сьогодні готовий отримати найвищу оцінку?

- Хто добре готовий до уроку?

- Хто не готовий?

«Опорний конспект»

на тему: «Правила знаходження первісних»

Правила знаходження первісних (правила інтегрування)

1. Якщо F — первісна для f, а G — первісна для g, то F + G — первісна для f + g. Первісна для суми дорівнює сумі первісних для доданків.

1. ∫(f (x) + g(x))dx= ∫ f(x) dx+ ∫ g(x) dx

Інтеграл від суми дорівнює сумі інтегралів від доданків.

2. Якщо F — первісна для f і с — стала, то сF — первісна для функції сf.

2. ∫c f (x) dx = c ∫ f (x) dx,

де c — стала.

Сталий множник можна виноси_ ти за знак інтеграла.

3. Якщо F — первісна для f, а k і b— сталі (причому k ≠ 0), то

¹F (kx + b )— первісна для k функції f (kx + b).

3. ∫ f (kx+ b) dx = ¹ F( kx+ b) + C. k

«Прес - конференція»

(закріплення нового матеріалу) Початковий рівень

(за правильну відповідь – 3 бали)

«Опорний конспект»

на тему: «Первісна та її властивості»

1. Невизначений інтеграл

Означення

Приклад

Сукупність усіх первісних для да_ ної функції f (x) називається невиз_ наченим інтегралом і позначаєть_ ся символом _f (x) dx, тобто

_f (x) dx = F(x) + C,

де F (x) — одна з первісних для

функції f (x), а C — довільна стала.

3 x

 x dx c,

оскільки для функції f x x³ на інтервалі; всі первісні можна x4

записати так: С

2. Правила знаходження первісних (правила інтегрування)

1. Якщо F — первісна для f, а G — первісна для g, то F + G — первісна для f + g.

Первісна для суми дорівнює сумі первісних для доданків.

1. ∫(f (x) + g(x))dx= ∫ f(x) dx+ ∫ g(x) dx

Інтеграл від суми дорівнює сумі інтегралів від доданків.

2. Якщо F — первісна для f і с — стала, то сF — первісна для функції сf.

2. ∫c f (x) dx = c ∫ f (x) dx,

де c — стала.

Сталий множник можна виноси_ ти за знак інтеграла.

3. Якщо F — первісна для f, а k і b— сталі (причому k ≠ 0), то

¹F (kx + b )— первісна для k функції f (kx + b).

3. ∫ f (kx+ b) dx = ¹ F( kx+ b) + C. k

«Опорний конспект»

на тему: «Первісна та її властивості»

Таблиця первісних (невизначених інтегралів)
Функція f (x)	*Загальний вигляд первісних F (x) + C, де С – довільна стала*	Запис за допомогою невизначеного інтеграла
0	С	 0dxC
1	Х+С	_dxxC
_х^(1)	x1 C 1	x1 _x^dx ₁C (1) 
1 х	ln xC	dx _x ln x C
sin x	cosxC	sin xdxcosxC
сosx	sin xC	_cosxdxsin xC
1 cos²x	tgxC	dx  ₂xtgxC cos
1 sin²x	ctgxC	dx  ₂x ctgxC sin
ex	e^xС	e^xdxe^xC
ах (0,1)	ax C  ln a	a^xdx_^ax C ln a