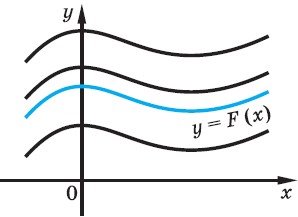
Урок - лекція на тему: "Первісна та її властивості"

Про матеріал

Дидактичний матеріал до нестандартног уроку - лекції на тему: "Первісна та її властивості".

Перегляд файлу

Мета:

Навчальна: сформувати в учнів поняття первісної для функції та її основної властивості.

Розвиваюча: розвивати логічне мислення, пам'ять, увагу, математичну грамотність.

Виховна: виховувати акуратність, наполегливість, інтерес до вивчення математики.

Тип уроку: засвоєння нових знань.

Вид уроку: урок - лекція.

Конструктор уроку:

І. Організаційна частина.

ІІ. Перевірка домашнього завдання.

• Бліцопитування «Ланцюжком».

ІІІ. Актуалізація знань, умінь і навичок.

• Інтелектуальна розминка «Гра - змагання»;  картки - завдання.

IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

• «Відстрочена загадка».

V. Сприйняття та усвідомлення нового матеріалу.

• Опорний конспект на тему «Первісна та її властивості»;  Приклади розв’язання завдань.

VІ. Осмислення нового матеріалу.

• Стратегія творчого пошуку «Інтелектуальний тир»

VІІ. Підведення підсумків.

• Бліцопитування «Шерлок Холмс»

VІІІ. Підведення підсумків. Рефлексія.

• Смайлики (рефлексія викладача);

• «Квітка засвоєння» (рефлексія учнів)

ІX. Домашнє завдання.

• Обов’язковий мінімум;  тренувальні завдання;  творчі завдання.

Бліцопитування «Ланцюжком»

(перевірка домашнього завдання)

Початковий рівень

(за кожну правильну відповідь – 1 бал)

1. Що називають похідною даної функції?

2. Назвіть похідні елементарних функцій.

3. Які правила обчислення похідних ви знаєте?

4. Назвіть функцію, похідна якої дорівнює:

а) x²; б) _sin x; в) ¹; г) ¹.

x 2 x

5. Назвіть дві функції, похідні яких дорівнюють:

а) ₂; б) e^x; в) cosx.

сos x

Інтелектуальна розминка «Гра – змагання»

(картка – завдання №1) Середній рівень

(за кожну правильну відповідь – 1 бал)

Знайдіть похідні записаних функцій. Хто якісніше, раціональніше і швидше його виконає, той отримує додаткові 2 бали до оцінки за урок.

а) у = 4х + 6;

б) у = х^-5;

в) у = – 12х ;

г) у = cos (4х) – 3;

д) у = tg 6x – ctg 8.

Розв’язання:

Інтелектуальна розминка «Гра – змагання»

(картка – завдання №2) Середній рівень

(за кожну правильну відповідь – 1 бал)

а) у = у = х⁵ – 7х;

б) у = (6х)³;

в) у = ( 7х) ^{– 3};

г) у = sіn (4х) + 3;

д) у = сtg 6x – tg 8.

Розв’язання:

«Відстрочена загадка»

(мотивація)

1. Яка дія обернена до додавання; віднімання; ділення; множення; піднесення до степеня; логарифмування?

2. Яка операція буде оберненою до операції диференціювання функції?

3. Чи можна, знаючи миттєву швидкість руху t точки, визначити пройдений нею шлях St^?

Опорний конспект

на тему: «Первісна та її властивості»

1. Первісна
Означення	Приклад
*Функція F (x) називається первіс_ ною для функції f (x) на даному* *проміжку, якщо для будь-якого x з цього проміжку* Fx f x.	Для функції f x x³ на інтервалі; первісною є x4 функціяFx , 4   x4  1 3 x3 оскількиFx  _4 _ 4 4 x 
2. Основна властивість первісної
Властивість	Геометричний зміст
Якщо функція F (x) є первісною для функції f (x) на даному проміжку,а C — довільна стала, то функціяF (x) + C також є первісною для функції f (x), при цьому будь-яка первісна для функції f (x) на даному проміжку може бути записана у вигляді F (x) + C, де C — довільна стала. Приклад x4 Оскільки функціяFx є 4 первісною для функції f x x³ на інтервалі; (див. вище), то загальний вигляд усіх первісних для функції f x x³ можна записати так: ^x⁴С , де C — довільна стала. 4	Графіки будь_яких первісних для даної функції одержуються один з одного паралельним перенесен- ням уздовж осі Oy.

Приклади розв’язання завдань

Алгоритм розв’язання задачі

1.З’ясуй, про яке поняття йде мова в задачі.

2.Знайди в опорному конспекті необхідну формулу.

3.Підстав замість змінних їх числові значення згідно до умови. 4.Проведи обчислення.

5.Запиши відповідь.

Приклад 1

Перевірте, що функція F(x)  2 x є первісною для функції f (x)  ¹ на x

проміжку 0;.

Розв’язання Коментар

Fx 2 х  2 1  1 , а це й За означенням функція F (x) є

2 х х первісною для функції f (x), якщо

означає , що F (x) є Fx f x.

первісною для функції f (x)  .

Приклад 2 Для функції f (x)  х знайдіть первісну, графік якої проходить через точку M(9; 10).

Розв’язання Коментар

Спочатку запишемо загальний

Df  0;. Тоді f x x . вигляд первісних для заданої функ- Загальний вигляд усіх первісних для ції F(x) + C. Потім використаємо те, функції f (x) такий: що графік одержаної функції прохо-

x21 2 2 3 2 дить через точку M(9; 10), отже, при C  x C  x C  x x C x = 9 значення функції F (x) + C до-

1 3 3 3 рівнює 10. Щоб знайти первісну для

За умовою графік первісної прохо- функції f (x)  х , врахуємо, що об- дить через точку M(9; 10), отже, при ласть визначення цієї функції х0. x = 9 одержуємо 9 9 C 10. Тоді цю функцію можна записати

Звідси C = –8. Тоді шукана первісна: так: f x x і використати форму-

2 лу знаходження первісної для x x 8x. 1

3 функції _х_xα, а саме: х _С.

1

Початковий рівень

Смайлики (рефлексія викладача)

	*Молодці! Я вами задоволена.*
	*50 X 50*
	*Ви можете краще.*

«Квітка засвоєння» (рефлексія учнів)

Прикріпіть на дошці пелюстки квітки:

- Зелені – все зрозуміло;

- Сині – майже все зрозуміло;

- Жовті – зрозуміло наполовину;

- Оранжеві – дещо зрозуміло;

- Червоні – нічого не зрозуміло.

Домашнє завдання (диференційоване)

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 2

Оцінки та відгуки

Горик Руслана Миколаївна 19.11.2020 в 18:12

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Лук'янова Галина Юріївна 26.10.2020 в 11:35

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0