Розв’язування задач на обчислення ймовірності із застосуванням комбінаторних схем.

Тема: Розв’язування задач на обчислення ймовірності із застосуванням комбінаторних схем.

Урок математики у 11 класі

Мета:  -   працювати над формування умінь і навичок використання комбінаторних схем при розв’язування задач на знаходження ймовірностей; закріплення та систематизація знань по комбінаторні задачі, основні поняття теорії ймовірності та класичне означення ймовірності.

•         розвиток навичок побудови математичної моделі реальних процесів чи явищ, уміння аналізувати та систематизувати матеріал; уміння використовувати різні інформаційні джерела.
•         формувати життєві компетенції учнів.

Обладнання: комп’ютер, роздаткові картки.

Хід уроку

І. Мотивація начальної діяльності учнів. Оголошення мети і теми.

Учитель. «А чи можна виміряти міру впевненості числом? Звичайно, відповім я», - писав Блез Паскаль в своєму першому листі до П’єра Ферма 28 листопада 1654 р. Чому я назвала цих вчених? (Це одні із основоположників комбінаторики та теорії ймовірностей). Користуючись підручником, інтернет-ресурсом ви вже трішки знайомі з історією розвитку теорії ймовірності, сферами її застосування.

В яких сферах життя користуються методами комбінаторики та теорії ймовірності? (В криптографії, археології – кодування та розшифрування інформації, в біології – розшифровування будови ДНК, в хімії – комбінаторика дала можливість Д.І.Менделєєву розмістити хімічні елменти в таблицю, пізніше були перераховані всі ізомери, у фізиці – при виченні властивостей кристалів, опису моделі феромагнетизму). Оголошення теми. Мета, яку поставимо перед собою сьогодні на уроці? (відповіді учнів)

Учитель. Наша тема тісно пов’язана з життям. В математичному бюлетені, випущеному учнями класу було завдання - довести чи спростувати міфи.

ІІ. Актуалізація опорних знань.

1.     Доведення чи спростування міфів.

Міф 1. З кожною невдачею шанси підвищуються – так вважає більшість. Чим довше чекаєш автобус на зупинці або підвищення на роботі,  тим менше залишилось. Хто винен? Винен О.Бендер, що вбив в голову Кісі, а заодно і всім нам, що з кожним порожнім стільцем наші шанси зростають. І він правий, якщо мадам Петухова напевно сховала скарби під оббивкою. Якщо існує хоч один найменший в цьому сумнів, ситуація стає неприємною. З точки зору математики, якщо ймовірність події менше 100%, то і з кожною невдачею і сьогодні, і завтра – за правилом добутку ймовірність успіху зменшується.

Міф 2. Якщо шанси 50 на 50, виграти може хто завгодно. У своїй пропаганді казино враховують ймовірність виграшу в окремо обраній грі. Насправді, гарантовано перемагає той, у кого більше грошей. Щоб вигравати, потрібно грати в гру, де ймовірність виграшу 0,67 (2/3). Таких ігор немає. Тому казино треба залишати мільярдерам.

В 1992 р. група австралійських однодумців об’єдналася, щоб виграти в лотерею, в якій потрібно було вгадати 6 із 44 комбінацій – близько 7 млн. В результаті витративши по 2500 доларів і зафарбувавши всі можливі варіанти кожен учасник отримав по 9000 доларів, розподіливши виграш в 27 млн.

Міф 3. Тихіше ідеш – далі будеш. Відкриваючи свою справу, обережний підхід знижує шанси на сприятливий результат вчетверо, у порівняння з ризикованим підходом «поставити на кон все відразу». Вкладати в справу по гривні куди менше вигідно з точки зору теорії ймовірностей, ніж відразу вкласти мільйон.

2.     Яка сполука визначає, скількома способами класний керівник може розсадити 24 учня на 24 місця? (Перестановки).
3.     Після успішної здачі ЗНО 4 учні замовили машину для поїздки до моря. Водій запропонував їм безкоштовну поїздку, але тільки тоді, коли вони їздитимуть щорічно, пересідаючи так, щоб жоден варіант не повторювався. Через скільки років вони дочекаються безкоштовної поїздки? (24 роки – 4!).
4.     Яка сполука визначає, скількома способами можна розподілити:

а) три різні путівки між 11 учнями (розміщення).

б) три однакові путівки між 11 учнями? (комбінації).

5.     Подія А – Артур розв’язав всі задачі домашнього завдання, подія Б – Павло розв’язав всі задачі домашнього завдання.

а) у чому полягає подія А+Б? (Хоча б один з хлопців розв’язав всі задачі домашнього завдання).

б) у чому полягає подія АхБ? (Обидва точно розв’язали всі задачі домашнього завдання).

6.     Жили у бабусі два веселих гуся, один сірий, другий білий…

Яка ймовірність того, що навмання обраний гусь: а) білий (1/2); б) сірий (1/2); в) чорний (0); г) веселий (1).

ІІІ. Формування умінь та навичок.

Задача 1. На прибирання території виходять 12 учнів класу, серед яких 8 працюють якісно, 4 допускають брак.

1.     Яка ймовірність того, що навмання обраний учень буде працювати якісно?  Р(А) = 8/12 = 2/3 (обчислюється усно).
2.     Яка ймовірність того, що 3 навмання обраних учні будуть вмілими? Р(B) =
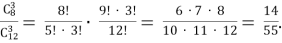
3.     Яка ймовірність того, що 2 учні будуть умілими, а 1 – допускає брак? Р(С) =

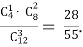
Задача 2. Є п’ять відрізків довжиною 1, 3, 4, 7 і 9 см. Визначити ймовірність того, що при трьох навмання відрізків (з даних п’яти) можна побудувати трикутник. (Р(А) = (Трикутник можна побудувати в двох випадках - 4, 7, 9 і 3, 7, і 9).

Учитель. Учні класу підготували добірку задач ЗНО, що стосуються даної теми.

Учень. Дослідивши завдання ЗНО, доводимо до вашої уваги їх підбірку. Серед всіх щорічних завдань ЗНО з даної теми зустрічається лише одне завдання і рівень його нескладний. Ось одне із них.

Задача 3. Кожну грань кубика пофарбували або в синій або в жовтий колір. Ймовірність того, що при підкиданні кубика випаде синя грань, дорівнює 1/3. Скільки всього граней кубика пофарбували в жовтий колір? В синій Р(А) = а/6 = 1/3; а = 2 – синій, тоді 6 – 2 = 4 (в жовтий).

або: в синій – 1/3, в жовтий 1 – 1/3 = 2/3, 2/3 від 6 – 4 грані.

або скористатись відповідями і перевірити їх всі.

Задача 4. На екзамен з математики виносять 80 питань. Учень підготував лише 55 з них. Білет складається з 4 питань. Яка ймовірність того, що учневі випадуть лише ті питання, які він підготував.

n = m = P(A) = .

Учитель. Чи достатньо цього для оцінки добре або відмінно? Висновок – треба вчити все.

ІV. Перевірка рівня засвоєння знань. Виконання тестової роботи.

http://sch4test.zzz.com.ua/

V. Підведення підсумків.

Учитель. Мудрець сказав: «Дві людини, які обмінялись золотими монетами, не стали багатими, але, якщо вони обмінялись думками, то кожний з них стає вдвоє багатшими. Адже обидва стали тепер розумнішими. Чи стали розумнішими ви?

Д/з. Повторити п. 28-30, п.17, №172 (4-6, 10-12).

Тест на banktestov.ru/test/?id=6465