Схема нарахування балів за виконання завдань контрольної роботи: 

1.    Завдання з вибором однієї правильної відповіді оцінюють у 0 або 1 бал: 1 бал, якщо вказано правильну відповідь; 0 балів, якщо вказано неправильну відповідь, або відповіді на завдання не надано.

2.    Завдання на встановлення відповідності («логічні пари») оцінюють у 1 бал за кожну правильно встановлену відповідність («логічну пару»); 0 балів за будь-яку «логічну пару», якщо зроблено більше однієї позначки в рядку. 

3.    Завдання відкритої форми з короткою відповіддюоцінюють у 0 або 2

бали: 2 бали, якщо вказано правильну відповідь; 0 балів, якщо вказано неправильну відповідь, або відповіді на завдання не надано. 

4.    Завдання відкритої форми з розгорнутою відповіддю оцінюють у 0, 1, 2, або 3 бали. Максимальну кількість балів учень отримує якщо навів усі етапи розв’язання й обґрунтував їх, зробив посилання на математичні факти, з яких випливає те чи інше твердження, проілюстрував розв’язання задачі рисунками, графіками тощо.

Таблиця відповідності тестових балів оцінкам 

Тема: Інтеграл та його застосування

Варіант І

Завдання 1-6 мають по п’ять варіантів відповідей, серед яких тільки ОДИН 

правильний. Виберіть  правильну, на вашу думку, відповідь та позначте її в бланку відповідей.

1. Знайдіть загальний вигляд первісної для функції 𝑓(𝑥) = 6𝑥⁵.

2.

3.

4. 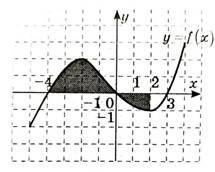      На рисунку зображено графік функції 𝑦 = 𝑓(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури.

5. 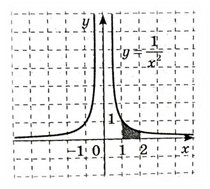      Обчисліть площу зафарбованої фігури, зображеної на малюнку.

6.       Матеріальна точка рухається прямолінійно зі швидкістю 𝑣(𝑡) = 4.5 − 𝑡 (час t вимірюється в секундах, швидкість v– у метрах на секунду).

Знайдіть шлях (у метрах), який точка пройшла за перші 6 с руху.

Завдання 7 передбачає встановлення відповідностей.До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ.

7.       Установіть відповідність між заданими функціями (1-4) та їхніми первісними (А-Д).

Розв’яжіть завдання 8 і 9( з короткою відповіддю). 

 Відповіді  запишіть  у бланку відповідей, дотримуючись правил запису.

8.       Знайдіть первісну для функції  𝑓𝑐𝑜𝑠 ^𝑥 − ¹ 𝑠𝑖𝑛 ^𝑥, графік якої

                                                                                                                                    3        2           2

проходить через точку А. У відповідь запишіть значення сталої с.

9.       Обчисліть: .

Наведіть повне розв’язання завдання 10.

Відповідь  та повне розв’язання запишіть у бланку відповідей.

10.   Обчисліть площу фігури, обмеженої лініями 𝑦 = 4 + 3𝑥 − 𝑥² і  𝑦 = 𝑥 − 4.

Варіант ІІ

У завданнях 1-6 мають по п’ять варіантів відповідей, серед яких тільки ОДИН  правильний. Виберіть  правильну, на вашу думку, відповідь та позначте її в бланку відповідей.

1. Знайдіть загальний вигляд первісної для функції 𝑓(𝑥) = 10𝑥⁹.

2.

3.

4. 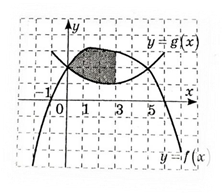      На рисунку зображено графіки функції 𝑦 = 𝑓(𝑥)  і 𝑦 = 𝑔(𝑥). Укажіть формулу для обчислення площі зафарбованої фігури.

5. 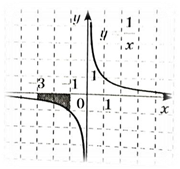      Обчисліть площу зафарбованої фігури, зображеної на малюнку.

6.       Матеріальна точка рухається прямолінійно зі швидкістю 𝑣(𝑡) = 2𝑡 − 1 (час t вимірюється в секундах, швидкість v– у метрах на секунду).

Знайдіть шлях (у метрах), який точка пройшла за перші 5 с руху.

Завдання 7 передбачає встановлення відповідностей.До кожного рядка, позначеного ЦИФРОЮ доберіть один рядок, позначений БУКВОЮ.

7.       Установіть відповідність між даними функціями (1-4) та їх первісними (А-Д):

Розв’яжіть завдання 8 і 9( з короткою відповіддю). 

 Відповіді  запишіть  у бланку відповідей, дотримуючись правил запису.

8.       Знайдіть первісну для функції  𝑓(𝑥) =𝑐𝑜𝑠 ^𝑥 + ¹ 𝑠𝑖𝑛 ^𝑥, графік якої проходить

                                                                                                                            2        2           2

𝜋 через точку А(; 1). У відповідь запишіть значення сталої с. 2

9.       Обчисліть:  .

Наведіть повне розв’язання завдання 10.

Відповідь  та повне розв’язання запишіть у бланку відповідей.

10.   Обчисліть площу фігури, обмеженої лініями 𝑦 = 4𝑥 − 𝑥² та 𝑦 = 4 – 𝑥.