Тригонометричні функції числового аргументу. Основні тригонометричні функції та тотожності.
Мета уроку: Закріпити вміння учнів застосувати основні співвідношення між тригонометричними функціями одного аргументу, поняття тригонометричних функцій числового аргументу.
Для того, щоб побачити всі зображення які містить конспект потрібно його завантажити!
Вчитель: Ніколенко Віра Василівна
Тема уроку: Тригонометричні функції числового аргументу. Основні тригонометричні функції та тотожності.
Мета уроку: Закріпити вміння учнів застосувати основні співвідношення між тригонометричними функціями одного аргументу, поняття тригонометричних функцій числового аргументу.
Обладнання: роздатковий матеріал, таблиці.
Тип уроку: комбінований.
Хід уроку
І. Організаційний момент
ІІ. Перевірка домашнього завдання
(відповідальні учні за перевірку домашнього завдання докладають про стан виконання. Відповіді до завдань записані на дошці).
ІІІ. Формування теми, мети і мотивація уроку.
На дошці таблиця – застосування тригонометричних функцій.
IV. Актуалізація опорних знань
- Розставити знаки тригонометричних функцій і пояснити їх походження (на дошці заздалегідь зображені кола)



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
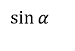
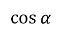
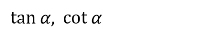
2) Заповнити пропуски (завдання записані на дошці заздалегідь)
А) ![]() + … = 1
+ … = 1
Б) … + ![]() =
= ![]()
В) ![]() =
= ![]()
![]() =
= ![]()
Г) ![]() = 1+ …
= 1+ …
Д) ![]() … = 1
… = 1
![]() 3) Заповнити таблицю (завдання записані на дошці заздалегідь)
3) Заповнити таблицю (завдання записані на дошці заздалегідь)
|
х |
|
|
|
|
|
|
х |
|
|
|
60 |
|
|
sin x |
|
|
|
|
|
|
cos x |
1 |
|
|
|
|
 №0 – мізинець – 0
№0 – мізинець – 0
№1 – безіменний – 30
№2 – середній – 45
№3- вказівний – 60
№4 – великий – 90
(Правило долоні – з малюнком – на таблиці)
-
Для sin
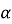 – номери пальців беруть від 0 до 4.
– номери пальців беруть від 0 до 4.
-
Для cos
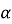 – від 4 до 0, наприклад
– від 4 до 0, наприклад
sin0 = ![]() = 0;
= 0;
cos30 = ![]() =
= ![]()
cos0 = ![]() = 1
= 1
cos90 = ![]() = 0 і т.д.
= 0 і т.д.
4) Клас в цей час працює над означеннями sin![]() , cos
, cos![]() , tg
, tg![]() , ctg
, ctg![]()
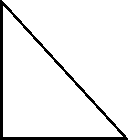 Встановити відповідність (дані на таблиці):
Встановити відповідність (дані на таблиці):
-
А) sin
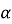 А)
А) 
![]()
![]() Б) cos
Б) cos![]() Б)
Б) ![]()
![]() B) tg
B) tg![]() B)
B) ![]()
![]()
![]()
![]() Г) ctg
Г) ctg![]() Г)
Г) ![]()
![]()
![]()
-

 А) sin
А) sin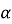 А)
А) 
![]()
![]() Б) cos
Б) cos![]() Б) x
Б) x
![]()
![]()
![]()
![]()
![]() B) tg
B) tg![]() B) y
B) y
![]() Г) ctg
Г) ctg![]() Г)
Г) ![]()
5) Перевірка знань учнів, що працювали біля дошки – фронтально.
V. Застосування знань, умінь і навичок.
1) Виконати №219 (стандарт)
Дано: sin![]() =
= ![]()
![]() <
< ![]() <
< ![]()
Знайти: cos![]() tg
tg![]() , ctg
, ctg![]()
- №142 (3) автор: Мерзляк
Довести тотожність:
![]() = 2tg2
= 2tg2![]()
- №141 (7) автор: Мерзляк
А) Спростити: (1+tg![]() )2 + (1-tg
)2 + (1-tg![]() )2
)2
Б) ![]() +
+ ![]()
4) tg![]() +
+ ![]()
5) №542 (2) академічний
Спростити: 5tg0 + 2sin(- ![]() ) – 3ctg (-
) – 3ctg (- ![]() ) +4cos (-
) +4cos (- ![]() )
)
Клас розв’язує разом з відповідаючи ми біля дошки. Перевірку проводимо фронтально.
6)Індивідуальна робота (по картках)
А) Спростити ![]()
Б) Довести тотожність (sin![]() + cos
+ cos ![]() )2 + (sin
)2 + (sin![]() – cos
– cos![]() )2=2
)2=2
В) Знайти найбільше і найменше значення
1- (cos2 – sin2![]() )
)
Індивідуальну роботу перевіряють консультанти і докладають вчителю в письмовій формі.
7) Усні вправи
А) Чи можуть одночасно виконувати рівності:
-
sin
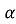 =
=  і cos
і cos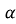 =
= 
-
tg
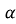 =
= 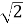 -1 і ctg
-1 і ctg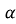 =
= 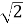 +1
+1
-
sin
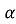 =
=  і cos
і cos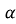 =
= 
Б) Знайти:
-
tg
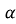 , якщо ctg
, якщо ctg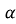 = 5
= 5
-
ctg
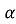 , якщо tg
, якщо tg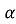 = -
= - 
VI. Лірична та інформаційна сторінка (виступають учні)
А) - Поняття синуса ввели індійські вчені, розглядаючи його, як половину хорди. Індійська назва синус означала, як половина тєтєви душ.
- Назва косинус і котангенс були введені в 1581 році
-
Значення sin
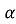 і cos
і cos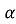 , такими, як ми користуємося сьогодні, були введені в трудах Еймра.
, такими, як ми користуємося сьогодні, були введені в трудах Еймра.
-
З поняттям tg
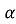 і ctg
і ctg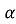 вчені зустрілися при розв’язуванні задач на обчислення тіні від стовпа.
вчені зустрілися при розв’язуванні задач на обчислення тіні від стовпа.
Б) Тригонометрична одиниця у віршах
- Пишем косинус в квадрате,
Пишем синуса квадрат
Их сложив, мы получаем
Единицу в аккурат!
cos2![]() + sin2
+ sin2![]() = 1
= 1
- Если тангенс на котангенс
Мы в задаче умнажаем
Непременно единицу
В результате получаем.
tg![]() *ctg
*ctg ![]() =1
=1
(читають діти)
VII. Самостійна робота (додаток 1, якщо залишиться час)
Бали в копілку оцінок учнів.
VIII. Підсумок уроку
IX. Домашнє завдання
- Повторити п.18-24 (академічний)
- №617 (6,7)
- №619, 623 (8,10)
- 627 (3), 625 (2,4)
Самостійна робота
Варіант 1
-
Спростіть вираз cos
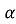 tg
tg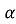
А. sin2![]() Б. cos
Б. cos![]() В.cos2
В.cos2![]() Г. sin
Г. sin![]()
2. Спростіть вираз sin2![]() +sin2
+sin2![]() -1
-1
А. 1 Б. 2 В. 0 Г. -1
3. Спростіть вираз tg2![]() (sin2
(sin2![]() -1)
-1)
A. –cos2![]() Б. –sin2
Б. –sin2![]() В. sin2
В. sin2![]() Г. cos2
Г. cos2![]()
4. Спростіть вираз 3sin250+30cos250 -2
А. 5 Б.4 В.-1 Г.1
5. Знайдіть cos![]() , якщо sin
, якщо sin![]() =
= ![]() і
і ![]() <
< ![]() <
< ![]()
А. 0,6 Б.-0,6 В. 1 Г. 0,8
Варіант 2
-
Спростіть вираз sin
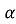 * ctg
* ctg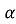
А. cos![]() Б. cos2
Б. cos2![]() В. sin
В. sin![]() Г. sin2
Г. sin2![]()
2. Спростіть вираз 1-sin2![]() -cos2
-cos2![]()
А. 1 Б. -1 В. Sin2![]() Г.0
Г.0
3. Спростіть вираз ctg2![]() (1-cos2
(1-cos2![]() )
)
А. –cos2![]() Б.sin2
Б.sin2![]() В. cos2
В. cos2![]() Г.-sin2
Г.-sin2![]()
4. Спростіть вираз -5cos212-15sin212-2
А. -3 Б.3 В. -7 Г.7
5. Знайдіть sin![]() , якщо cos
, якщо cos![]() =
=![]() I
I ![]() <
< ![]() <2
<2![]()
А. 0,8 Б.-0,8 В.1 Г. -0,6


про публікацію авторської розробки
Додати розробку

