Українські математики зображенні на монетах серії "Визначні особистості України"

Українські математики зображені на ювілейних монетах серії «Видатні особистості України»

За час існування Монетного двору Національного банку України випущено майже три сотні ювілейних і пам'ятних монет, об'єднаних у 23 тематичні серії, однією з найбільш визначних серед яких є серія «Видатні особистості України». Монети цієї серії присвячені видатним громадським діячам, ученим, митцям. Серед видатних особистостей є і представники математики – науки, яка за висловом славетного Карла Гауса, є царицею наук.  

1.      Перша така монета номіналом 2 грн була випущена у 2001 році – до 200-річчя з дня народження видатного математика Михайла Васильовича Остроградського (1801–1862).

 На аверсі монети в центрі зображено потік інтегральних кривих у прямокутній системі координат, малий Державний Герб України, написи в чотири рядки: УКРАЇНА, 2001, 2 ГРИВНІ та логотип Монетного двору Національного банку України. На реверсі монети зображено портрет М. В. Остроградського, ліворуч – інтеграл дробово-раціональної функції (метод інтегрування таких функцій названий його ім'ям), а праворуч – напис у два рядки півколом: 1801–1862, МИХАЙЛО ОСТРОГРАДСЬКИЙ.

М.В.Остроградський народився 24 вересня 1801 р. в селі Пашенівка Кобеляцького повіту на Полтавщині. Основні його наукові праці стосуються математичного аналізу, теоретичної механіки, математичної фізики, теорії ймовірностей. Крім того, він написав цілу низку чудових підручників з вищої та елементарної математики. М.В.Остроградський був членом п'яти академій – Паризької, С.-Петербурзької, Римської, Туринської та Американської.

Цікаво, але М.В.Остроградський так і не отримав російського вченого ступеня: 1820 року реакційно налаштована професура Харківського університету позбавила здібного юнака диплома про закінчення університету та атестата кандидата наук, мотивувавши своє рішення «вільнодумством» Остроградського й невідвідуванням ним лекцій з богослов'я. А всього через шість років знаменитий французький математик Коші писав про М.В.Остроградського: «Ця руська молода людина наділена великою проникливістю й вельми знаюча». Такої ж думки про нього були й інші вчителі Остроградського по паризькому Колеж де Франс, де після Харкова він продовжив вивчати математику: Лаплас, Фур'є, Ампер, Пуассон.  

2.      Ювілейна монета «Олександр Ляпунов» номіналом 2 грн випущена в 2007 році, виготовлена з нейзильберу і присвячена 150-річчю з дня народження видатного математика і механіка, академіка Петербурзької академії наук Олександра Михайловича Ляпунова (1857–1918), праці якого стосуються небесної механіки, математики, фізики й теорії ймовірностей.

На аверсі монети угорі розміщено малий Державний Герб України, під яким напис у два рядки – НАЦІОНАЛЬНИЙ БАНК УКРАЇНИ, геометричне зображення задачі з небесної механіки, а внизу – написи: 2 ГРИВНІ/2007 та логотип Монетного двору Національного банку України. На реверсі зображено портрет Олександра Ляпунова, а праворуч півколом розміщено написи: ОЛЕКСАНДР ЛЯПУНОВ/1857–1918.

Однією з найвизначніших праць О.М.Ляпунова стала його докторська дисертація «Загальна задача про стійкість руху», де всебічно розглянуто проблему стійкості руху систем з кінцевою кількістю ступенів свободи. Захист дисертації відбувся 30 вересня 1892 року в Московському університеті, а одним з опонентів виступив основоположник сучасної аеродинаміки професор М.Є.Жуковський, який свого часу продовжив дослідження з інтегрування рівнянь динаміки, розпочаті М.В.Остроградським.

3.      Ювілейна монета «Георгій Вороний» номіналом 2 грн випущена в 2008 році, виготовлена з нейзильберу і присвячена 140-річчю з дня народження одного з найвідоміших математиків світу Георгія Феодосійовича Вороного (1868–1908) – одного із творців геометрії чисел, засновника кількох нових напрямів у аналітичній теорії чисел і геометрії.

На аверсі монети стилізовано зображено діаграму Вороного, вгорі – малий Державний Герб України та розміщено написи: 2008 / 2 ГРИВНІ, ліворуч півколом – НАЦІОНАЛЬНИЙ БАНК УКРАЇНИ та логотип Монетного двору Національного банку України. На реверсі зображено портрет Георгія Вороного (ліворуч), праворуч – діаграму Вороного, роки життя 1868/1908 і внизу півколом напис – ГЕОРГІЙ ВОРОНИЙ.

Праці Георгія Вороного набули особливо великого значення в останні двадцять років. Це пов'язано з розвитком комп'ютерної графіки, молекулярної біології, радіаційної фізики, космології, створенням штучного інтелекту. За своє коротке (40 років) життя Г.Ф.Вороний написав усього 12 наукових робіт, але 8 з них успішно використовуються саме тепер майже в усіх країнах Європи, у США, Канаді, Японії, Австралії, Гонконгу, Новій Зеландії… Це – унікальне явище в математиці, де відкриття зазвичай вже через декілька років уважаються застарілими.

У Сеулі (Південна Корея) діє Дослідницький центр з діаграм Вороного, 2004 року в Токіо (Японія) були започатковані щорічні Міжнародні конференції з діаграм Вороного, а Інститут математики НАН України, починаючи з 1993 року, раз на п'ять років проводить міжнародні конференції, присвячені сучасному стану розвитку напрямів науки, закладених у працях Вороного.

4.      «Мико́ла Боголю́бов» — ювілейна монета номіналом 2 гривні, випущена Національним банком України2009 року. Присвячена 100-річчю від дня народження Миколи Боголюбова — одного із засновників сучасної фундаментальної науки, основоположника шкіл нелінійної механіки та статистичної фізики. Надзвичайний науковий талант Миколи Миколайовича дав змогу здійснити важливі для всієї світової науки відкриття в різних галузях. Його ім'я присвоєно Інституту теоретичної фізики Національної академії наук України.

На аверсі монети зображено графік та фрагменти формули з теорії нелінійних коливань та теоретичної фізики, на дзеркальному тлі вгорі розміщено малий Державний Герб України, напис півколом «НАЦІОНАЛЬНИЙ БАНК УКРАЇНИ» та логотип Монетного двору Національного банку України, унизу на матовому тлі — номінал «2 ГРИВНІ» (унизу), рік карбування монети «2009» (ліворуч).

На реверсі монети в центрі зображено портрет М. Боголюбова, на матовому тлі розміщено фрагмент формули, унизу на дзеркальному тлі розміщено напис півколом «МИКОЛА БОГОЛЮБОВ» та роки життя «1909» (ліворуч), «1992» (праворуч).

Основні праці Боголюбова з математики і механіки належать до варіаційного числення, наближених методів математичного аналізу, диференціальних рівнянь, рівнянь математичної фізики, асимптотичних методів нелінійної механіки і теорії динамічних систем. Перші публікації (1924–1928) присвячені проблемам варіаційного числення і теорії майже періодичних функцій. У наступні роки Боголюбов (разом зі своїм учителем М. М. Криловим розробив нові методи нелінійної механіки і загальної теорії динамічних систем. У циклі досліджень із проблем статистичної механіки (1939–1945) створив метод отримання кінетичних рівнянь, виходячи з механіки системи молекул.

У 1946 році Боголюбов уперше побудував мікроскопічну теорію надплинності, взявши за основу модель слабо ідеального бозе-газу. Через 10 років, виходячи з квантовомеханічної моделі електронного газу, який взаємодіє з іонною решіткою кристалу, узагальнивши свій апарат канонічних перетворень із теорії надплинності, створив мікроскопічну теорію надпровідності.

На початку 50-х років минулого століття Боголюбов звернувся до задач квантової теорії поля. Він створив перший варіант аксіоматичної побудови матриці розсіювання, який базується на оригінальній умові причинності (1954–1955). Запропонував математично коректний варіант теорії перенормувань, який використовує апарат узагальнених функцій Соболєва-Шварца, і ввів R-операцію (1955 р., разом з О. С. Парасюком). Розвинув регулярний метод покращення квантовопольових розв'язків, метод ренорм-групи (1955 р., разом з Д. В. Ширковим). Дав строге доведення дисперсійних співвідношень у теорії сильних взаємодій (1955–1956).

Боголюбову належить розробка методу систем зі спонтанно порушеною симетрією, який отримав назву методу квазісередніх (1960–1961). У середині 60-х років він звернувся до питань симетрії і динаміки кваркової моделі адронів. Увів представлення про нове квантове число «колір» (1965 р., разом із Струминським і Тавхелідзе).

Боголюбов є засновником радянських наукових шкіл у галузі нелінійної механіки, статистичної фізики і квантової теорії поля. Він був членом багатьох іноземних академій (у Болгарії, НДР, Польщі, США та ін.), наукових закладів і товариств.

Уміння Боголюбова виділяти загальні елементи у, здавалося б, найбільш різнорідних царинах фізики робить можливим плідне взаємне перенесення ідей і методів. Так, він одним з перших зрозумів до кінця глибоку математичну і фізичну спорідненість нерелятивістської задачі численних тіл і квантової теорії поля. Знаменитий американський фізик, керівник робіт зі створення першої атомної бомби Роберт Оппенгеймер у свій час був дуже здивований, коли вперше почув про праці Боголюбова у галузі дисперсійних співвідношень: він знав його праці щодо нелінійних коливань, тобто зовсім в іншій галузі. Зарубіжні вчені взагалі певний час мали припущення, що Боголюбов — це збірне ім'я, псевдонім, за яким заховано декілька фізиків і математиків. Тим не менше сам Боголюбов завжди вважав, що в його працях є щось спільне. Він казав: «Єднальною ланкою у мене була математика, бо мій підхід чи до проблем механіки, чи до проблем фізики — математичний». У сучасній науці вимагається відточена логіка математики, поєднана з інтуїцією фізика, що найвищою мірою було притаманне Боголюбову. Той же академік Логунов (тоді ректор Московського університету) ставив Боголюбова в один ряд з такими корифеями науки, як Павлов і Вернадський, не тільки за рівнем його наукових досягнень, але й у моральному плані: «Звичайно, в одному ряду вони стоять передусім завдяки нечуваному обдарованню, але кожний водночас є зразком найвищих моральних якостей. Немає жодних сумнівів, що коли наше наукове середовище втратить цей моральний капітал, таку втрату не заповнить жодне наймудріше планування досліджень».

5.      Миха́йло Кравчу́к — ювілейна монета номіналом 2 гривні, випущена Національним банком України 2012 року. Присвячена математику, педагогу і громадському діячеві Михайлу Пилиповичу Кравчуку — академіку Академії наук України, автору фундаментальних праць з алгебри, математичного аналізу, теорії лінійних перетворень, теорій функцій тощо. Завдяки широкому колу наукових інтересів і результатам досліджень Михайло Кравчук став відомим не лише в Україні, а й поза її межами.

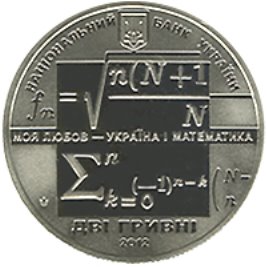
На аверсі монети розміщено: малий Державний Герб України та напис півколом «НАЦІОНАЛЬНИЙ БАНК УКРАЇНИ», фрагмент формули М. П. Кравчука, посередині — вислів ученого «МОЯ ЛЮБОВ» — «УКРАЇНА І МАТЕМАТИКА», унизу номінал — «ДВІ ГРИВНІ», рік карбування монети — «2012» та логотип Монетного двору Національного банку України.

На реверсі монети на тлі цифр, що уособлюють сферу діяльності математика, зображено портрет та написи: «МИХАЙЛО/КРАВЧУК», роки життя «1892/1942» (праворуч).

Відомо, що Джон Вінсент Атанасов при створенні першого комп'ютера користувався з наукового доробку Кравчука. Про це випадково дізнався бібліограф українського вченого д-р Іван Качановський з Вашингтона.

«Я знайшов листа американського вченого до М. Кравчука, де він пише, що користався його матеріалом», — згадує д-р І. Качановський. Тільки в 2001 р. праці Кравчука були використані в Америці у 15 наукових статтях.

Михайло Кравчук — один з засновників ЕОМ (електронно-обчислювальної машини). Його розробки американці та японці застосували на телебаченні. Його учень, конструктор Сергій Корольов став усесвітньовідомим ученим. Уже в 21 сторіччі ЮНЕСКО внесла ім'я Михайла Кравчука до переліку найвизначніших осіб.

Михайло Кравчук не обмежувався дослідницькою роботою. Йому належить велика роль у розвитку математичної освіти як на рівні середньої, так і вищої школи, у розробці української математичної термінології, в організації наукового життя в добу першого пореволюційного відродження в Україні. Він відомий ще й тим, що першим в Україні почав писати математичні праці українською мовою, за що був оголошений «націоналістом» і запроторений до більшовицьких концтаборів.

Розділи теоретичної і прикладної математики, у яких знайшли своє застосування здобутки Кравчука:

Випадкові блукання. Симетричні матриці Кравчука та біноміальні сподівання.

Мартингали. Поліноми Кравчука і мультиноміальні розподіли.

Алгебри Лі та поліноми Кравчука.

Групи Лі. Відбиття. Матриці Кравчука та групові елементи.

Квантова ймовірність та тензорна алгебра. Матриці Кравчука як власні вектори.

Коефіцієнти Клебша-Гордана та поліноми Кравчука.

Перетворення Кравчука.

Поліноми Кравчука як гіпергеометричні функції.

Гаусові квадратури. Нулі поліномів Кравчука. Сумація Гаусса-Кравчука.

Теорія кодування.

Упродовж останніх років з'явилися несподівані, на перший погляд, застосування наукових здобутків Кравчука в прикладній математиці та комп'ютерних науках. Географія відповідних досліджень дуже широка. Обмежимося лише кількома прикладами.

Так, у 2003 році науковці електроінженерного факультету Університету Малайї (Куала-Лумпур, Малайзія) запропонували новий метод обробки та реконструкції зображень за допомогою моментів Кравчука. На ряді експериментів із відновлення образів об'єктів вони підтвердили суттєві переваги використання інваріантів моментів Кравчука як в умовах відсутності, так і за присутності шумів. На ІІІ Міжнародному симпозіумі з 3-вимірної обробки даних, візуалізації та передачі інформації (The Third International Symposium on 3D Data Processing, Visualization, and Transmission) у 2006 році група грецьких учених доповіла про 3-вимірні пошукові алгоритми, що базуються на тривимірних моментах Кравчука, і мають на меті здійснення обробки тривимірних зображень.

У 2009 році на Міжнародній спільній конференції з нейронних мереж (Атланта, Джорджія, США) групою французьких, американських та німецьких вчених була зроблена доповідь, в якій, зокрема, було показано ефективність застосування зважених 3-вимірних моментів Кравчука як засобу аналізу даних для розпізнавання характеру пухлин.

У 2009 році у видавництві Шпрінгер вийшла книга «Advances in Neural Networks» (Досягнення в теорії нейронних мереж) з підсумками 6-го Міжнародного симпозіуму з нейронних мереж, що проходив у Китаї. Один із розділів під назвою «Image Analysis by Modified Krawtchouk Moments» (Аналіз зображень за допомогою моментів Кравчука) написаний групою китайських науковців.

У виданні «International Journal of Computer Science and Network Security», VOL.9 No.1, January 2009 (Міжнародний журнал з комп'ютерних наук та безпеки мереж) вміщено статтю під назвою «Krawtchouk Moment Feature Extraction for Neural Arabic Handwritten Words Recognition» (Виділення ознак моментами Кравчука з метою нейронного розпізнавання арабських рукописних слів), яку написали марокканські фахівці. Цікаво, що в переліку посилань знаходимо статтю Кравчука 1929 року, опубліковану в працях Сільськогосподарського інституту.

Уже згаданий вище Філіп Феінсілвер з університету Південного Іллінойсу та Рене Шотт (René Schott) з університету Анрі Пуанкаре-Нансі I у своїй праці 2009 року «On Krawtchouk Transforms» (Про перетворення Кравчука) досліджують питання, пов'язані із застосуванням перетворень Кравчука в теорії кодування. Виявляється, активне використання поліномів та перетворення Кравчука для потреб цієї теорії розпочалося ще в 70-х роках минулого століття (теореми Дельсарта та Мас Вілльямса)

Дуже хочеться сподіватися, що ще не одному представникові «цариці наук» буде присвячено вітчизняні монети, які нагадуватимуть нам слова американського філософа Д.Сантаяни (1863–1952): «Подібно до того як всі мистецтва пориваються до музики, так науки прагнуть до математики».