Уписані і центральні кути

Тема. Уписані і центральні кути^[*]

Мета: учні мають засвоїти поняття: центральний кут, дуга (як частина кола), дуга, що відповідає даному центрально­му куту, кутова міра дуги, кут, уписаний в коло і дуга, на яку спирається вписаний кут; а також засвоїти теорему про міру вписаного кута і схему її доведення. Виробити первинні вміння учнів відтворювати вивчені поняття, розрізняти на готовому рисунку вивчені об'єкти і ви­конувати їх зображення за словесним описом, а також застосовувати вивчену властивість для розв'язування базових задач.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 21 «Центральні і вписані кути (кути в колі)», набір паперових моделей кутів та кола.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання    

Оскільки домашнє завдання містить задачі, подібні до розв'язаних в класі, письмову частину домашнього завдання перевіряємо, зібравши зошити учнів на перевірку.

Засвоєння теоретичного матеріалу можна перевірити під час теоретичного опитування (яке можна провести у формі теоретичної самостійної роботи).

Самостійна   робота   №   8

1. Продовжимо всі радіуси кола на одну й ту саму довжину (в напрямку від центра). Яку лінію утворять їх кінці?
2. На колі взято точку. Скільки діаметрів і скільки хорд можна провести через цю точку?
3. Чи може хорда бути втричі більша за радіус того самого кола?
4. Всередині трикутника взяли точку, рівновіддалену від його вершин. Чим є ця точка для даного трикутника? Що представляє собою відстань від вибраної точки до вершин трикутника?
5. Всередині трикутника взяли точку, рівновіддалену від сторін цього трикутника. Чим є ця точка для цього трикутника? Що представляє собою відстань від вибраної точки до сторін трикутника?
6. На луки вивели пастися козу, прив'язавши її до кілка мотузкою, довжина якої 5 м. Яку форму матиме ділянка, на якій тварина зможе щипати траву?

(Відповіді: 1. Лінію кола, концентричного з даним, радіус якого дорівнює сумі радіуса даного кола і довжини відрізка. 2. Діаметр один; хорд — безліч. 3. Ні, бо найбільша хорда — це діаметр, а діаметр удвічі більший за радіус. 4. Точка є центром описаного кола, відстань — його радіусом. 5. Точка є центром уписаного кола, відстань — його радіусом. 6. Круг радіусом 5 м з центром в місці закріплення кілка.)

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Для усвідомлення учнями логіки викладання матеріалу і залучення учнів до цілевизначення на уроці можна запропо­нувати учням виконати роботу зі схемою № 7.

Схема № 7

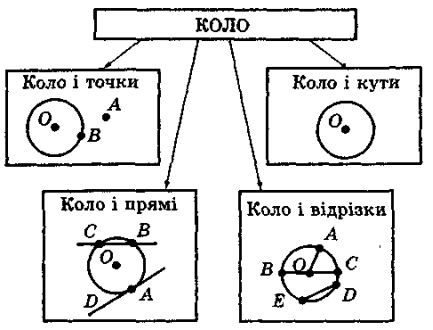
Далі формулюється основна дидактична мета уроку — ви­вчення можливих варіантів взаємного розміщення кола і кута.

IV. Актуалізація опорних знань і вмінь учнів

Можна організувати самостійну роботу учнів з повторення змісту базових понять: коло та його елементи, кут, вимірювання кутів, рівнобедрений трикутник, зовнішній кут трикутника.

V. Засвоєння нових знань    

План вивчення матеріалу

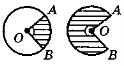
1. Можливі варіанти взаємного розміщення кута і кола.
2. Поняття дуги кола. Вимірювання дуг кола.
3. Центральний кут, вимірювання центральних кутів.
4. Уписаний   кут,   вимірювання   вписаних   кутів   (теоре­ма 13).

Методичний коментар

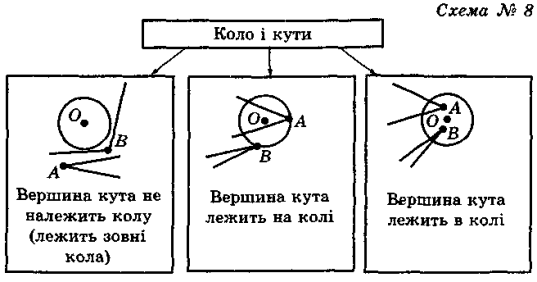
Відповідно до п. 3 уроку є доцільним розпочати вивчення нового матеріалу з розгляду можливих варіантів розміщення кута відносно кола (схема № 8). Виокремити два варіанти, які вивчатимуться на уроці (в обох випадках вершина кута суміщається з точкою кола або центром кола, а сторони кута перетинають коло). Далі перейти до частин кола та їх вимірю­вання. (Слід зауважити, що вимірювання дуг кола в градусах дає змогу встановити градусну міру всього кола — можна запропонувати учням довести цей факт самостійно.) Сфор­мулювати конструктивні означення центрального кута і впи­саного кута, ввести поняття про дуги, що відповідають цим кутам; вивчити питання про вимірювання цих кутів через відповідні дуги кола. Далі, відповідно до тексту підручника, довести теорему 13.

Формуванню знань сприятиме використання таблиці № 21.

Таблиця № 21

Центральні та вписані кути

VI. Первинне усвідомлення матеріалу   

Усні   вправи

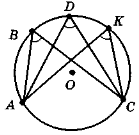
1. На рис. 125 знайдіть і назвіть центральні кути, вписані кути та відповідні їм дуги кола.

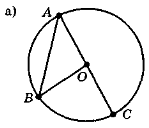
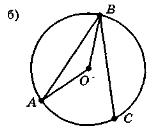
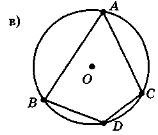
Рис. 125

2. Знайдіть градусні міри центрального і вписаного кутів, якщо:

а) відповідна дуга дорівнює  60°;

б) відповідна дуга дорівнює третині кола;

в) уписаний кут на 50°  менший від центрального кута, що спирається на ту саму дугу.

Письмові   вправи

Знайдіть градусну міру центрального кута, який спирається на дугу, що становить частину кола.

VІІ. Підсумки уроку

Запитання   до   класу

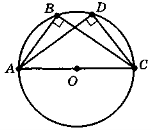
Чи все правильно на рис. 126?

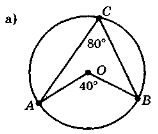
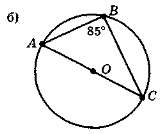
Рис. 126

VIII. Домашнє завдання

1. Вивчити означення (див. конспект) теореми 13.
2. Розв'язати задачі.

1) Знайдіть градусну міру вписаного кута, який спирається на дугу, що доповнює дугу в 150°  до повного кола.

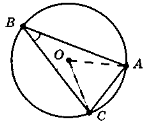
2) Через точку А кола проведено дві хорди АВ і АС. Знай­діть кут АОВ, якщо кут між хордами дорівнює 40°; 90°; а градусів.

3. На повторення: № 551.

^[*] Матеріал подається як додатковий.