Урок (наукова конференція) на тему: "Інтеграл та його застосування"

Про матеріал

Дидактичний матеріал до нестандартного уроку (урок - наукова конференція) на тему "Інтеграл та його застосування".

Перегляд файлу

Мета:

Навчальна: поглибити й розширити знання учнів про інтеграл; відпрацювати навички знаходження інтегралів та їх застосування до розв’язування задач.

Розвиваюча: розвивати навики самостійного мислення,інтелектуальні навики(аналіз,синтез,порівняння,співставлення),увагу,пам’ять.

Виховна: виховувати вміння раціонально використовувати робочий час, акуратність, наполегливість, інтерес до вивчення математики. Тип уроку: узагальнення і систематизація навчального матеріалу.

Вид уроку: Наукова конференція.

Конструктор уроку: І. Організаційна частина.

ІІ. Перевірка домашнього завдання.

• Дослідницька робота.

ІІІ. Актуалізація знань, умінь і навичок.

• Термінологічний диктант («Теоретичний марафон»).

IV. Повідомлення теми, мети і плану уроку. Мотивація навчальної діяльності учнів.

• «Самооцінка».

• «Шкала впевненості» (рефлексія учнів на початку уроку)

V. Узагальнення і систематизація матеріалу.

• Групова робота «Теоретиків»;

• групова робота «Практиків»;

• групова робота «Фізиків»;

• групова робота «Економістів»;

• дидактична гра «Вершина знань» (командна робота);

• картки – завдання;  опорний конспект.

VІ. Підведення підсумків. Рефлексія.

• «Сніжна грудка»;

• «Шкала впевненості» (рефлексія учнів наприкінці уроку)

VІІ. Домашнє завдання.

• Обов’язковий мінімум;  тренувальні завдання;  творчі завдання.

Термінологічний диктант

«Теоретичний марафон»

(актуалізація) Початковий рівень

(за кожну правильну відповідь – 0,5 бали)

Гетерогенні групи теоретиків, практиків, фізиків, економістів отримуєте текст, в який потрібно вписати пропущені слова, а потім здійснити взаємоперевірку між групами з подальшим зачитуванням правильних відповідей.

Формула Ньютона – Лейбніца _f xdx..., де Fx...? a

1. Задачі, у яких використовуються математичні поняття, називають …

2. Рівняння ^x2^y2R задає … із центром … , де R - …

3. Пряма, паралельна осі Ох, задається рівнянням у...

4. Шлях, пройдений тілом за інтервал часу^_^t1;^t2^_, виражається через



інтеграл так: s... 5. Роботу змінної сили F^_x^_ під час переміщення тіла із точки а в точку b

 

можна знайти за формулоFxю А...

 

6. Електричний заряд, що проходить через поперечний переріз провідника за проміжок часу від ^t₁ до ^t₂ , можна знайти за формулою q...

«Самооцінка» (мотивація)

- Хто сьогодні готовий отримати найвищу оцінку?

- Хто добре готовий до уроку?

- Хто не готовий?

«Шкала впевненості» (рефлексія учнів на початку уроку)

Результати роботи – 100 – бальна шкала:

Оцінити власне почуття впевненості у знаннях 100-бальною шкалою.

*1 -*	*10 -*	*20 -*	*30 -*	*40 -*	*50 -*	*60 -*	*70 -*	*80 -*	*90 -*	*100 -*
*Зовсім не впевнений*							*Абсолютно впевнений*

Повідомлення групи «теоретиків»

(удосконалення вмінь і навичок)

Середній рівень (3 бали)

Об’єми тіл

V^b_Sxdx

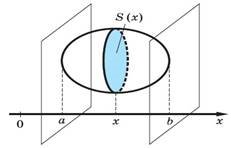
Якщо тіло вміщене між двома перпендикулярними до осі Ох площинами, що проходять через точки х = а і x = b, то ,

де S (x) — площа перерізу тіла площиною, що проходить через точку х [a; b] і перпендикулярна доосі Ох.

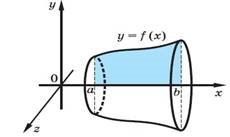
Якщо тіло одержане в результаті обертання навколо осі Ох

криволінійної трапеції, яка обмежена

графіком неперервної і невід’ємної на відрізку [a; b] функції у = f (x) і прямими х = а і x = b, то

V _f ²xdx

Повідомлення групи «практиків»

(удосконалення вмінь і навичок)

Достатній рівень (3 бали)

1. Об’єм кулі

2. Об’єм циліндра

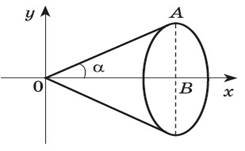
3. Об’єм конуса

x2  y2  R2,

y² R² x². Якщо y  0, то y  R²x².

V _R² x²dx 

R

 x3

R²x  3 ^ _R 43



V  ⁴R³

к. 3



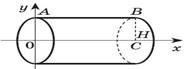
Циліндр – це тіло, отримане обертанням прямокутника ОАВС навколо осі Ох.

Складемо рівняння твірної циліндра АВ. yR.

V R²dxR²x₀^HR²H

Таким чином,

Трикутник ОАВ обертається навколо осі Ох. Складемо

рівняння твірної конуса ОА:

ykx, де k _tg__^R. H

H 2 2 x2 ^H1

 R  R

V ^_H x_dx  H2  3 0  3

V ¹R²Н кoн. 3

V R²Н

ц.

Повідомлення групи «фізиків»

(удосконалення вмінь і навичок)

Високий рівень (3 бали)

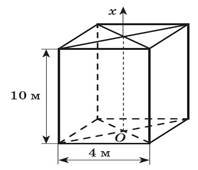
Прикладна задача. Робота сили F^_x^_ під час переміщення тіла із точки а в

 

точку b дорівнює A^Fxdx. Обчисліть роботу, яку треба виконати для a

викачування води з ями завглибшки 10 м, яка має квадратний переріз зі стороною 4 м. Густина води 10³кг/м³.

Розв’язання:

Повідомлення групи «економістів»

(удосконалення вмінь і навичок) Високий рівень (3 бали)

Прикладна задача. Продуктивність праці робітника приблизно виражається формулою f ^_t^_0,0033t²0,089t20,96, де t робочий час (у годинах).

 

Обчисліть обсяг продукції, випущеної протягом місяця, вважаючи, що робочий день триває 8 годин, а на місяць припадає 22 робочі дні. Розв’язання:

Дидактична гра «Вершина знань» (командна робота)

Розщілина «Графічна»

Середній рівень (3 бали)

Знайти первісну функцій, що задовольняють дану умову:

1 x

1) f (x)  sin  4cos4x, F()  3;

3 3

2) f (x)  ³x² ₃⁴_x, F(1)0; 3) f (x)  _2x⁸_₁, F(0,5)  7 .

Розв’язання:

Гірський хребет «Інтеграла»

Достатній рівень (3 бали)

Обчислити інтеграли:

1) (x1)(x1)(x2)dx;



4 1 2x1 5x1

 

2) cos4x 4dx ; 3) 0 10x dx.

Розв’язання:

Плато «Криволінійна трапеція»

Достатній рівень (3 бали)

Обчислити площу фігури, обмеженої лініями:

1) ycosx, x=0, x= та віссю абсцис;

2) y 4x , y=0, x=5; 3) y , x+y=6. x

Розв’язання:

Вершина «Об’ємного успіху»

Високий рівень (3 бали)

Знайти об’єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої:

1. графіком функції y=4x та прямими х=9, у=0;



2. косинусоїдою y=cos x та прямими х=9, x , у=0;

3. прямими у=2х, х=0, у=5.

Розв’язання:

Підсумки уроку «Сніжна грудка»

Початковий рівень

«Шкала впевненості» (рефлексія учнів наприкінці уроку)

Результати роботи – 100 – бальна шкала:

1. Порівняти очікування з результатом 100-бальною шкалою.

2. Що сприяло успіху?

3. Що заважало?

4. В чому причина невдач?

*1 -*	*10 -*	*20 -*	*30 -*	*40 -*	*50 -*	*60 -*	*70 -*	*80 -*	*90 -*	*100 -*
*Зовсім не впевнений*							*Абсолютно впевнений*

Домашнє завдання (диференційоване)

Домашня дослідницька робота:

Дослідити чи можна обчислити визначений інтеграл за допомогою підстановки

Щоб обчислити визначений інтеграл, застосовують підстановку. Але в цьому разі є одна особливість, на яку треба звернути увагу.

Як з’ясувалось метод підстановки полягає в тому, що для зведення заданого невизначеного інтеграла до табличного аргумент подають через нову змінну; потім знаходять невизначений інтеграл і результат подають через початкову змінну (аргумент). У випадку ж визначеного інтеграла немає потреби повертатися до початково заданої змінної.

Розглянемо приклад. Знайти ^0 ₍₁_^xdx_x2₎3 .

Розв’язання.

Покладемо 1x² z; тоді 2xdxdz, звідки xdx_^dz.

Оскільки введена нова змінна, зв’язана з попередньою рівністю 1x² z, то межі зміни змінної z, тобто межі інтегрування за змінною z, будуть вже іншими.

Їх можна знайти з рівності 1x² z, змінюючи аргумент х його значеннями 0 і .