Урок №2 "Логарифм і його властивості"

Урок №2

Тема уроку. Логарифми та їх властивості.

Мета уроку. Вивчення основних властивостей логарифмів, формувати уміння умінь обчислення виразів із логарифмами; розвивати наполегливість, самостійність, пам'ять, увагу логічне мислення, пізнавальну активність; виховувати інтерес до предмету математики.

Тип уроку:: формування знань, вироблення вмінь.

Хід уроку

І. Перевірка домашнього завдання.

1. Три учні відтворюють розв'язування вправ № 19.3, 19.10, 19.12.

2. Усне розв'язування вправ на обчислення логарифмів з вико­ристанням таблиці  для усних обчислень.

Таблиця

3. Відповіді на запитання, що виникли в учнів під час виконання домашнього завдання.

II. Сприймання і усвідомлення основних властивостей логарифмів.

При виконанні перетворень виразів, які містять логарифми, при обчисленнях і при розв'язуванні рівнянь, нерівностей часто використовуються властивості логарифмів.

Для будь-яких а > 0, а ≠ 1 і будь-яких додатних х і у виконуються рівності:

Доведемо рівності 3—7. За основною логарифмічною тотожністю

                         (І)

                       (II)

Перемноживши рівності (І) і (II), одержуємо:

 ху = · = ,  

звідси за означенням логарифма маємо

log_a xy = log_a x + log_a y.

Отже, логарифм добутку дорівнює сумі логарифмів.

Розділивши рівності (І) і (II), одержуємо: = ,

звідси за означенням логарифма маємо: log_a = log_a х – log_a у.

Отже, логарифм частки дорівнює різниці логарифмів.

Піднісши ліву і праву частини рівності (І) до степеня з показ­ником р, маємо:                             (ІІІ)

звідси за означенням логарифма маємо: log_а х ^р = p log_а x.

Отже, логарифм степеня дорівнює добутку показника сте­пеня на логарифм основи цього степеня.

З рівності (III) маємо: , звідси за означенням логарифма маємо:

, тоді p;  .

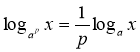Формула 7 називається формулою переходу від одної основи логарифма до другої основи. Доведемо її.

За правилом логарифмування степеня (формула 5) та основ­ною логарифмічною тотожністю одержуємо:

,

звідси                log_b х = log_a х · log_b a

або                     log_a = .

За допомогою формули 7 можна знаходити логарифми з довіль­ною основою а, маючи таблиці логарифмів, складених для якої-небудь основи b. Найбільш вживаними є таблиці десяткових і на­туральних логарифмів.

III. Осмислення основних властивостей логарифмів.

Розглянемо приклади використання формул 3-7. Обчислимо:

1) log₆ 18 + log₆ 2 = log₆(18 – 2) = log₆ 36 = 2;

2) log₁₂ 48 – log₁₂ 4 = log₆ = log₁₂ 12 = 1;

3) log₆ = log₆ = log₆ 3 = · 1 = ;

4) log₁₂₅ 5 = log₁₂₅ 5 = log₅ 5 = · 1 = ;

5) = log₄ 16 = log₄ 4² = 2 log₄ 4 = 2 · 1 = 2.

3. Виконання вправ № 19.13, 19.15,19.21.

«На замітку абітурієнту»

В цій рубриці представленні завдання, які були на ЗНО попередніх років:

Обчисліть

Правильна відповідь: 2 (вказівка: за властивістю логарифма)

ІV. Самостійна робота, навчального характеру (5 хвилин)

Варіант 1.

Знайдіть значення виразу:

Варіант 2.

Знайдіть значення виразу:

.

V. Підведення підсумків уроку.

Продовжіть властивості логарифмів.

1. Чому дорівнює логарифм добутку?
2. Чому дорівнює логарифм частки?
3. Чому дорівнює логарифм степеня?
4. Запишіть  формулу переходу від однієї основи логарифма до іншої.

VI. Домашнє завдання.

1. Опрацювати п.19, ст.181( А.Г.Мерзляк). Вивчити властивості логарифмів.
2. Виконати вправи: № 19.14, 19.16,19.22,19.24 - письмово.