Урок з алгебри та початків аналізу в 11 класі на тему "Правила обчислення похідних"

Тема уроку: Правила обчислення похідних

Мета уроку:  закріпити знання учнів про похідні елементарних функцій, про правила обчислення похідних суми та добутку функцій, сформулювати теорему про похідну частки функцій, сформувати вміння знаходити  похідну частки, застосовувати правила обчислення похідних до розв’язування вправ та задач;

- розвивати пам'ять, увагу, логічне мислення, культуру математичних записів;

- виховувати  почуття  відповідальності , впевненість у власних силах, інтерес до математики

Тип уроку: комбінований

Обладнання: підручник, комп’ютер, презентація, картки  з завданнями,                         картки самооцінювання, додаток - відомості про вчених-математиків

Епіграф:   Хто хоче обмежитися теперішнім, має знати: без знання минулого, не     зрозуміє його.   ( Піфагор )                     

                                       Хід уроку

І. Організаційний етап.  Перевірка домашнього завдання.
№ 8.2, 8.4
- Консультанти повідомляють про наявність і правильність виконання домашнього завдання.

-Роздати листки само оцінювання. Нагадати правила роботи на уроці

ІІ. Повідомлення теми, мети уроку        

Сьогодні  у нас відкритий урок на якому присутні гості, тому будьте уважні та зосереджені, вкінці уроку побачимо чи досягнули поставленої мети . Епіграфом сьогоднішнього уроку я вибрала слова славетного математика Піфагора… (учні записують дату і тему уроку)

ІІІ. Актуалізація опорних знань.     

  Бліц-опитування

1.Сформулюйте означення похідної функції в даній точці.
2.В чому полягає геометричний зміст похідної?
3.В чому полягає фізичний зміст похідної?
4. Як знайти кутовий коефіцієнт дотичної до графіка функції в заданій точці?

 5. Знайдіть похідні функцій…. а)  в точці ;    б)  в точці ;
 

в)  в точці ;    г)  в точці .
 

Відповідь: а) 0;    б) ;    в) 0,5 ;    г) -1.

   6. Сформулюйте теорему про похідну суми двох функцій.

   7.Сформулюйте теорему про похідну різниці двох функцій.

      8.Сформулюйте теорему про похідну добутку двох функцій.

ІV. Мотиваційний етап уроку.

Ви вже вмієте обчислювати похідні суми, різниці та добутку функцій. Сьогодні на уроці навчимося обчислювати похідну частки двох функцій. Зараз послухайте про видатного математика, який зробив великий внесок у дослідженні даної теми.

 Михайло Васильович Остроградський народився 12 вересня 1801 р. в с. Пашенному Кобиляцького повіту Полтавської губернії. Культурна родина, працьовитий народ, широкі лани і зелені гаї— ось у таких умовах минули дитячі роки майбутнього вченого. Малого Михайлика цікавило все: як запрягають коней і орють землю, як працюють вітряк і водяний млин. Особливо цікавило його те, що можна було вимірювати. Він завжди носив із собою мотузку і вимірював глибину колодязів, розміри будівель, величину земельних ділянок.

За свою майже 40-річну наукову діяльність Михайло Васильович написав понад 50 наукових праць з різних галузей математики: математичного аналізу, аналітичної і небесної механіки, математичної фізики, балістики тощо.

У 1837 р. Остроградський видав лекції, які він читав у Морському кадетському корпусі, під назвою: "Лекції з алгебраїчного і трансцендентного аналізу". Це був один з перших і досконалих посібників для студентів вищих шкіл.

Остроградський був енергійним проповідником прогресивних педагогічних ідей. Зокрема, він рекомендував у навчальному процесі додержувати таких вимог: збуджувати в учнів інтерес; добиватися свідомого засвоєння; розвивати самостійне мислення; вести точний науковий виклад; застосовувати наочність; проводити практичні роботи. Остроградський вказував, що навчання повинно бути реальним, близьким до життя. Він писав, що вчителі повинні любити свою справу, бо в хороших учителів будуть хороші учні. Свої педагогічні погляди М. В. Остроградський виклав у підручниках з елементарної і вищої математики.

За світоглядом і переконаннями Остроградський був матеріалістом і атеїстом. Він палко любив свій край, свій народ, свою культуру. Улюбленим його письменником був Т. Г. Шевченко, значну частину творів якого Остроградський знав напам'ять і охоче декламував. З такою самою щирою повагою і любов'ю ставився до Остроградського і Великий Кобзар. Шевченко приїздив до Остроградського у 1858 р.

V. Вивчення нового матеріалу

П.8 на с. 71 у підручнику

Теорема про похідну частки функцій    Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і g(x), то функція  диференційована в цій точці і .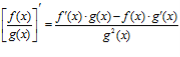
 

Доведення     Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Нехай , тоді f(x)=у(х). Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, . Виразимо з цієї формули 
 

 і підставимо замість у(х) значення , тоді будемо мати:
 

.

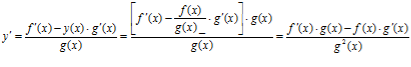Отже,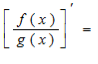 

Приклад: Знайдіть похідні функцій
 

а) 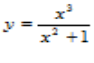                         б)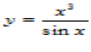    
 

Розв’язання
 

а)    .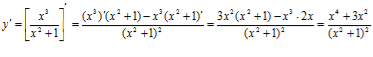
 

б)    .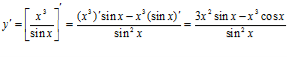

VІ. Формування вмінь та навичок учнів

Виконання вправ (слайд       ) 

1. Знайдіть похідну функцій:

а)    ;        б)    ;
 

в)    ;    г)    .
 

Відповідь:    а)    6х-5;        б)    ;
 

в)    ;            г)    .

2. Знайдіть похідні ф-цій:

а)    ;            б)    ;

в)    ;                г)    .
Відповідь :

Відповідь:    а)    ;        б)    ;
 

в)    ;    г)    .
3. Задача № 1  (відповідь 20 м/с)

(Учні – експерти з груп розповідають цікаві відомості про вчених Лейбніца та Ньютона)  додаток 1

Сильніші учні отримують картки із завданнями, які розв’язують з поясненням біля дошки: дано функції f(х) та g(х)

1. знайди суму похідних ф-цій
2. знайди різницю похідних ф-цій
3. знайди похідну добутку ф-цій
4. знайди похідну частки ф-цій

Решта класу виконує вправу № 8.5, 8.7 з підручника

VІІ. Підсумок уроку.
- Рефлексія  (Учні підраховують свої бали, ставлять смайлик настрою)

Запитання до класу:

1. Чи сподобався урок?
2. Що запам'яталося найбільше? Чи досягнуто поставленої мети?
3. Над чим ще потрібно працювати?  Як оцінюєте власну роботу на уроці?

-Оцінювання учнів
VІІІ. Домашнє завдання : п 8, № 8.6, 8.8