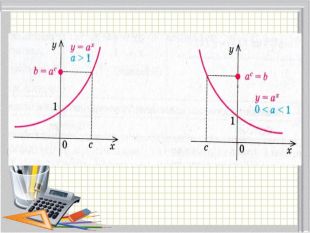
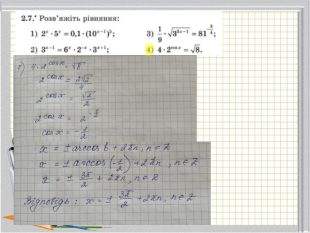
Урок №4 Розв’язування показникових рівнянь
Про матеріал
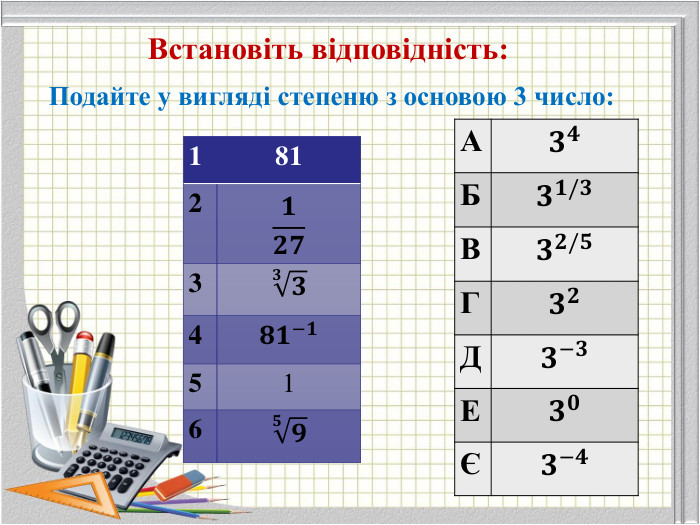
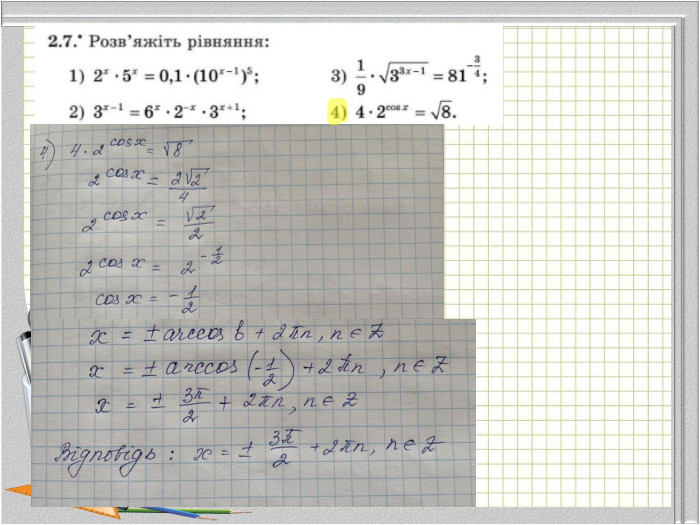
В презнтації наведені приклади розв'язання рівнянь з підручника:
Мерзляк А. Г. Математика : алгебра і початки аналізу та геометрія, рівень стандарту : підруч. для 11 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський та ін. — Х. : Гімназія, 2019. — 208 с. : іл. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку