Урок алгебри в 9 класі "Статистичні дані. Способи подання даних та їх обробка""

Жушман Марина Миколаївна

Криворізька загальноосвітня школа І-ІІІ ступенів № 63

План-конспект уроку алгебри в 9 класі

Тема уроку. Статистичні дані. Способи подання даних та їх обробка

Формування компетентностей:

• предметна компетентність: розглянути поняття статистики як науки; сформувати уявлення про предмет вивчення математичної статистики. Працювати над усвідомленим розумінням змісту понять: вибірка; варіаційний ряд; частота вибірки, відносна частота вибірки; частотна таблиця та гістограма, центральні тенденції вибірки (середнє значення, мода, медіана). Навчати учнів наводити приклади статистичних даних у вигляді таблиць та гістограм; розв’язувати задачі, що передбачають подання статистичних даних у вигляді таблиць та гістограм та знаходити центральні тенденції вибірки.
• Ключові компетентності:

• математична компетентність – формувати вміння будувати і досліджувати найпростіші математичні моделі реальних процесів, інтерпретувати та оцінювати результати;
• уміння вчитися впродовж життя – сприяти усвідомленню цінності нових знань і вмінь, зацікавленості у пізнанні нового;
• ініціативність і підприємливість – формування вміння робити висновки та приймати оптимальні рішення на основі інформації, поданої в різних формах, зокрема в таблицях, діаграмах;
• соціальна та громадянська компетентність – сприяти самовихованню свідомого ставлення до навчання, скрупульозності, акуратності.

Тип уроку: засвоєння нових знань та вмінь

Обладнання: опорні конспекти, картки з завданнями, ноутбук, мультимедійна дошка, проектор.

Хід уроку

I. Організаційний момент (Слайд 1)

Дорогі учні, шановні гості! Рада вітати вас на сьогоднішньому уроці, який, я сподіваюсь, буде цікавим і підтвердить слова про те, що математика безмежно різноманітна і міститься у всьому.

Звертаюсь до учнів: будьте уважними та активними, і в нас все вийде. Бажаю успіху!

До того як розпочнеться урок, зосередьтесь і подумайте, що ви від нього очікуєте.

II. Перевірка домашнього завдання. Актуалізація опорних знань

1. Перевірка завдання, заданого за підручником

Декілька учнів на перерві записують розв’язання номерів, заданих додому, на дошці, а на уроці коментують свої розв’язання.

2. Виконання завдань на встановлення відповідності

Випробування полягає в підкиданні грального кубика. Установіть відповідність між подією (1-4), яка відбулася внаслідок цього випробування, та її ймовірністю (А-Д) (Слайд 2).

Перед тим, як перейти до вивчення нової теми, давайте згадаємо, що ви вже вивчили із елементів прикладної математики?

1.                Що таке середнє арифметичне декількох чисел?
2.                Як будують стовпчасті та кругові діаграми?

III. Мотивація навчальної діяльності

Історична довідка (Слайд 3)

«Статистика знає все» – такими словами розпочинається друга частина роману Іллі Ільфа і Євгенія Петрова «Дванадцять стільців». «Відомо, скільки якої їжі з’їдає в рік середній громадянин республіки… Відомо, скільки в країні мисливців, балерин, верстатів, собак усіх порід, велосипедів, пам’ятників, дівчат, маяків і швейних машинок… Як багато життя, повного запалу, пристрастей і думок, дивиться на нас зі статистичних таблиць. Від статистики не заховаєшся нікуди…»

Вчитель. Тепер я пропоную вам відгадати кросворд. Він не зовсім звичайний: деякі слова або може, навіть й усі, ви вже чули, але не уявляли собі, що вони мають відношення до математики. Перед кожним з вас лежать аркуші, на яких питання до кросворду. Ви уважно читаєте їх, підіймаєте руку й відповідаєте на питання, але обов’язково називаєте його номер. Якщо ви правильно розгадаєте кросворд, то у виділеному стовпчику зможете прочитати прізвище вченого, без якого не було б нашого сьогоднішнього уроку.

Вчитель. До речі, вам буде завдання: деякі терміни, які є основними при вивченні цієї теми не зустрічаються у нашому кросворді (вам необхідно буде доповнити їх та записати на дошці), а інші – зайві. Для цих слів треба дати відповідь на таке питання: з якого розділу, де зустрічаються? (Слайд 4)

1. Її показують манекенниці на подіумі, навіть існують її тижні у Парижі.

2. Серед птахів -  він найбільший у альбатроса (до 325 см). Цей термін використовується також у боксерів.

3. Відрізок, який поєднує вершину трикутника з серединою протилежної сторони.

4. Сума чисел, поділена на їхню кількість.

5. Вона буває малоймовірною, достовірною. Її величина не може бути більшою за 1.

6. Фізична величина, обернена до періоду.

7. Ділянка місцевості, обладнана для проведення навчальних стрільб, випробовувань озброєння й техніки. В математиці цей термін означає многокутник.

8. Відстань від початку відліку до точки, яка зображує це число на координатній прямій. Записується, наприклад, так │х│.

9. Вчений, який вперше ввів термін «статистика».

Примітка. Зайві слова: ймовірність, модуль. Ймовірність зустрічається у розділі «Теорія ймовірностей», модуль – «Координати у просторі», «Рівняння», «Нерівності».

Не вистачає слів: варіанта, гістограма, варіаційний ряд, об’єм.

IV. Вивчення нового матеріалу

За визначенням словника, статистика (лат. stato – держава) – наука, що вивчає кількісний бік суспільних явищ і процеси у нерозривному їх зв’язку з якісним змістом. (Слайд 5)

Статистика – це наука, що збирає, обробляє та вивчає різні дані, які пов’язані з масовими явищами, процесами, подіями.

Статистика виникла з практичних потреб людини, її господарської діяльності, необхідності обліку земельних угідь, майна, кількості населення, вивчення роду його занять, вікового складу тощо.

1.                Яким тиражем слід випускати підручник з алгебри для 9 класу?
2.                Скільки кілограмів риби і морепродуктів вживає в середньому за рік один житель України?
3.                Чи вигідно для концерту певного артиста орендувати стадіон?

На ці та багато інших запитань допомагає відповісти статистика.

Вчитель. На сьогоднішнім уроці ми з вами розглянемо математичну статистику та її основні поняття: вибірка, варіаційний ряд, розмах, мода, медіана, середнє значення , полігон, гістограма; навчимося складати частотні таблиці, знаходити міри центральної тенденції вибірки, будувати полігон частот та гістограми за допомогою комп’ютера.

Але спочатку послухайте повідомлення про людину, яка вперше використала слово «статистика». Саме його прізвище виявилося ключовим при відгадуванні кросворду.

Учень. (Слайд 6) Ахенваль – німецький філософ, економіст, історик, юрист, педагог, один з засновників статистики.

Готфрід Ахенваль народився 20 жовтня 1719 року в Ельбінзі(Німеччина) у родині бізнесмена.

З 1738 по 1743 роки навчався у Йєнському університеті ім. Ф.Шиллера, університеті Галле Віттенберг та Лейпцігському університеті.

 З 1746 року читав лекції студентам у Марбурському університеті. З  1748 року У Гьотінгенському університеті – професор філософії, права. Він викладав на кафедрі історії та статистики, яку ж сам і заснував.

Ахенваль вважається засновником статистики як науки тому, що він не тільки сформулював точне означення всіх її складових та визначив її задачі та цілі, а й тому, що він перший ввів у науковий обіг слово «статистика» в 1749 році.

Помер Г.Ахенваль 1 травня 1772 року у місті Гьотінгем. 

(Слайд 7)

У XX ст. з’явилась математична статистика – розділ математики, який присвячений методам збору й обробки математичних даних та їх використанню для наукових і практичних спостережень.

Тож сьогоднішній урок ми присвятимо вивченню елементів математичної статистики, а саме статистичних даних і способів подання даних.

Учні записують число, класна, робота, тему уроку.

При вивченні нового матеріалу учні працюють з опорним конспектом (Додаток 1), що є в кожного на парті.

(Слайд 8)

Статистичне дослідження складається із наступних етапів:

Розглянемо реалізацію кожного етапу на прикладі.

Коли ми проводимо дослідження, то частина отриманих даних в цьому випадку називається вибіркою. Вибірка—сукупність об’єктів, на основі яких проводять дослідження.

Постановка проблеми: Взуттєвій фабриці потрібно знати, скільки пар взуття і яких розмірів треба виготовити. Як це з’ясувати? (Слайд 9)

Шляхи вирішення проблеми: опитати всіх людей надто довго і дорого. Тому роблять вибірку: опитують вибірково кілька десятків або сотень людей. Ми опитали учнів нашого класу, а саме 25 чоловік.

Учень. (Слайд 10) В результаті опитування отримали вибірку із 25 даних, які занесені у таблицю на другому листі роздаткового матеріалу на ваших партах: 43, 38, 36, 46, 37, 42, 40, 38, 40, 40, 39, 38, 37, 43, 36, 37, 38, 38, 41, 42, 40, 36, 38, 39, 40.

Запишемо цю вибірку ще раз, впорядкувавши її елементи за величиною.

36, 36, 36, 37, 37, 37, 38, 38, 38, 38, 38, 38, 39, 39, 40, 40, 40, 40, 40, 41, 42, 42, 43, 43, 46

Такий спосіб запису вибірки називається варіаційним рядом, а кожне із значень називається варіантою.

Для зручності дані вибірки групують у класи (за розмірами взуття) і відмічають, скільки значень вибірки містить кожний клас (Слайд 11).

Такі таблиці називають частотними. В них числа другого рядка – частоти (показують, як часто трапляються у вибірці ті чи інші її значення).

Відносною частотою значення вибірки називається відношення частоти значення вибірки до кількості усіх значень вибірки, виражене у відсотках.

 У розглянутому прикладі  частота розміру взуття 37 дорівнює 3, а відносна частота – 12%, бо 3 : 25 = 0,12 = 12%.

За частотною таблицею можна побудувати полігон частот (Щоб візуально це побачити, побудуємо на координатній площині точки, де абсцисами будуть відповідні розміри взуття, а ординатами – частоти розміру, та сполучимо одержані точки) та гістограму, які ви можете бачити на слайді. Вони наочно показують, яку частину взуття бажано випускати того чи іншого розміру.

(Слайд 12)

Приклад 1. Полігон частот розподілу учнів класу по розміру взуття

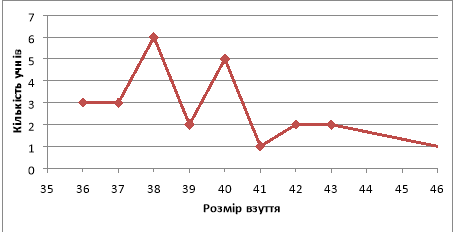
Приклад 2. Гістограма (стовпчаста діаграма)

(Слайд 13)

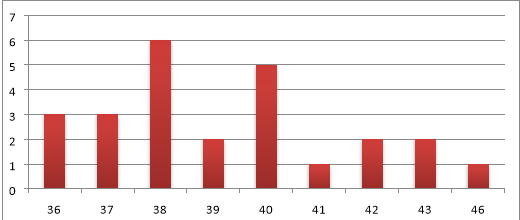
Приклад 3. Кругова діаграма розподілу учнів 9-го класу за віком (Слайд 14)

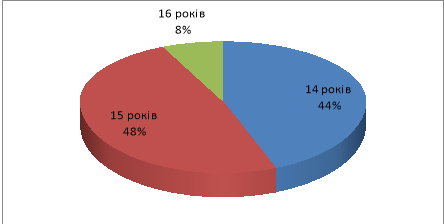
Отже, провівши дослідження для взуттєвої фабрики, можемо зробити висновок і порекомендувати випускати більше взуття 38 та 40 розмірів.

Зрозуміло, що одержані в такий спосіб висновки тільки ймовірні, наближені. Проте для практичних потреб цього буває достатньо.

Вибірки характеризують центральними тенденціями: модою, медіаною, середнім значенням.

Розглянемо їх на прикладі.

(Слайд 15)

Приклад. Учень 9 класу під час вивчення теми «Числові послідовності» отримав такі оцінки: 10, 10, 9, 11, 10, 8, 9, 10, 10, 9. Знайдіть середній бал учня.

Зрозуміло, що потрібно знайти середнє арифметичне всіх оцінок.

.

9,6 – середнє значення вибірки (середнє арифметичне усіх її значень).

Зверніть увагу, що середнє значення вибірки може не співпадати ні з жодним із її елементів. В прикладі середній бал 9,6, хоча всі оцінки виражені цілими числами.

Продивіться уважно ще раз на вибірку і скажіть, яку оцінку учень отримував найчастіше?

(Слайд 16)

Очевидно, найбільш часто він отримував оцінку «10». Така числова характеристика називається в статистиці модою.

Мода вибірки – це те її значення, яке трапляється найчастіше.

Можна сказати, що в цій вибірці наймоднішим є число 10.

На відміну  від середнього значення, яке можна обчислити для будь-якої вибірки, моди вибірка може і не мати.

Наприклад: 4, 5, 6, 7, 8.

Але вибірка може мати і дві моди: 2, 3, 4, 4, 5, 6, 6, 7, 8.

Ще одною важливою характеристикою вибірки є медіана.

(Слайд 17)

Медіана вибірки – це число, яке «поділяє» навпіл упорядковану сукупність усіх значень вибірки.

То ж упорядкуємо дану вибірку оцінок: 8, 9, 9, 9, 10, 10, 10, 10, 10, 11.

Оскільки вибірка має парне число значень, то медіана дорівнює півсумі двох її серединних значень. .

Якщо ж вибірка має непарне число значень, то медіана дорівнює числу, яке «поділяє» впорядковану вибірку навпіл. Наприклад, для вибірки з чисел: 1, 1, 2, 2, 3, 3, 4, 4, 4, 5, 6 медіаною є число 3.

Таким чином я можу сказати, що чим більший арсенал методів обробки даних, тим більш об'єктивний висновок можна отримати.

Фізкультхвилинка «Кольори» (Слайди 18-24)

V. Первинне застосування знань у стандартних ситуаціях

Початковий рівень коментує графіки, таблиці, гістограми (Слайд 25).

№ 1. Користуючись діаграмою, у якій відображено площі найбільших водосховищ України, установіть:

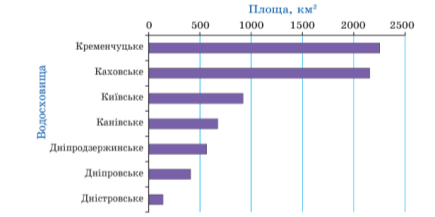
(Слайд 26)

№ 2. Користуючись діаграмою, на якій зображено відсотковий вміст солі у воді деяких водойм, установіть:

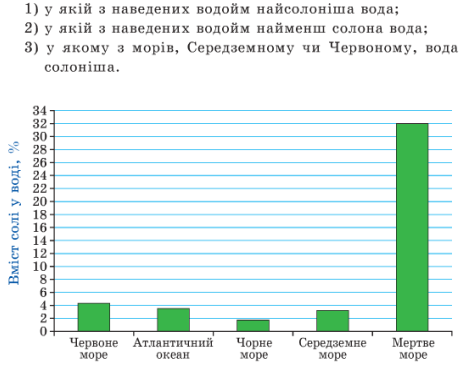
Робота в парах (Слайд 27)

Виконання письмового завдання

Завдання. Зріст учнів нашого класу (у сантиметрах) подано на листі 2 роздаткового матеріалу.

1. Скласти варіаційний ряд.
2. Скласти частотну таблицю.
3. Побудувати гістограму.
4. Знайти центральні тенденції вибірки:

1. Середнє значення;
2. Моду вибірки;
3. Медіану вибірки.

(Слайд 28)

Відповідь до завдання:

1. 140, 145, 149, 150, 153, 153, 155, 156, 158, 162, 162, 165, 165, 166, 167, 168, 168, 173, 175, 175, 175, 175, 178, 180, 190.

2.  
3. Гістограма
4. 

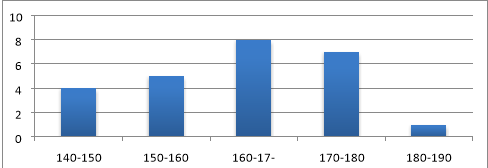
1) Середнє значення вибірки: 164,1 см.

2) Мода вибірки: 175.

3) Медіана вибірки: 165.

Середній і достатній рівень визначають центральні тенденції вибірки.

№24.5

№24.14 (Додаткове)

VI. Підсумки уроку. Рефлексія

Сьогодні ми з вами розглянули математичну статистику, її основні поняття.

Тестова перевірка знань учнів (Слайд 29-34)

1.Статистика – це наука про:

1. отримання й оброблення кількісних даних;
2. оброблення й аналіз кількісних даних;
3. отримання й аналіз кількісних даних;
4. отримання, оброблення й аналіз кількісних даних.

2.Статистика характеризує:

1. явища певної групи;
2. деякі явища;
3. поодинокі явища;
4. масові явища.

3. На 1 етапі проводять збір даних, що називають:

1. графіком;
2. таблицею;
3. частотою;
4. вибіркою.

4. Центральні тенденції вибірки - це

1. частота;
2. таблиці;
3. графіки;
4. середне значення, мода та медіана.

5.Стовпчаста діаграма – це

1. голограма;
2. сектограма;
3. мамограма;
4. гістограма.

6. На 2 етапі статистичних досліджень способами подання даних виступають:

1) схеми;

2) малюнки;

3) описи;

4) графіки, таблиці, діаграми.

Діти, ви сьогодні дуже добре попрацювали на уроці. Тому і результат маємо добрий. Ви всі були активні, уважні, працьовиті. Оцінювання учнів.

VII. Домашнє завдання (Слайд 35)

Вивчити опорний конспект; п. 24, № 24.6, 24.8, 24.12.

Творче завдання. Провести шкільне статистичне дослідження :

•                  І варіант «Кількість часу, проведеного за комп’ютером»
•                  ІІ варіант «Кількість часу, витраченого на виконання домашніх завдань»

Для отриманих даних треба створити частотну таблицю, знайти центральні тенденції вибірки та побудувати гістограму або полігон частот.

(Слайд 36)

Додаток 1

Опорний конспект

Частотна таблиця

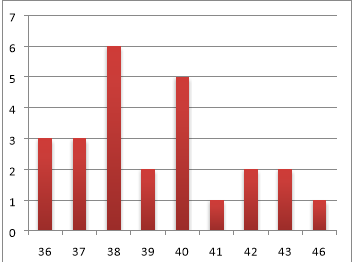Приклад 1. Полігон частот розподілу учнів класу по розміру взуття

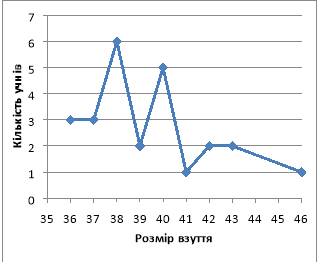Приклад 2. Гістограма (стовпчаста діаграма)

Додаток 2

Таблиця результатів вимірювання ваги і зросту учнів 9-го класу