Урок для учнів 8 класу "Теорема Піфагора"

Про матеріал

Урок по змішаному навчанню. Учитель заздалегідь ділить учнів класу на три групи. Після виконання завдання певного етапу уроку групи міняються місцями, таким чином, кожна група спробує свої сили у кожному виді робіт.

Перегляд файлу

Тема: Теорема Піфагора

Мета:

Навчальна: сформувати в учнів розуміння змісту теореми Піфагора та її доведення, познайомити учнів з біографією та діяльністю Піфагора

Розвивальна: розвивати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв'язування задач на знаходження невідомих сторін прямокутних трикутників, розвивати пам'ять, математичну логіку, уміння користуватись інтернетресурсами, цікавість до предмета

Виховна: виховувати взаємоповагу, уміння працювати в колективі.

Обладнання: презентація по темі, відеоролики про життя, діяльність Піфагора, планшети, мобільні телефони для виконання роботи онлайн, епіграф до уроку

Цільова група: учні 8 класу

Типу уроку: засвоєння нових знань.

Тривалість 90 хвилин (два уроки)

Хід уроку:

Епіграф до уроку:Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя (Піфагор)

Учитель заздалегідь ділить учнів класу на три групи. Після виконання завдання групи міняються місцями, таким чином, кожна група спробує свої сили у кожному виді робіт. На початку уроку на столах груп знаходяться пронумеровані запитання (по два в кожній групі), учні по черзі читають запитання, та дають відповідь на нього.

Що називається трикутником?
Які види трикутників вам відомі?
Який трикутник називають прямокутним?
Як називаються сторони прямокутного трикутника?
Який трикутник називають прямокутним рівнобедреним (як при цьому називають бічні сторони такого трикутника)?
Назвіть градусні міри кутів рівнобедреного прямокутного трикутника.

Сьогодні ми з вами познайомимось з однією чи не самою популярною теоремою, яку точно знають ваші батьки, і про яку неодноразово чули і ви – Теоремою Піфагора. Існує багато легенд про цього видатного вченого та філософа, про його винаходи, та про саму теорему, що носить його ім’я. Але чи сам він довів цю дивовижну теорему? А може вона була відома задовго до відкриття її Піфагором? Пропоную вам переглянути короткий відеоролик про Піфагора, щоб про це дізнатись. (відеоролик)

Як ви зрозуміли, теорема, що носить ім’я Піфагора була відома ще задовго до того часу, як сам вчений її довів. Існують факти, які стверджують, що давньогрецькі геодезисти використовували набор цифр 3,4,5 для створення квадратних кутів, для цього вони користувались мотузкою, поділеною гудзами на 12 рівних частин. Єгипетські жриці також знали таємницю такого трикутника і свято її берегли, вважаючи це даром Богів. Тому, коли Піфагору вдалось довести цю теорему, він приніс в жертву Богам 100 биків, вважаючи своє досягнення дарунком вищих сил. А трикутних зі сторонами 3, 4, 5 з давніх пір носить назву – єгипетський. Отже, чарівна теорема Піфагора звучить так: Квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів.

Американський шанувальник математики Луміс зібрав і опублікував (1968р) 367 видів доведень цієї теореми. Ми ж з вами, на уроці, познайомимось лише з декількома з них. Працювати будемо в групах. Перша група працюватиме зі мною, і ми разом доведемо теорему; друга вивчатиме доведення за QR-кодом, якій отримали і, нарешті, третя група опрацьовуватиме дану теорему за підручником.

Алгебраїчне доведення

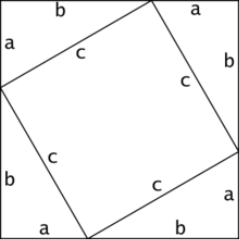
Чотири однакові прямокутні трикутники розташуємо так, як це зображено на малюнку.
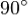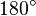Одержимо чотирикутник зі стороною с. Даний чотирикутник - квадрат, оскільки сума двох гострих кутів $90^\circ$ , а розгорнутий кут — $180^\circ$ .
Площа всієї фігури рівна, з одної сторони, площі квадрата зі стороною «a+b», а з іншої — сумі площ чотирьох трикутників і внутрішнього квадрата.

$(a+b)^2=4\cdot\frac{ab}{2}+c^2;$

$a^2+2ab+b^2=2ab+c^2;\frac{}{}$

$c^2=a^2+b^2;\frac{}{}$

За подібністю трикутників

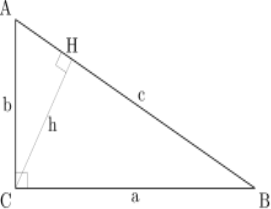
Нехай ABC — прямокутний трикутник, в якому кут C прямий, як показано на малюнку. Проведемо висоту з точки C, і назвемо H точку перетину з стороною AB. Утворений трикутник ACH подібний до трикутника ABC, оскільки вони обидва прямокутні (за визначенням висоти), і в них спільний кут A, очевидно третій кут буде в цих трикутників також однаковий. Аналогічно міркуючи, трикутник CBH також подібний до трикутника ABC. З подібності трикутників: Якщо

$BC=a, AC=b, \text{ and } AB=c, \!$

тоді $\frac{a}{c}=\frac{HB}{a} \mbox{ and } \frac{b}{c}=\frac{AH}{b}.\,$

$a^2=c\times HB \mbox{ and }b^2=c\times AH. \,$

Якщо додати ці дві рівності, будемо мати:

$a^2+b^2=c\times HB+c\times AH=c\times(HB+AH)=c^2 .\,\!$

Отже, Теорема Піфагора:

$a^2+b^2=c^2.\,\!$

Адитивний метод

(метод розкладу)

Існує цілий ряд доведень теореми Піфагора, в яких квадрати, побудовані на катетах і на гіпотенузі, розрізають так, що кожної частини квадрата, побудованого на гіпотенузі, відповідає частина одного з квадратів, побудованих на катетах. У всіх цих випадках для розуміння докази достатньо одного погляду на креслення; міркування тут може бути обмежене єдиним словом: "Дивись!", Як це робилося в творах стародавніх індуських математиків. Слід, однак, зауважити, що насправді доказ не можна вважати повним, поки ми не довели рівності всіх відповідних один одному частин. Це майже завжди досить важко зробити, однак можна (особливо при великій кількості частин) не дивлячись на те, що потребує це досить тривалої роботи.

Отже, ви вже досконало опрацювали теоретичний матеріал, і час застосувати набуті знання до розв’язування задач. Працюємо, знов таки в групах. Перша група – працює під керівництвом вчителя, друга група за посиланням, відшуковує завдання, розв’язує їх та надсилає готові відповіді, третя група розв’язує задачі за підручником,

Завдання для першої групи:

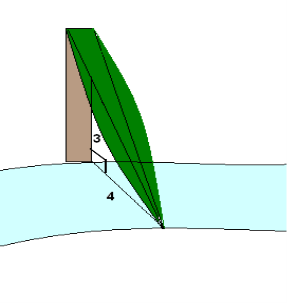
Задача№1 індійського математика ХІІ століття Бхаскари

«На березі річки росла самотня тополя. Раптом налетівши вітри зламали її стовбур.

Бідна тополя впала, утворивши кут між стовбуром і поверхнею води річки. Запам’ятай тепер, що в цьому місці річка у чотири лише фути була шириною. Верхівка зламалася, залишивши всього три фути від усього стовбура.

Прошу тебе, швидше мені скажи, яка висота тополі?»

Задача№2 Історія однієї шхуни

Одного разу до порту припливла шхуна, що потрапила у бурю. У неї відірвався і загубився трос, який з’єднував матчту та корму. І команді шхуни треба було як можна швидше відремонтувати її…

Завдання для другої групи: Для вас створено тестові завдання, опрацювати які можна на своєму смартфоні: ви отримали посилання (https://goo.gl/forms/0rkcNA8MpIDOgVCw1 ), переходьте за ним,обирайте вірну відповідь, надсилаєте її, та відразу ж побачите свої результати.

1. Квадрат гіпотенузи будь-якого трикутника дорівнює сумі квадратів катетів

а) так б) ні

2. Катет прямокутного трикутника дорівнює кореню квадратному з різниці квадрата гіпотенузи та квадрата катета

а) так б) ні

3. Трикутник, в якому квадрат більшої сторони дорівнює сумі квадратів менших сторін – прямокутний

а) так б) ні

4. Знайдіть гіпотенузу прямокутного трикутника, якщо катети відповідно рівні 3 і 4?

а) 5 б) 25

5. Знайдіть катет рівнобедреного прямокутного трикутника, якщо квадрат гіпотенузи 3200?

а) 160 б) 40

6. Знайдіть кути рівнобедреного трикутника, якщо його сторони a, b, c співвідносяться, як с²=а²+b² і с – найбільша сторона

а) 45⁰; 45⁰; 90⁰ б) 30⁰; 60⁰; 90⁰

Завдання для третьої групи: О.С. Істер Геометрія 8 клас, Київ, Генеза 2016 стр. 124-125 №№ 629; 635; 639

Теорема Піфагора є тим золотим ключиком, який дозволяє відкрити двері до багатьох загадок та задач, дає можливість виконувати наукові розрахунки траєкторій польоту літаків і ракет, руху небесних тіл, розрахунки можливих відстаней, висоту будівель. Цю теорему називають вічною. Їй понад 2 тисячі років. В середньовіччя її називали «ослячим містком», на честь учнів (їх прозивали віслюками), які запам’ятовували теорему без розуміння, та не могли перейти через місток – теорему Піфагора. Носила теорема Піфагора і іншу назву – теорема «нареченої». Справа в тому, що в деяких списках «Начал» Евкліда ця теорема називалась «теоремою німфи» за схожість креслення з бджілкою, метеликом, що грецькою називалось «німфа», цим же словом греки називали богинь та молодих жінок і наречених. Перекладаючи з грецької, арабський перекладач переклав слово «німфа» як «наречена», а не «метелик», так з’явилась лагідна назва «теорема нареченої». А вже радянські діти придумали вірш, який відображав саму суть теореми – «Піфагорові штани на всі сторони ровни»

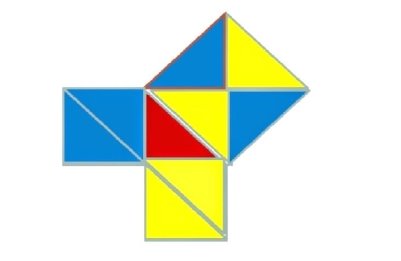
Отже, ще раз складемо теорему Піфагора, що записана на окремих частинах одного зображення, тим самим складемо й саме зображення.

Хто може назвати цей музичний інструмент? Це - МОНОХОРД, музичний інструмент, що являє собою дерев’яний ящик з однією струною. Його вважають пробатьком всіх сучасних струнних інструментів, в тому числі фортепіано Блискучим музикантом, винахідником такого інструменту по праву вважають Піфагора. Математичне дарування в поєднанні з феноменальним музичним слухом і чуткою научною інтуїцією дозволило Піфагору першим здогадатись про таке явище, як натуральний (природний) звукоряд. Затискаючи струну у відмічених місцях, Піфагор з’ясував, що між довжиною отриманих відрізків та довжиною цілої струни існує певне математичне відношення. Піфагор першим зрозумів, що приємні слуху 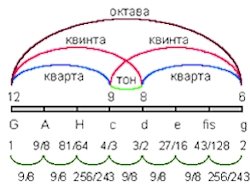Математическое соотношение звучання бувають лише в тому випадку, коли довжини струн, що створюють ці звуки, відносяться як цілі числа першої четвірки 1:2 2:3 3:4 (так визначились перші музичні інтервали октава, квінта та тризвучча)

Похожее изображение А щоб нам не бути тими «прадавніми віслючками» пригадаймо ще раз про що ж ми говорили на уроці. Пригадувати будемо переглядаючи відео (канал TEDеD, планіметрія,кінозал, TED, 8 клас) англійською мовою, в ролику все те, про що ми вели мову на уроці, і ви, крім матеріалу сьогоднішнього уроку зможете перевірити й свою англійську. А вже, для тих учнів, які англійською ще не дуже володіють в ролику буде переклад.

Домашнє завдання : 1.Вирізати з паперу 3 квадрати зі сторонами, що дорівнюють сторонам накресленого на папері прямокутного трикутника, і за допомогою розрізування, впевнитись, що площа найбільшого квадрата дорівнює сумі площ менших. 2.Придумати практичну задачу на теорему Піфагора, та розв’язати її.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Шевчук Валентина Петрівна

Пов’язані теми

Алгебра, 8 клас, Розробки уроків

Додано

26 квітня 2020

Переглядів

950

Оцінка розробки

Відгуки відсутні