Урок ,,Функції. Властивості функцій''. 10 клас

План-конспект уроку з математики

10 клас. Тема уроку: Функції. Властивості функцій.

Мета

освітня: формувати математичну компетенцію; узагальнити та систематизувати знання учнів за темою  «Функції. Властивості функцій», досліджувати графік функції та робити висновки; формувати вміння використовувати набуті знання на практиці;

розвивальна: розвивати вміння аналізувати, узагальнювати, робити висновки; розвивати почуття патріотизму, ознайомити з історією, звичаями та традиціями рідного краю, духовно збагатити.

виховна: формування поведінкових компетенцій, навичок роботи в групі, парах, індивідуальної роботи, навичок об’єктивного  самооцінювання.

Технічне обладнання та програмне забезпечення:  презентація, мультимедійна   дошка,  креслярські інструменти, набір магнітів.

Тип уроку: урок практичного застосування знань, умінь і навичок.

Вид уроку: урок-дослідження.

Немає жодної галузі людського знання, куди не входили

 б поняття про функції та їх графічне зображення

К. Ф. Лебединцев

Хід  уроку

Ι. Організаційний  момент.

Учитель. Сьогодні ми спробуємо використати набуті знання на практиці як майбутні фахівці своєї держави – України. Один відомий політичний діяч казав, що Україна на карті схожа на людське серце, перетнуте аортою Дніпра (Слайд 3).  Як серце важливе для людини, так для нас повинна бути важлива наша земля. Бо це не просто земля, вода, гори, трава. Це наше сьогодення  і наше завтра. Щоб розуміти  сьогодення, слід добре знати минуле. А що ми знаємо про нашу державу? Властивості функцій допоможуть нам згадати нашу історію, звичаї, пам’ятки, національні традиції рідного краю, описати різні процеси, а головне пишатися тим,  що ми є громадянами такої великої держави. Визначається експерт-помічник учителя – один з учнів, клас  об’єднується  у групи: 1) теоретики-дослідники; 2) практики.

ΙΙ. Повідомлення теми і мети уроку.

Мотивація  навчальної  діяльності.

(Учні в парах обговорюють отримане завдання, складають логічний ланцюжок, формулюють тему уроку.) 

Учитель. Усім цікаво, чому на дошці не записано тему сьогоднішнього уроку? Маленька підказка: тема уроку замаскувалася у вигляді ментальної карти (Слайд 4), яку вам  потрібно було зробити. Представники груп презентують свої результати.

Отже, тема уроку -  «Властивості функції».

Учитель. Теоретичний матеріал із цієї теми ми з вами вивчили на попередньому уроці,  а сьогодні попрацюємо над його закріпленням.

 У кожного з вас лежить смайлик-стікер без обличчя.  Намалюйте ваші емоції, підпишіть цей смайлик та поміркуйте, яку з цілей ви ставите перед собою на цьому  уроці. Розмістіть свій стікер у відповідному секторі діаграми на дошці настрою.

ΙΙΙ.  Перевірка домашнього завдання.

На попередньому уроці ви отримали завдання,  зміст якого полягав в опрацюванні тестових завдань з теми та додаткового  творчого завдання. Зараз ми перевіримо правильність виконання першої частини, а творчість ви будете мати  змогу продемонструвати під час уроку.

(Перевірка   домашнього   завдання  за записаними на дошці або підготовленими до показу слайдами  презентації  із правильно виконаними вправами домашнього завдання).

Учитель. Запишіть отриману вами кількість балів у таблицю  «Картка оцінювання» (додаток 1) навпроти графи «Домашнє завдання». За правильно виконані вправи можна отримати по 1 балу.

ΙV. Закріплення вивченого матеріалу  (таксономія  Блума)

Блок 1. Знання

(Учні переглядають теоретичний матеріал, вивчений на попередньому уроці, та формулюють  основні властивості функції.)

Група  «Теоретики- дослідники »

1. Функція називається зростаючою, якщо більшому значенню аргумента відповідає більше значення функції. На малюнку 1 зображено графік функції у = f(x), що зростає на проміжку [а; b].
2. Функція називається спадною, якщо більшому значенню аргумента відповідає менше значення функції. На малюнку 2 зображено графік функції у= f(х), що спадає на проміжку [а; b].

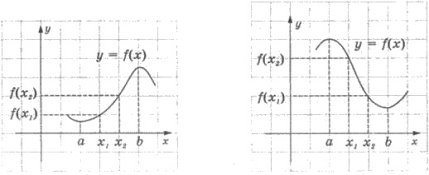
мал..1                                                  мал.2

3. Точку х₀  називають точкою максимуму функції  у = f(x), якщо для всіх з деякого околу точки х₀  виконується нерівність  f(х₀) > f(x).

Значення функції в точці максимуму називають максимумом функції. На малюнку 1 х = b - точка максимуму функції, а на малюнку 2  х = а - точка мінімуму функції.

Точку х₀  називають точкою мінімуму функції у = f(x), якщо для всіх х з деякого околу точки х₀ виконується нерівність f(х₀) < /(х). 

Значення функції в точці мінімуму називають мінімумом функції. На малюнку 1 х = а - точка мінімуму функції, а на малюнку 2 х = b - точка максимуму функції.

4. Точка, яка відокремлює опуклу частину неперервної кривої 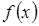 від угнутої, називається точкою перегину .

На мал. 2 точка  М₀   є точкою перегину.

 

Учитель.  Функція – одне з найважливіших понять математики, вона дає можливість досліджувати і моделювати не тільки стани, а й процеси. Дослідження процесів і явищ за допомогою функцій – один з основних методів сучасної науки.

Цікаво, а  чи  знаєте  ви як використовуючи малюнок  за графіком функції знайти основні властивості функції? Перевіримо знання за допомогою  малюнків-завдань.

Блок 2. Розуміння

(Учні працюють із робочим зошитом (додаток 1) та виконують завдання 1.Самоперевірка з коментуванням, виставлення балів в аркуш оцінювання.)

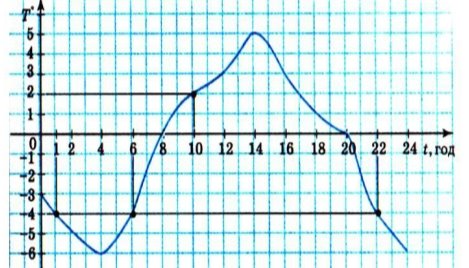
Завдання 1. За допомогою графіка температури повітря у Києві протягом доби визначити:

1. Якою  була температура  0 10 годині?

2. О  котрій годині температура була -4⁰ С?

3. Чи є крива лінія, зображена на малюнку, графіком функції?

4.  Яка її область визначення?

5.  Яка її область  значень?

6. Як поводить себе графік функції на проміжку (1;6), (6;10)?

7. При  якому значенні аргумента функція приймає найбільше значення?

8. При якому значенні аргумента функція приймає найменше значення?

Група  «Теоретики- дослідники »

Мало кому відомо, що Київ – найдрівніша столиця світу. Уся наша цивілізація починалася з Київських земель біля 7500 років тому.

Учитель. Український народ дуже працьовитий. У сільській місцевості і в наш час основними є аграрні роботи, в містах люди працюють на заводах фабриках, шахтах, видобувають вугілля, нафту. Українці- землеробці вміли добре оброблювати землю,сіяти, жати  і випікати хліб. Саме відношенням до праці українці вимірювали ,чим є людина, і засуджували  або зневажливо відносилися до ледарів.

Задача 2.  За поданим малюнком (Слайд.5) знайти:

1.У які роки виробництво зерна в Україні зазнало спад, а у які роки відбувся приріст?

Група  «Практики»

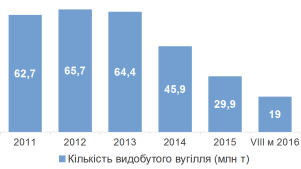
Задача 3. Побудувати  стовпчату діаграму росту видобутку вугілля(в млн.т) в Україні за останні роки за поданими даними: (Слайд.6)

Блок 3. Застосування знань.

Щоб проілюструвати характерні властивості функції звернемося до усної  народної творчості. Отже прислів’я – це відображення стійких закономірностей, що перевірено багатовіковим досвідом народу. Аналогія з прислів’ями дозволить нам краще зрозуміти певні  властивості функції та  запам’ятати їх.

Завдання 4. Кластер

До поданих графіків функцій підберить прислів’я , що розкривають зміст процесів функцій.  (Слайд7), (Слайд 8).

Завдання 5 . Група  «Практики».

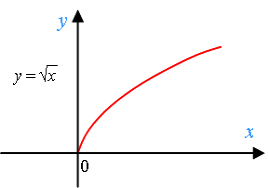
«Чим  далі в ліс, тим більше дров», говорить прислів’я. Зобразити  графіком, як  зростає кількість дров по мірі просування у глиб ліса.

Горизонтальна вісь графіка - це лісна дорога . По вертикалі будемо відкладати кількість дров на даному кілометрі. Графік  показує собою кількість дров як функцію шляху.

Група  «Теоретики»

Відповідно до прислів’я, ця функція незмінно зростає. Які дві точки на вісі абсцис не обрати , для більш дальньої (чим далі в ліс…) значення функції будуть більше (…тим більше дров). Така властивість функції має назву монотонне зростання.

Необхідно   відчути  різницю між монотонним зростанням і монотонним спаданням. Зростання – це рух тільки верх. Неспадання – рух або вверх, або ні верх ні вниз.  Зростання- частковий  випадок не спадання. Наприклад, усюди постійна функція належить до неспадних, але ж вона ні на одному проміжку своєї області визначення не зростає.

Група  «Практики».

Прислів’я   «Вище міри кінь не стрибає». Якщо зобразити траєкторію коня, що скаче графічно, то висота стрибків в повній відповідності з прислів’ям буде обмежена зверху деякою  «мірою» (мал.3 ).

 

Група  «Теоретики-дослідники»

Ця властивість притаманна функціям sinx і cosx. Тут також є своя  «міра» , за межі якої не виходять хвилі синусоїди і косинусоїди. Графіки цих функцій знаходяться у полосі між прямими у=-1 і у=1.

Прислів’я    «Пересів гірше недосіва». Віковий досвід свідче: врожай лише до деякої міри росте разом з щільністю посіва, далі він знижується , тому що за  надмірну гущу паростки  починають  глушити одне одного. Ця характерність стане особливо наочною, якщо зобразити її графічно, де врожай представлено як функція щільності посіва (мал.4).

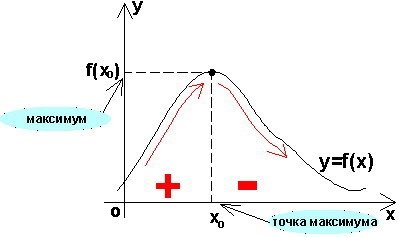
                                 мал.4

Врожаю максимально, коли поле засіяно в міру. Максимум –це  найбільше значення функції в порівнянні з її значеннями у всіх сусідніх точках. Це як вершина гори , з якої усі дороги ведуть тільки вниз, куди не йди. Є у максимума антипод-мінімум. Мінімум- це як впадина, з якої куди не йди – усі шляхи ведуть тільки вверх. Але, якщо йти все далі, зростання десь зміниться спаданням(мал.5).

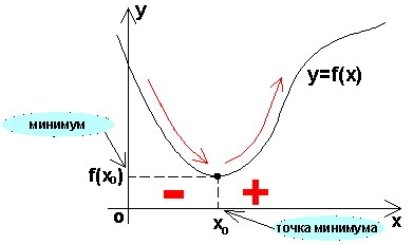
                                 мал.5

Учитель.  Сучасне життя неможливо уявити без повторюваності.  У навколишньому середовищі  будь-яку повторюваність називають  періодичністю. Але повторюваність може бути більш або менш строгою.

Завдання 6.  Павутинка дискусії .

Дослідіть та обґрунтуйте, чи можна вважати вираз  « періодичне видання» строгим ?  Газети  виходять день за днем . Журнали друкуються з місяця в місяць, з тижня в тиждень. Строгість поняття періоду тут  досягається чи ні з математичної точки зору?

Група  «Теоретики»

Відповідь:  Але ж абсолютної строгості поняття періоду тут не досягається. Воно  було б тут лише тоді, коли б час виходу було дотримано з  абсолютною точністю, а тексти повністю співпадали. Бездоганні приклади періодичності у змозі дати тільки математика. Наприклад, тригонометричні функції є прикладами періодичних функцій.

Групам пропонується привести приклади природних явищ, роботу підприємств, приклади з  життя і техніки в нашій країні, в яких би чітко мала прояв періодичність.

Завдання 7. Дослідити властивості функції за допомогою завдання «Шляхами України».

Гра складається з того, що «водію» з кожної команди потрібно «проїхати» дорогу і  пояснити всі її ділянки мовою водія і математика і згадати усі символи нашого краю які нам зустрінулися. Відправляємося в путь на автомобілі по шосе містами України. Будемо уважно додивлятися до рельєфу дороги (Слайди.)

Учень від групи  «практики»: Рівна ділянка  дороги асоціюється з терміном « константа» (Слайд 9). Їдемо далі і бачимо річку-(Дніпро)-Славутич.Вона тече через всю Україну і через всю її історію. Дніпро оспіваний у піснях, думах, легендах і є нашою національною гордістю, славою України.(Слайд 10).  Дорога йде під уклін –це монотонне спадання. Закінчився спуск, і водій зупиняється, відмічаючи тим самим точку мінімума.(Слайд 11). Дорожний знак вказує підйом, а у математика напоготові свій термін –монотонне зростання. Мандруючи рідною Україною, проїзжаємо гору Говерлу, що знаходиться в Карпатах (Слайд 12),знають її по всій Україні, тому що це найвища гора на українській землі. Перевалили через вершину  – пройдена точка максимума. І знов почалося монотонне спадання,  спуск.

На холмах дорога випукла, в ложбінах вогнута (Слайд 13). Не відмічені дорожними знаками стики таких ділянок дороги математик відмітить про себе як точки перегину. Завершуємо нашу подорож острівом Хортиця-фактична частина міста Запоріжжя,дорогий серцю кожного українця символ козачества, відомої Запорізської Січі (Cлайд 14). А відомо вам, що самий довгий історичний шлях проходив через українську територію-«шлях з варяг у греки». Довжина його нараховувала 3 тисячі кілометрів. Була побудована унікальна система річних шляхів, що зв’язувала Стародавню Русь з южно-руськими землями, і Чорне море  - з Балтійським.

Тому, Київська Русь слугувала своєрідним мостом між Східною Європою і Стародавнім Востоком. (Слайд 15).

Блок 4. Аналіз.

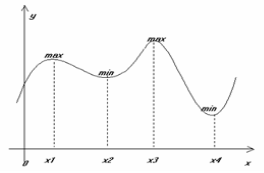
Учень від групи «теоретики»: Математичні поняття, про які йшла мова, поділяються на дві групи. Одні описують поведінку функції в околі деяких характерних точок (максимум, мінімум, перегин ), інші – в деяких проміжках (опуклість, вогнутість, зростання, спадання). Отже, щоб відтворити профіль шляху, достатньо описати поведінку функції спочатку в околі характерних точок, а потім в проміжках між цими точками. Схематично зобразити профіль дороги можна так:

Блок 5. Оцінка

Метод  «Капелюхи мислення Едварда де Боно»

(Учні працюють у мотиваційних групах, узагальнюють результати роботи.)

 Учитель . Функції. Графіки  функцій проявляють  себе чи не в кожній сфері нашого життя. Придивіться уважніше і скажіть, чи помічали все це раніше. Навіть геометричні узори, що використані в орнаменті української  вишиванки, а саме хвилясті лінії нагадують графік функції (Слайд 16).

Учитель. Підрахуйте набрані бали в картці оцінювання. Здайте ваші друковані зошити з балами. Пам’ятаєте, на початку уроку ми ставили мету дослідження. Тепер об’єднайтеся у групи за спільними поглядами, приміряйте капелюхи  Едварда де Боно і підбийте підсумки виконаної роботи.

(Учитель виставляє додаткові бали за творчі завдання й повідомлення, оцінює активність учнів тощо.)

VΙ. Домашнє завдання: Намалювати герб України на координатній площині. Лінії трезубца порівняти з графіками основних функцій. Що означає цей символ?

VΙΙ. Підсумок уроку: «Не чого вчився, а чого навчився».

Якщо ви реалізували поставлену мету, то можете забрати свої смайлики як трофей за здобуті цінні знання. Виставляються бали за урок. Подяка учням за роботу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Список використаних джерел

1.Гайдай Л.Історія України в особах, термінах, назвах і поняттях.-Луцьк: Вежа,2000.

2.Довідник з історії України/ За ред.І.Підкови та Р.Шуста.-Київ: Генеза, 1993.

3. Палієва С.Математика. Квести. 5-11 класи.-Київ: Видавничий дім  «Перше вересня»,2017.

4. Сучасний  урок/Упоряд.: Ж.Сташко,О.Гринько.-Київ: Вид. Група , «Шкільний світ», 2016.

5. Інтерактивні технології навчання.\\ Помету О., Пироженко Л. Сучасний урок: Інтерактивні технології навчання: наук. Метод. Посібник. –  К.: А. С. К., 2004. – с. 33-42.

6. http://5fan.ru/wievjob.php?id=55330

7. Математика. Довідник\ Сост. Г. М. Якушєва; 1997.

8.Коваленко В.Г. Дидактические игры на уроках математики. Книга для учителей. –Москва «Просвещение», 1990.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

Робочий Зошит

Дата ____ПІ_________________________ Тема уроку____________

Картка оцінювання

№	Вид діяльності	Набрані бали
1	Перевірка домашнього завдання
2	Завдання 1
3	Завдання 2
4	Завдання 3
5	Завдання 4
6	Завдання 5
7	Завдання 6
8	Завдання 7
9	Творче завдання
Загальний бал за урок