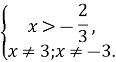Урок "Функція. Область визначення, область значень та графіки функцій."

Тема. Функції. Область визначення, область значень та графіки функцій.

 

Мета:  узагальнити, систематизувати знання, вміння, навички студентів з теми «Функції»; розвивати мислення, увагу, пам'ять; виховувати інтерес до математики.

 

Тип заняття: узагальнення і систематизації знань, умінь і навичок.

 

     Обладнання: підручники Г.П.Бевз, В.Г.Бевз Математика 10,  

                    М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук Алгебра і 

                     початки аналізу, таблиці, роздатковий матеріал, 

                     креслярські  приладдя, мультимедійний комплекс.

                               А те, що гідне існувати,

 гідне бути знаним

                                                              Ф. Бекон

 

Хід заняття

І. Організаційний момент.

II. Повідомлення теми і мети заняття

Сьогодні  ми знову полинемо у світ, де є особлива залежність змінної у від змінної х, де в задачах відображене людське буття, тобто у чарівний світ алгебри. Ми глибше пізнаємо істину.

«А те, що гідне існувати, гідне бути знаним» -  сказав англійський філософ Ф. Бекон (1561-1626)

Ці  слова  можуть стати  епіграфом до подальшого пізнання світу математики. Сьогодні  наші напрацювання постануть із сторінок усного журналу «Голос математики». Наскільки гучним буде цей голос, залежить від вас, ваших знань, умінь, бажань, зібраності на занятті.

Процеси реального світу тісно пов'язані між собою. Серед різноманітних явищ вчені виділили такі, в яких взаємозв'язок величин дуже тісний. Знаючи значення однієї величини можна визначити значення іншої. З поняттям функцій та  властивостями деяких функцій ви вже знайомі. Згадаємо і повторимо деякі відомості про функції.

Зауваження. Перед вивченням теми  студенти одержали завдання: повторити функції та їx властивості, які вивчались у 7 та 8 класах; підготувати історичний матеріал з даної теми.

Усний журнал.

Сторінка перша (екскурс в історію).

«3 математичних джерел».

Ідея функціональної залежності сягає у сиву давнину, коли люди  тільки-но починали розуміти існування залежностей у природі, у праці, у побуті. Як і багато інших наукових понять, поняття функції виникло із практичних потреб людини. Перші таблиці в Стародавньому Вавилоні (4-5 тис. років тому), Єгипті,вивчення залежностей між відрізками у крузі в Стародавній Греції тощо – все це свідчення застосування функціональних залежностей.

Французький вчений Оресм (XVI  ст.) уже  дає  графічні  зображення залежностей,  робить спробу класифікувати  їх, вивчає характерні властивості найпростіших  графіків.  XVI-XVH ст. ознаменувалися  глибокими змінами  у природознавстві. У  математиці, яка досі  мала справу здебільшого зі сталими величинами, з'явилася  необхідність у створенні  нових  математичних методів для опису рухомого світу. Знадобилося  поняття  змінної величини, яке ввів  у науку французький  філософ і  математик Рене Декарт (1596-1650). Для запису залежностей між величинами Декарт почав застосовувати букви, а відношення між відомими та невідомими зображав у вигляді рівнянь.

Наприкінці XVII ст. німецький математик, фізик, філософ Г. Лейбніц (1673р.) ввів термін  «функція» (від  латинського  functio  -  здійснення, виконання) у розумінні величини, що вказує ту чи іншу функцію, і  позначав х¹; х² (у сучасних позначеннях f₁(x); f₂(x)) Лейбніц  користувався переважно геометричним трактуванням поняття функції.

Швейцарський математик І.Бернуллі (1718р.) дав означення функції без геометричної інтерпретації.

Англійський математик, фізик, астроном І.Ньютон (1643 - 1727) поняття функції пов'язував з механічними уявленнями.

Л.  Ейлер (1707 - 1783) у книзі «Введення в  аналіз» (1748р.) уточнює

означення функції: «Функція змінної кількості є аналітичний вираз, складений якимось чином з цієї змінної кількості І чисел або сталих кількостей».

Хоча до XIX ст. не було повного і точного означення функції, все ж існуючими поняттями досить  довгий  час  користувалися з  успіхом  і  в математиці, і в механіці, і в інших галузях.

На початку XIX ст. чимало математиків роблять спробу дати загальне та точне означення функції. Французький математик С.Лакруа (1765-1843) писав у 1810р.: «Всяка кількість, значення якої залежить від однієї або багатьох кількостей, називається функцією цих останніх  незалежно від того, відомо чи ні, які операції треба застосувати, щоб  перейти від них до першої». Згодом чеський  математик Б.Больцано (1781-1848) у 1817 та 1839 р, німецький математик  П.Діріхле (1805-1859) у 1837 p., російський  математики  М.Лобачевский (1792-1856)  у  1834 р.  та інші вчені сформулювали більш  повне означення поняття функції.

У XX ст. вводяться так звані узагальнені  функції. Зв'язок математики з об'єктивним світом стає більш опосередкованим, вираз y=f(x) розглядають як дію над об'єктами різної природи.

Важливий  внесок у  розвиток  теорії   функцій внесли  українські математики М. Остроградський (1801-1862), В. Буняковський (1804-1889), М.Кравчук (1892-1942), Є. Ремез (1896-1975). В. Дзядик (1919-1998) та інші.

Більшість  природничих і суспільних явищ, процесів можна описати за допомогою функцій. Досліджуючи властивості функцій, маємо можливості ґрунтовніше пізнавати реальний світ.

III. Систематизація  й  узагальнення   основних  відомостей   про функцію, способи задання,  графіки функцій.

Сторінка друга.

«Теорія - фундамент знань»

Фронтальне опитування, яке проводиться у вигляді інтерактивної вправи «Мікрофон»

Рекомендації для викладача при проведенні вправи «Мікрофон»

1. Поставте запитання студентам.

2. Запропонуйте студентам якийсь предмет – уявний мікрофон. Студенти передаватимуть його один одному, по черзі беручи його.

3. Надавайте слово тільки тому, хто тримає в руці уявний мікрофон.

4. Запропонуйте студентам говорити лаконічно і швидко.

Правила для студентів.

1. Говорить тільки той, у кого в руці уявний мікрофон.

2. Під час відповіді одного, інші слухають мовчки, не перебивають і не

вигукують з місця.

Запитання

1. Що називають функцією?

Функцією називають таку відповідність між змінними х і у, при якій кожному  значенню змінної х відповідає єдине значення змінної у. При цьому змінну х називають незалежною змінною або аргументом, а змінну у – залежною змінною або функцією (від аргументу х).

2. Які ви знаєте способи задания функції?

Задавати функції можна формулами, таблицями, графіком, описом.

3.  Що називають областю визначення функції?

Усі значення, яких набуває незалежна змінна (аргумент), утворюють область визначення функції і позначаються D(f) або D(у).

4.  Що називають областю значення функції?

Усі  значення,  яких  набуває  залежна змінна (функція), утворюють область значень функції і позначаються E(f) або Е(у).

5.  Що називається графіком функції?

Графіком функції називається фігура, яка складається з усіх точок координатної площини, абсциси  яких  дорівнюють  значенню аргументу,  а ординати - відповідним значенням функції.

6. Перед студентами вивішують таблиці або демонструють за допомогою мультимедійної системи:

-  формула, якою задається функція;

-  графік функції;

-  назва функції;

-  назва графіка функції;

-  область визначення функції;

-  множина значень функції.

І. Формула, якою задається   

функція

1. у=kx, k>0.

2. у=kx, k<0.

3. у=kx, k<0.

4. y=, k>0.

5. , k<0.

6. y=kx+b, k>0, b>0.

7. y=kx+b, k>0, b<0.      ІІ. Графік функції

8. y=kx+b, k<0, b>0.

9. y=kx+b, k<0, b<0.

10. y=x²

11. y=x³

12. y =√x

ІІІ. Назва функції

1. Лінійна.

2. Квадратична.

3. Прямо пропорційна залежність.

4. Обернено пропорційна залежність.

5. Кубічна.

6. Немає спеціальної назви.

 

ІV. Назва графіка функції   V. Область визначення функції

1. Пряма.     1. (

2. Гіпербола.     2. [0;

3. Квадратична парабола.  3. (-

4. Кубічна парабола.   ІV. Множина значень функції

5. Вітка параболи.    1. (

2. [0;

3. (-

Тоді пропоную студентам записати інформацію про функцію до таблиці, виконаної за таким зразком (таблиця приготовлена  на  дошці  заздалегідь).

Формула, якою задається функція	Графік функції	Назва функції	Назва графіка функції	Область визначення функції	Множина значень функції
1	4	3	1	1	1
2	6	3	1	1	1
3	9	4	2	3	3
4	2	4	2	3	3
5	11	1	1	1	1
6	7	1	1	1	1
7	3	1	1	1	1
8	10	1	1	1	1
9	8	2	3	1	2
10	1	5	4	1	1
11	5	6	5	2	2

7.  Ви вже визначили яку функцію задає кожний із зображених графіків.

Подумайте, які явища природи і фізичні процеси можна описати з їх допомогою.

Відповіді. 1) у=kx

- залежність між шляхом S, пройденим тілом при сталій швидкості V і часом t його руху.

S=V·t.

- між потужністю струму Р і його силою І при сталій напрузі U.

Р= ІU.

- закон Ома U=RI.

2)

- залежність струму від опору

- залежність тиску від об'єму - закон Бойля-Маріотта

3) y=x²

- залежність кінетичної енергії від швидкості ,

- залежність пройденого тілом шляху від часу при вільному падінні

4) y=x³

- залежність об'єму куба від довжини його ребра V

5) y =

- залежність періоду малих коливань математичного маятника від його

довжини ;

6) y=kx+b

- теплове розширення тіл l =l₀(1+α·t);

- залежність питомого електричного опору металів від температури

= (1+ αt).

Сторінка третя.

«Лічи швидко»

Вправи 1, 2 можна розв'язати усно з обґрунтуванням відповіді.

1. Функція задана формулою.

Чи проходить графік функції через дану току:

а) y=4x-5, A(3;6)   б) y=-3x, B(2:-2)

Розв'язання

6=12-5     -2=4-6

6≠7     -2=-2

Графік функції            Графік функції

не проходить             проходить

через А (3;6)               через В(2;-2)

2. Два студенти розв’язують на відкидних дошках, а всі інші самостійно, потім звіряють результати.

Функція задана формулою f(х)=6х-1. Знайти значення х, при яких х:

а) f(x)=11:  б) f(x)>-19

Розв'язання

6x-1=11 6x-1>-19

х=12  6x>-18

   x>-3.

Відповідь. х=12; x>-3.

3. Знайти область визначення функції : 1) y=; 2) ;

3) .

Студенти розв'язують на дошці під керівництвом викладача.

Розв’язання

1) y=

x-8≥0

x≥8

Відповідь. D(y)=[8;

2)

Відповідь. D(y)=(-

3)

Область визначення функції утворюють ті значення х, при яких вираз 3х+2 набуває додатних значень, в вираз - 3 відмінний від нуля.

Тому потрібно розв'язати систему

 

                -3             3            x

Відповідь. D(y)=(

Сторінка четверта

«Будуй точно»

1) Виконується за вказівками викладача

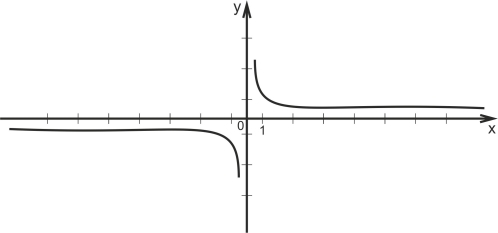
Побудуйте графік функції

а)

Розв’язання.

Знайдемо область визначення функції

x²-6x≠0

x(x-6)≠0

x≠0 x≠6

D(y)=(-

Отже, графіком даної функції буде гіпербола без точки (6;

x	-8	-6		-2	-1	1	2	4	6	8
8y					-1	1

 

б) y= де х≥0

D(y)=[0;

y=

x	0	1
y	0	-2

 

 

 

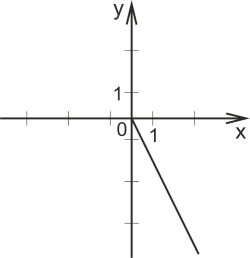
Деякі процеси відбуваються так, що їх можна описати функцією заданою різними формулами на різних проміжках.

3. Колективно будуємо графіки, розв'язуємо рівняння.

Дано функцію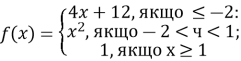

а) Побудуйте графік цієї функції

б) Розв'яжіть рівняння f(x)=2

Розв’язання

Щоб  побудувати  графік  такої  функції,  досить  на  проміжку (-;-2] побудувати графік функції у=4х+12, на проміжку (-2; 1) - графік функції у=х² і на проміжку [1; ) - графік функції у=1.

 

у=4х+12         у=х²                  у=1

x	-3	2		х	-1	0
y	0	4		у	1	0

 

 

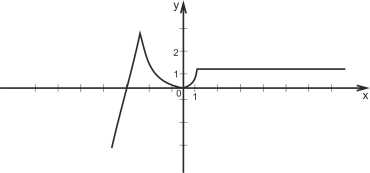
б) Якщо f(х)=2, то  

Відповідь: -2.5; .

IV. Підсумок заняття

Ось ми і перегорнули останню сторінку нашого журналу. Сподіваюся, що ви, готуючись до цього заняття, систематизували та поповнили свої знання про функцію,  області визначення і  значень  функції, графіки раніше  вивчених функцій. (Викладач характеризує  знання студентів, повідомляє оцінки їм за відповіді і виконані завдання).

V. Домашнє завдання.

За підручником [1] Розділ1 §4 №161, 164, 178.